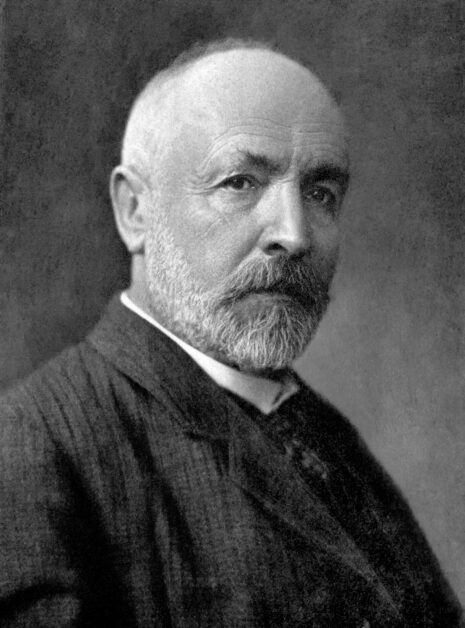搞懂「通用圖靈機」的第一站——康托爾的「無限樂園」 │《電腦簡史》數位時代(十二)
本文為系列文章,上一篇請見: 現代電腦從此展開——馮紐曼與馮紐曼架構 │《電腦簡史》數位時代(十一)
數學能不能判定?圖靈機的源起
在美國那些電腦先驅著手設計電腦之前,英國劍橋大學有位研究所新生已經發表論文,率先指出通用型電腦的可能性。這位學生就是後來有「電腦之父」、「人工智慧之父」等美譽,還在二戰期間發明電腦破解德軍密碼的天才——圖靈。
圖靈撰寫那篇論文的初衷極為特殊,與實際計算毫無關聯。之前介紹過的那些電腦先驅,若不是因為在就學期間經歷計算之苦,就是工作上遇到瓶頸,才會一頭栽入計算機的研究,希望透過機械化與自動化讓計算更快速、更準確。但圖靈都沒遇到這些狀況,他也沒想要解決實務上的技術問題。事實上,他的論文根本無關乎計算,而是要回答一個極為抽象的大哉問:數學是否可以判定?
什麼叫可以判定?這與計算機有什麼關係?要說清楚這來龍去脈,也為了搞懂圖靈所設想出來的通用圖靈機是什麼,得先探究另一個數學問題——「無限」。
無限是什麼?康托爾挑戰數學界千年共識
從亞里斯多德以降,無限向來被視為一種潛無限 (potential infinity),是進行中的未完成狀態,不能當成實體看待,更不能比較大小,否則就會出現矛盾。
例如伽利略便曾舉出一個悖論:自然數 (1、2、3、……) 與平方數 (1、4、9、……) 哪個比較多?照理說自然數當然遠比平方數還多,可是如果用一個蘿蔔一個坑來想的話,每個自然數都有個平方數與之對應 (1🡪12 、2🡪22 、3🡪32 、……),表示有多少自然數,就有多少平方數,兩者一樣多,這不就前後矛盾了嗎?因此伽利略主張等於、大於、小於這些關係不能應用於無限。數學王子高斯也嚴正表示:「我反對將無限量看成真實的實體來運用,這在數學之中是永遠不被允許的。無限只是一種說法而已。 」這句話可以說代表了所有數學家的共同看法。
沒想到 1874 年,不到 30 歲的德國數學家康托爾 (Georg Cantor) 竟然跳出來說:不對,無限大可以當成實體做比較,而且可區分大小,例如實數的集合就比自然數的集合大!
康托爾當然有所本才敢公然挑戰數學界長久以來的信念,不過他所提出的證明是用集合論的方法,不好解釋,我們改用他後來在 1891 年提出的「對角線法 」來做說明。這不只是因為這個方法更簡潔易懂,更因為它影響深遠,啟發圖靈解決了判定問題,也才誕生出極具開創意義的「通用圖靈機」。
德國數學家康托爾 (Georg Cantor,1845-1918)。圖:Wikipedia 騙肖ㄟ,有理數和自然數一樣多?
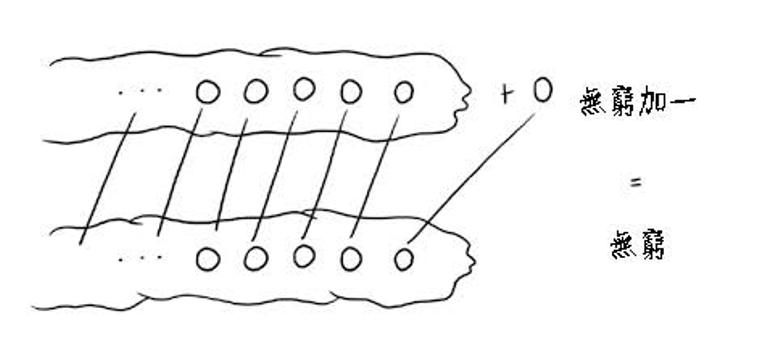
首先讓我們重溫一下怎麼比較集合的大小。基本上只要集合所含的元素一樣多,它們就是一樣大,例如A={1,2,3},B={2,4,6},兩者的元素都是 3 個,所以 A 與 B 大小相等。問題是無限數列沒有止盡,要怎麼數有幾個?沒關係,同樣用一個蘿蔔一個坑的概念,只要兩個集合的元素彼此一一對應,就代表這兩個集合大小相等。所以按照這個定義,伽利略悖論就解決了:自然數的集合與平方數的集合一樣大。
那麼自然數與有理數呢?可以用分數表示的數就是有理數,而光在 0 和 1 之間就有無限個分數,當然是有理數遠多於自然數啊!等等,且看康托爾怎麼巧妙地列出所有有理數:
1/1
1/2、2/1
1/3、2/2、3/1
1/4、2/3、3/2、4/1
…………以此類推
第一行是分子與分母相加為 2 的有理數,第二行是分子與分母相加為 3 的有理數,第三行相加為 4、第四行相加為 5,……以此類推,便可以列出全部的有理數,一個都不漏。然後我們再由上往下,一行一行的由左向右依序為每個有理數編號:1、2、3、4、……,如此一來,有理數不就與自然數一一對應了嗎?所以有理數的集合與自然數的集合也是一樣大。(如果要涵蓋負的有理數,只要依樣放在這個三角形列表的右半部就行了)
到目前為止,我們看到自然數、平方數、有理數這些集合,雖然乍看明明大小不同,結果卻證明無限是不分軒輊的。那麼同樣是無限多的實數,憑什麼就比它們都來得大呢?
比無限大還大?康托爾祭出對角線法
實數除了有理數,還包括無理數,也就是無法用分數表示的數,例如 \(\sqrt{2}\)、π、……等等,所以我們得用小數來列舉實數。先來看 0 與 1 之間的所有實數,也就是純小數。絕大部分的數字小數點後有無限多位數,所以沒辦法像有理數那樣依序一一列舉,不過沒關係,我們就不按大小順序而是任意列舉,例如:
0.5 41592653…… 0.04 1719652…… 0.862 235975…… 0.6401 94231…… 0.23417 8276…… ……
反正我們姑且假設所有純小數都在這張無限長的表格裡了,因此都有個自然數與它對應。現在對角線法要上場了。我們從第一行取小數點後第一個位數,第二行取第二位數,以此類推,可以得到一個小數:0.54217……。然後我們將每個位數都加上 1,會得到一個新的小數:0.65328……。
這個新的小數很特別喔,因為它和每一行的數字都有一個位數不符,表示它絕對不在這張表裡面,也就是這個小數沒被自然數對應到,前面假設所有純小數都在這張表並不成立。
你可能會說:那還不簡單,再把這個新的小數加進去這張表就好啦。可是加了之後,我們仍然可以用剛剛的對角線法,又產生一個不在表中的新數字,因此永遠有自然數對應不到的小數,足以證明小數的集合比自然數還要大。
康托爾把自然數、有理數這類可列舉的數稱為「可數無限 」,是最初級的無限,算是第 0 級。小數則是「不可數無限 」,是第 1 級無限,比第 0 級無限還要大(註一)。就這樣,長達兩千年的普遍信念,一夕之間被康托爾徹底顛覆了,無限不再是無從比較的概念,而是可以明確區辨的實體。
現在你知道什麼是對角線法,已經可以直接到下一站,看看圖靈如何構思出計算機。不過康托爾還有許多令人驚奇的把戲,何不繼續往下一探究竟,看看自己有多少錯誤的迷思?
無限的無限的無限……——冪集合的威力
我們已經知道無限有分等級,而純小數的無限等級比自然數或有理數還大。那有比純小數更大的無限嗎?例如 0 到 100 之間的實數?既然實數屬於特殊的不可數無限,不能用前面證明有理數與自然數一樣多的列舉對應方式,那麼範圍更大的實數是不是無限等級就比較大?
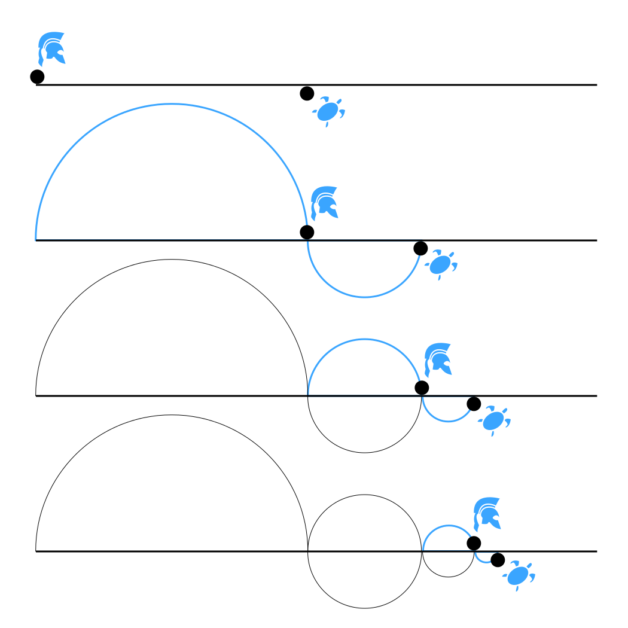
直接宣布答案:不,都一樣大。即使是從負無限大到正無限大,涵蓋所有實數的集合仍然與 0 與 1 之間的純小數一樣大。怎麼證明?如下圖,我們畫一個直徑為 1 的半圓,在它下方畫一條代表往兩端無限延伸的直線。從這條直線上的任一點畫一條線與圓心相連,會與半圓相交於一點。這個點對應到直線上的位置一定會落在 0 與 1 之間,表示任一實數都會有一個純小數與之對應,所以所有實數的集合與純小數的集合一樣大。
講到這裡,你大概會以為無限就分兩種:自然數、有理數這類可數無限屬於第 0 級無限,小數、實數這類不可數無限屬於第 1 級無限。往上不會有更大的無限,畢竟實數都已經涵蓋所有數字了。沒想到康托爾就像魔術師從空無一物的帽子變出兔子般,竟然端出了比第 1 級無限更大的無限:冪集合 。
冪是次方的意思。一個包含 n 個元素的集合,它的子集合個數為 2n ,把這些子集合當成元素全部集合在一起,就成為原來那個集合的冪集合。例如集合 A={1,2,3},那麼 A 的冪集合就是由空集合、{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3},這 8 個集合為元素所構成的集合。
康托爾於 1891 年證明無限集合的冪集合是更大的無限(註二),例如自然數的集合是第 0 級無限,它的冪集合就是第 1 級無限;同理,實數的冪集合則是第 2 級無限。還沒完喔,實數的冪集合又可以組成更大的冪集合(就像上面舉例的 A 集合,它的冪集合的冪集合就有 28 =256 個元素),而誕生出第 3 級無限。
你會想這樣不是沒完沒了嗎?沒錯,新的冪集合不斷衍生,無限的等級也越來越大,永無止盡。
康托爾掀起巨浪,自己卻反遭吞噬
原本一片渾沌的無限,經康托爾大刀一揮,不但有大小之分,而且宛如侏儸紀公園裡的恐龍,一隻比一隻巨大,更可怕的是完全沒有極限。不過康托爾革命性的創見並未獲得當時的主流認同,尤其他的老師公開嚴厲批判,不但造成康托爾謀求教職不順,更重創他的心靈。
1884 年開始,康托爾數度精神崩潰住院治療。出院後他曾一度放棄數學,轉而研究歷史與神學,但後來還是「雖千萬人吾往矣」,繼續打破無限的迷思,發明出影響深遠的對角線法。1900 年代初期,康托爾的研究成果終於逐漸獲得肯定,無奈 1917 年他最後一次進入療養院時,德國因為一次世界大戰戰情吃緊,實施食物配給。康托爾因此營養不良而健康惡化,隔年就在院內過世,享年73歲。
好了,無限樂園的導覽到此告一段落,下一章我們就要介紹圖靈。他的悲慘命運不下於康托爾,也是做出了無與倫比的貢獻,最後卻以悲劇結束一生。
註一:康托爾相信並不存在大小介於第 0 級與第 1 級之間的無限。但這至今仍無法證明,因此稱為「連續統假設」。
註二:康托爾就是為此而發明對角線法。證明方式與前面證明純小數比自然數多的做法類似,先假設冪集合可以與原來的集合完全對應,再證明冪集合中永遠有對應不到的元素,所以冪集合的無限等級又大一級。