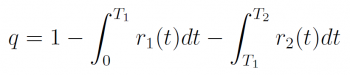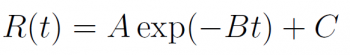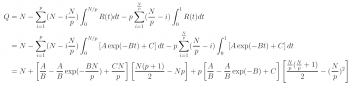我們知道維生素(也稱維他命)在環境中容易被破壞,所以當我們使用維生素藥劑時,可以進行以下策略:把大罐子中一部分的藥劑放入一個小罐子內,先使用小罐子裡的維生素藥劑,等到小罐子吃完後打開大罐子再次把藥劑倒入小罐子內,如此循環。由於大部分的藥劑都存於大罐子內,並且在大部分的時間都處於封閉的情況,因此可以減少氧化的程度。然而,我們可以想像,如果一次倒入小罐的維生素藥劑太少,我們必須不斷地打開大罐子,這時封閉的大罐子的策略就失效了;另一方面,要是倒入小罐的維生素藥劑太多,那大量的維生素在小罐內每天被打開食用,我們想要減少氧化的策略也會施小。因此,今天想研究的就是:要在小罐子裡裝多少藥劑才會有最少的氧化程度?
(% 對於不想看推導公式的朋友們請直接往下跳結論囉! %)
首先,我們把上述問題化成數學問題:想像一個人購買了一大罐,裝了 N 顆的維生素藥劑,每天吃一顆,N 天會吃完。為了減少氧化程度,我們把維生素分成了 p 次裝入小罐中,也就是說,第一步,打開大罐子,把 N/p 的藥劑放入一個小罐子,之後 N/p 天都使用小罐子中的藥劑,等小罐子中藥劑使用完畢再度打開大罐子倒入 N/p 顆維生素,如此循環。為了研究這個問題,我們定義單顆維生素的品質為 q(t),他的值在一開始剛買到的時候是 1,在氧化的過程中慢慢往 0 的方向減少;除此之外再定義一個品質下降速率 R(t),可用於計算此單顆藥劑被食用時的品質了。我們可以寫下此單顆維生素被食用時的品質:
其中 r1、r2 為大、小罐子氧化速率隨時間的變化 ;T1 是此藥劑從大罐子轉移至小罐子的時刻,T2 則是此藥劑被服下的時刻。
我們也可以計算所有維生素藥劑被食用時的品質總和 Q。當我們剛買來整罐的維生素時,維生素藥劑的品質總和為 N (normalized 之後的值,單顆藥劑品質一開始為 1),而我們想知道的問題是,要使用什麼樣的 p 值才可以最大化 Q 函數。很顯然這個問題的答案是決定於品質下降速率函數 R(t),當 R(t) 決定之後,Q 可以藉由許多的積分和總和來決定,而最佳的 p 值則可由 Q 對 p 微分來得到。這個函數和研究也可用在一些相似的衰減(decay)系統。下面讓我們來猜猜品質下降速率 R(t) 並且試著研究最佳化的裝罐策略吧!
1. 近似方法
1-1 近似一
想像開罐的時候,空氣會進入罐中,那些會氧化維生素藥劑的東西會補充,達到常溫常壓下的一般環境濃度;蓋子關上後,這些東西的數量會慢慢下降。因此,R(t) 函數應該和距離上一次開罐之間的時間有關,因此,假設 R(t) 函數是通用(universal)函數,在所有的罐子中都是一樣的函數,也和罐中狀況無關聯,只和距離上一次開罐之間的時間 t 有關。
1-2 近似二
氧化速率 R(t) 隨時間t的變化可以從化學反應速率以及瓶中氧化物質減少速率,瓶外空氣滲入瓶中的量等等因素決定。然而,在此假設 R(t) 是 exponential decay 函數,並且令 R(t) 在 t = 0 時有最大值,接著快速衰減;由於罐子不是密封的,因此會有少量空氣緩慢地滲入補充罐子內部氧化物質,因此可以推論此decay函數最終最小值為一大於零的數:
其中 t 是距離開罐之間的時間(請見近似一說明),A、B、C 為決定此 decay 函數的參數 (皆 > 0)。其中,B 為 decay 速度的參數,單位為時間的倒數 (1/t)。C 則為 R(t) 的最小值,A 為 exponential 函數的震幅。有了 decay 函數 R(t),我們就可以推導這一罐維生素藥劑在不同 p 值的策略下,使用的品質總和:
最終的形式顯然看起來非常複雜。下面就來討論 R(t) 函數的參數如何改變最終的結果。
2. 討論
2-1 B 參數的設定
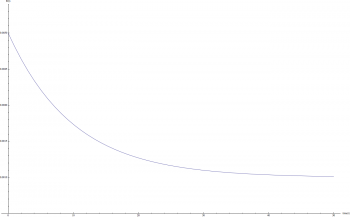
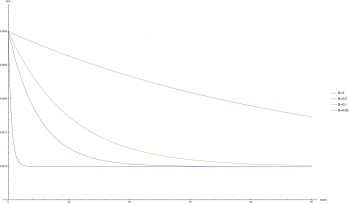
因為 B 參數是和時間有關,而不是和品質,數量有關的參數,因此相對好處理。下圖顯示不同 B 參數下 R(t) 的變化:
(藍: B = 2; 紅: B = 0.2; 黃: B = 0.1; 綠: B = 0.02)
可以發現當 B 的值較大時 R(t) 函數下降速度較快。或許我們可以合理的猜測,在實際的狀況中,當 t = 20 天的時候,R(t) 函數會趨近於最終值:R(20) ~= C;因此,在這次的計算中 B = 0.2。
2-2 A、C 參數的設定
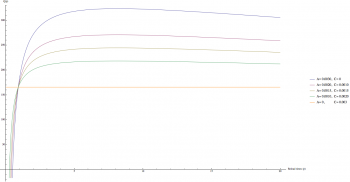
A、C 參數的設定就比較困難了。一個可能合理的猜測是,維生素廠商並不能假設維生素藥劑使用者會把藥劑裝到小罐子中避免氧化,因此在使用期限內維生素的品質必須要維持在一個看似合理的數值,因此,我們可以推測,在沒有使用 “裝到小罐子中儲存” 策略的情況下 (p = 1),最終服下維生素藥劑的品質 Q 應該要是一個看似合理的數值,譬如說 Q (p = 1) = 0.5 N。這個假設當然很有可能和事實有出入,譬如說,合理的數值可能更多可能更少;然而,A、C 的絕對值對於最佳化p的值並不會有很大的影響,而是 A 和 C 的比值影響比較大。我們試著帶入 N = 365 (一年的維生素藥劑),並且引入剛剛所說的條件 Q (p = 1) = 0.5*N ~= 182,可以得到 A + C 約等於 0.003。下圖畫出不同的 A、C 比值得到的 Q 隨 p 變化曲線。
(藍: A = 0.003, C = 0; 紅: A = 0.002, C = 0.001; 黃: A = 0.0015, C = 0.0015; 綠: A = 0.001, C = 0.002; 橘: A = 0, C = 0.003)
首先發現所有曲線都通過一接近 p = 1 的點 (此交點 p != 1),當不使用分罐策略時會有相似的品質。接著,我們也可以發現當 C 遠大於 A 時 (exponential term 消失,速率函數變成線性,此時和開關罐子無關,因此分裝行為變得沒有幫助),Q 變成一條直線,顯示 Q 並不隨 p 的值變化。當 A 的值越來越大 C 的值越來越小,會發現曲線變得越來越圓滑,最終當 C= 0 時達到最圓滑的曲線。
3. 結論
從上面的討論可以得知:
(1) 若是氧化的速率不會隨開瓶關瓶變化,那分裝策略沒有幫助。
(2) 大致上來說,最佳的分裝策略的 p 值分布在 5 ~ 10 之間,也就是假如買了一罐一年份 365 顆維生素,一次裝入小罐子的量大約是在 40 ~ 80 顆之間。不過大部分曲線在 p > 10 之後仍然有不錯的值,因此更少的顆數 (< 40) 是可以接受的。
(3) 分裝策略能夠增加 20% ~ 70% 的維生素藥劑新鮮度,不過由於 A、C 的絕對值不是非常精確,因此實際增加的量還需要更詳細的研究。
致謝
感謝室友楊智軒 (Louis Yang) 在討論中提出的許多有用的建議。