要怎麼多吃一點冰淇淋 －從賽局理論與實驗經濟學談連續議價賽局

圖片來源：picjumbo Sunny Ice Cream By Viktor Hanacek

作者：謝沛勳｜國立台灣大學經濟學研究所

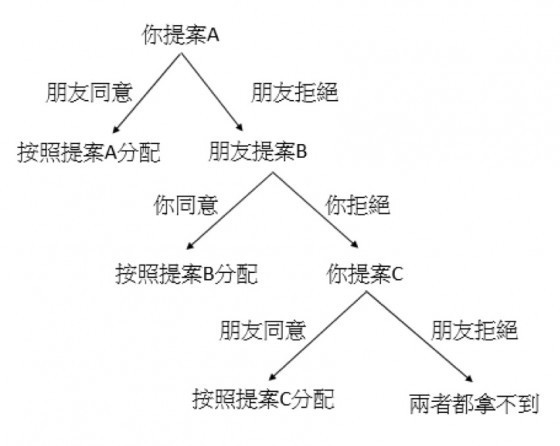
在8月的中午，你跟朋友路過全家，抽獎抽到了一根冰淇淋。在炎炎夏日，你們都想多吃一點冰淇淋，因此你們想到一個文明的辦法來分配冰淇淋。你們說好由你先提案決定分配的大小（因為是你提議要抽獎的），你朋友決定是否要接受提案，若朋友拒絕則輪到朋友提案。在38度C的午後，冰淇淋融化得很快，每經過一次提案冰淇淋就融化掉一半，在第三回合後冰淇淋就沒了。也就是說，在第一回合你們有一份冰淇淋可以分，由你來提議各拿多少，若你朋友答應則按照這樣分配，若你朋友拒絕則進入第二回合。在第二回合，冰淇淋只剩一半，由你朋友來分配，如果你又拒絕則進入第三回合。第三回合時冰淇淋只剩四分之一，若朋友還是拒絕則雙方什麼都拿不到。這個時候，你該怎麼分配冰淇淋呢？

今天如果你是故事中的主角，你在第一回合會提議分配多少給朋友呢？如果你跟你的朋友都是一個只在乎看的到的利益（也就是說沒有心理感受）、且完全理性而且又十足聰明的人，應該會這樣想：因為在最後一回合你可以拿到剩下全部的四分之一冰淇淋（只要分給朋友一小小口她就會同意，因為拒絕的話就什麼都沒有，聊勝於無），因此你朋友在第二回合至少得分給你四分之一你才會同意（因為你這回合拒絕的話，下回合也可以拿四分之一），因此他會提議分四分之一給你，自己拿四分之一。既然你朋友在第二回合可以拿到四分之一，在第一回合時你也得分四分之一給你朋友爭取他的同意，自己拿四分之三，這就是賽局理論中的逆向推導法（backward induction）。

看到這邊，你可能會有兩個想法。一是原來要這樣想啊，我好像都沒想到呢，就很直覺得想說要分一部分的冰淇淋給朋友。你也有可能會想說，何必這麼計較呢？應該多分一點給他，不管是不是朋友。的確，在實驗經濟學家作的實驗中，大多數第一回合的提案都介在四分之一到一半之間。原因有二，一個是由於逆向推導法並不直覺，並非大多數人會想得到的；也有可能認為並不需要為了這樣的事情耗費太多腦力。第二則是社會偏好，也就是說人會在乎公平，或擔心對方會在乎公平，一氣之下寧可選擇玉石俱焚也不要冰淇淋了。這在獨裁者賽局（dictator game）或最後通牒賽局（ultimatum game）都能觀察到這樣的現象，《 贏家的詛咒》（Richard Thaler，經濟新潮社，2009）或《金錢實驗室的人性考驗》（陳其一，財信出版，2011）內有詳述。

為了確定這兩個因素在人們決策中的作用，Johnson、Camerer和Sen在2002年做了一個有趣的實驗。實驗的第一部分是給受試者作連續議價賽局（sequential bargaining game），也就是上述分冰淇淋的賽局，但是此處用5塊美金代替，且受試者在實驗中所獲得的報酬結束後可以拿回家（經濟學家很重視實驗中有真實的誘因，缺錢的人快去找徵求受試者的廣告！）。這個實驗是利用電腦進行的，電腦隨機幫受試者兩兩配對，受試者知道對手也是一樣在實驗室的，但不知道對方是誰也不可以交談，且每回合會重新配對。受試者會看到以下畫面。

圖片來源：E.Johnson,C.Camerer,S.Sen,"Detecting Failures of Backward Induction: Monitoring Information Search in Sequential Bargaining",2002,Journal of Economic Theory

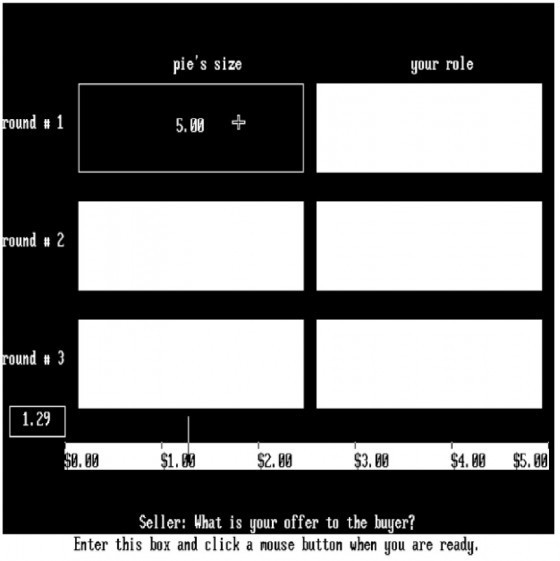
關於每回合可以分配的報酬是隱藏在盒子後面的，要用滑鼠點擊才看得到。其中pie’s size指的就是這一回合可以分配的金額，左邊的數字指的是第幾回合。下方的數字Bar則是給受試者選擇要分配多少金額。而電腦會記錄受試者點集盒子的次數、時間與順序。Johnson等人發現有很大一部分的受試者甚至連第三回合還剩多少報酬都不知道就做決策，絕大多數的受試者取得資訊的方式也是從第一回合開始，可見絕大多數的受試者並沒有使用逆向推導法。因此提出了有限認知理論取代之：有限認知的模型假設如果受試者只看第一回合的報酬，受試者便會把這個賽局當作最後通牒賽局（註一），並且分給對手40%（2元）的報酬，稱此類的受試者叫Level 0。若這個受試者看兩回合的報酬，則會認為對方在第二回合會分給他40%（1元）的報酬，自己留60%也就是1.5元，因此在第一回合會分給對方1.5元，稱此類的受試者叫Level 1。實驗結果發現，提議給對手1.5元到2元之間的人，的確比提議給對手2元以上的人多看了很多次第二回合的盒子！而在實驗中平均第一回合的提案金額則是2.11美金（賽局理論的均衡是1.25美金）。

第二部分則是告訴受試者他們的對手是只在乎自己利益，而且絕對理性的電腦。因為對手不是真人，受試者不會考慮公平的問題，可以用這個方法來拿掉受試者的社會偏好。結果發現受試者的提案金額的確降低了，第一回合的平均提案金額從2.11美金降為1.84美金，少掉的這部分就是社會偏好的影響。但是距離賽局理論的均衡（1.25美金）仍然有很大一段距離。

所以，在炎炎夏日吃冰淇淋時，別忘了看一下實驗經濟學的書吧。可以看Kahneman的《快思慢想》，有經濟學底子的可以看Thaler《贏家的詛咒》，一起來領略實驗經濟學的趣味吧！

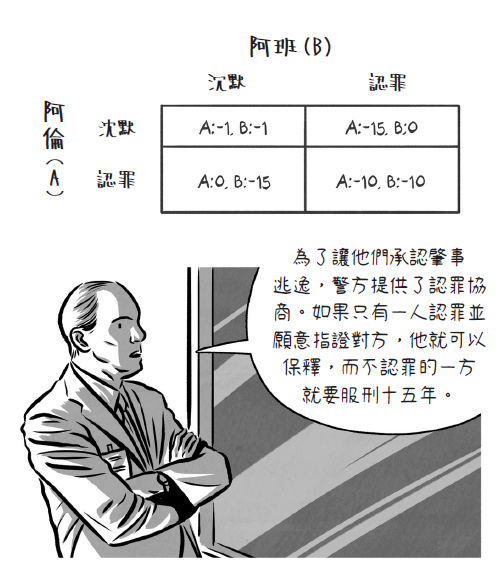
註一：最後通牒賽局（ultimatum game），提案者可決定如何分配一筆報酬，若對方接受則按照提案分配，若拒絕則兩者都拿不到任何報酬。以分配十元為例，賽局理論認為分一元給對手且對手會接受，因為拿到一元總比拒絕提案沒拿到任何報酬好。但實驗中受試者平均的提案是分40%給對手。

參考文獻：E.Johnson,C.Camerer,S.Sen,"Detecting Failures of Backward Induction: Monitoring Information Search in Sequential Bargaining",2002,Journal of Economic Theory

延伸閱讀

• 賽局理論與公投門檻
• 電影【史密斯任務】中婚姻的囚徒
• 葉丙成：修課如遊戲？台大電機這麼教！