
麥卡托一五六九年那幅著名的地圖,究竟有什麼好的呢?它充滿了失真變形,一大堆國家都比實際上大上許多倍。而更令人驚訝的是,它基本上仍是現今我們所使用的地圖。當然我們在地圖上添加了國家,海岸與疆界的模樣也經過校正以及政治修正,不過這幅地圖描繪了文藝復興尾聲時的模樣,見證了啟蒙時期,也裝飾在維多利亞時期課堂裡,一直為人們所選用,並沿續至今最新的Google Maps裡。它是我們這個世界的限定符號,若是妄然更動它,彷彿就像是恐怖主義行動一樣。人們可不是沒有嘗試過。
當然,我們所凝視的不是一幅地圖,而是這個世界的投影——是所有地圖的模板。對傑拉德.麥卡托來說,或許有一些諷刺,他出生於比利時的法蘭德斯(Flanders),在萊茵河畔的杜伊斯堡(Duisburg)工作,當時並不是什麼多產的製圖師。當他於一五六九年發表了他名聞遐邇的世界投影法,時值他五十七歲,他也不過繪製了不到十幅的地圖。不過他的這幅新作毫無疑問是個驚奇——精密的數學基礎,輔以驚人的尺寸與雄心壯志。這幅地圖粗估為兩公尺乘以一點二五公尺,橫跨十八張印刷紙,能震懾每一個看見它的人。
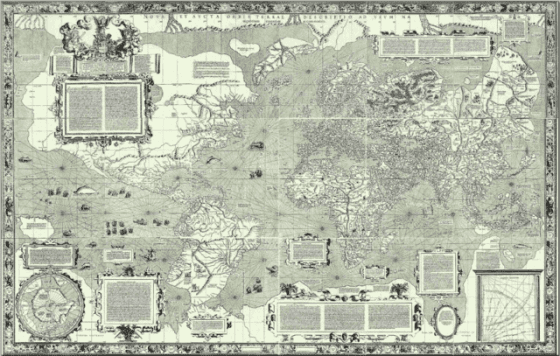
地圖上以現代眼光看起來錯誤的地方——格陵蘭島與澳洲一樣大而不是只有三分之一;一塊南極大陸沿著底部出現,既粗略又難以界定——並不是最怪異的部分,因為確切的比例大小還不為人知,而極地區域仍是無解的謎思。對於麥卡托同世代的人們來說,最怪異的事情是麥卡托這個人從未到過海上(將來也不會),卻能如此有效地幫助水手們擺脫數世紀以來所憑靠的直覺,測定出橫渡不同海洋的航線。陸軍也必須對他表示感謝:他幫助他們能更準確地發射大砲。
麥卡托地圖的主要貢獻是技術上的:自從世界被認為是個球體開始——一般認為這個說法起自亞里斯多德——有個難題一直困擾著製圖師,而麥卡托地圖則提供了一個解決之道。這個難題是:如何在平面圖上呈現地球的弧形表面?嚴謹且發展完善的經緯線對於理論上的座標來說非常適用,但是追求著穩定不變航線的航海家是航行在一個無止盡的弧線之上。麥卡托已經利用恆向線在他的地球儀上呈現出彎曲的路線,現在他想要將這些轉移至地圖上,使任何航海家都能迅速定位自己所在位置,找到前往任何目的地的航線。
麥卡托與這個難題糾纏了好一會兒。你也可以自己試試看:拿一顆毛茸茸的網球,在上面畫一些代表國家的形狀,然後將它切成兩半;在切面上劃幾刀,將之展平。這些國家會凸起在中間,為了讓這個網球地圖可以攤平,中間便會縮小而邊緣會被擴張。現在試著更精確一點來處理,好讓水手們能帶著貨物回家。麥卡托所追求的就是利用數學算式來找到處理這個難題的方式。
麥卡托於一五四六年寫給一位朋友的信中提到,同樣一趟海上航程經常在不同船上的航海日誌裡記錄著迥然不同的緯度。地圖完全是誤導人:「我看到所有的航海圖⋯⋯都無法達到本來的目的。」他不是第一個發現這件事的人,不過這個問題一直到十六世紀才完全浮現,當時羅盤益發精良,經典的發現之旅帶領船隻航向新的海洋。在當時短短數十年間,各式各樣嶄新且經常是怪異的投影法出現了:方位角(Azimuthal)與方位投影(Azimuthal Equidistant)、正射切面投影(Orthographic)、球心切面投影(Gnomic)、球面透視切面投影(Stereographic)、心狀投影(Cordiform)、擬心狀投影(Pseudocordiform)、球狀投影(Globular)、梯形投影(Trapezoidal)以及橢圓形投影(Oval)。
幾乎上述所有投影方式都仰賴於經緯度的座標系統,大多數都標記出熱帶地區與赤道。這些投影方式不全都是為了航海所設計,有些較適合用於天空或是極地區域的地圖繪製,而也有些適合用於說明或是表達概念。達文西(Leonardo da Vinci)與杜勒¹(Albrecht Durer)也針對這個問題提出他們藝術家的看法。
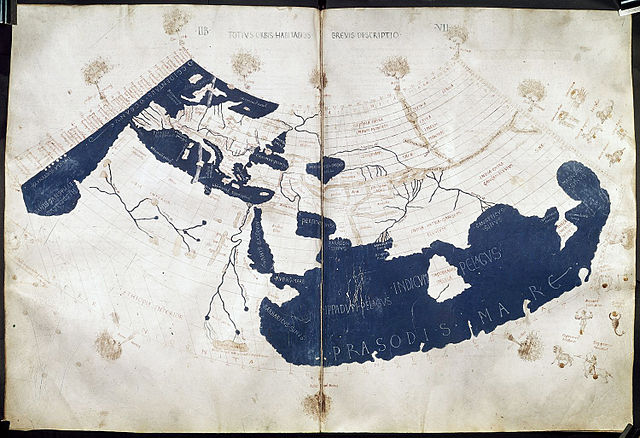
無可避免地,托勒密也已經首先處理過這個議題——兩次。他稱某個投影法是「較差但較簡單的」,還有一個則是「較好但較麻煩的」。前者,即他現在被認可為經典的座標系統,在先天上有其侷限:舉例來說,在這種最初的投影法裡,他的緯度起始自赤道(南緯16.25度至北緯63度之間),而經度僅僅延伸至180度,零度的子午線起始自福島(Blessed Isles),現在被認為是西班牙的加那利群島(Canary Islands)或非洲西岸的維德角群島。儘管如此,考量到座標系統的不足所帶來的種種侷限,托勒密投影法所涵蓋的區域,在國與國之間的相對位置上已經可說是與我們現今所認知的相當近似了。
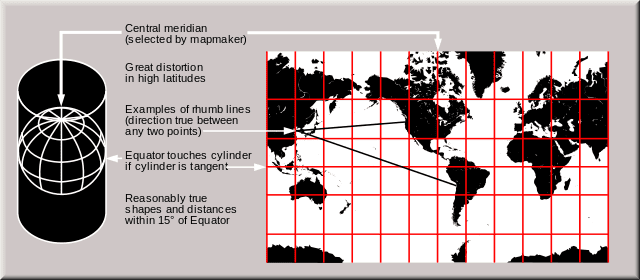
麥卡托極為仰賴托勒密的地名辭典,輔以近期的地理發現加以更新,尤其是北美形狀已徹底為人所知,可說是圓滾滾的。但是他歷久不衰的創舉則是他新的正形投影(Conformal projection),他巧妙地調整緯度,使所有角度成直線(緯線離赤道越遠則越彼此分離)。水手們因此可以悠遊於地圖上的直線之間,保持住他們閃動不止的羅盤所指出的前進方向。 麥卡托利用北美尚無人探險的內陸以及空蕩海洋上的空白處,向那些不熟悉這個新投影法的人們證明它的合理性。他解釋道他意圖「將球體表面攤開在平面上,使各個地區的相對位置彼此之間皆正確,連同距離以及經緯度也考慮在內。」如此一來,麥卡托創造的這種座標系統,以他近期的傳記作者尼可拉斯.揆恩(Nicholas Crane)的話來說:「如同哥白尼(Copernicus)的日心說一般雋永。在追尋空間真實的本質上,他成為現代製圖之父。」
1. 杜勒(Albrecht Durer,1471-1528),德國畫家,被視為北方文藝復興最重要的人物,以木刻版畫最具影響力。

由馬可孛羅文化出版










































