- 作者:陳曦、蘇禹安 / 台北市立大同高級中學
「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2021 數感盃青少年寫作競賽/高中組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。

上高中後,搭乘捷運成為日常生活的一部分,某月初進站時發現悠遊卡多了一百多元, 剛開始以為自己記錯卡片的餘額。但到了下個月初又多了一筆錢,所以去加值卡機查詢儲值紀錄,發現原來是捷運卡的回饋金。
查了台北捷運公司官網資料,現金回饋比例是由上個月累計搭乘次數根據下圖(圖一)的對應方式決定,而回饋金為累積搭乘金額再乘上現金回饋比例,在每個月初會回饋到捷運乘客的悠遊卡。
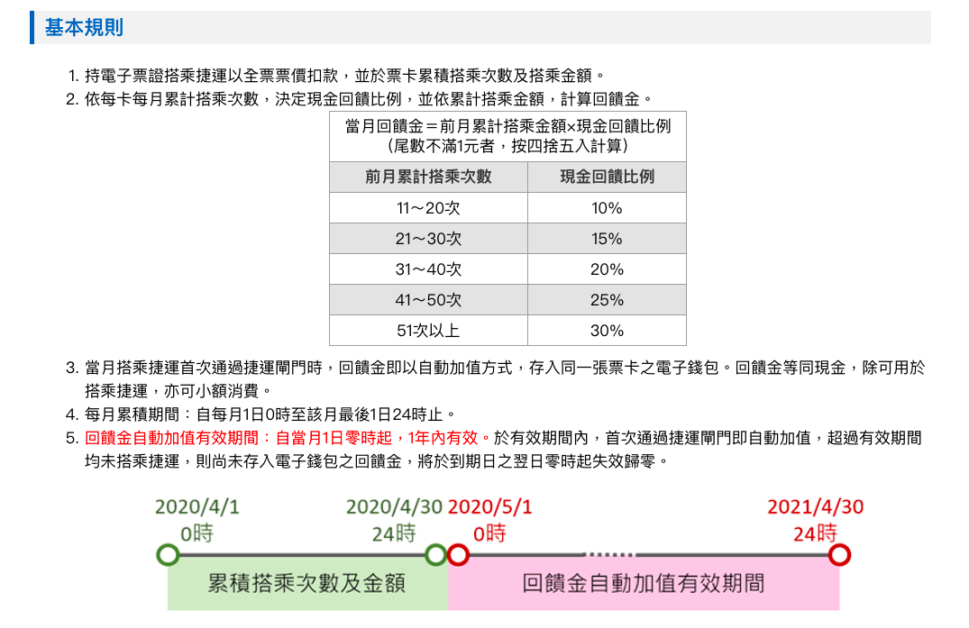
某個月的月底,放學搭捷運回家,進站時我發現這個月恰好乘坐捷運 50 次,差一次就可以在下個月拿到 30% 的現金回饋比例,於是我在途中先出站,再進站搭乘捷運。果不其然,下個月的回饋金就是上個月搭乘金額的三成。
因此我好奇,如果不考慮進出站與等車的時間成本,單純以花費考量,
「把單趟車程分段搭乘來累加搭乘次數,以此獲得更多的現金回饋比例,如此一來我是否能省下搭乘的花費?」
哪些分段方式可以省下通車費用、哪些則不行呢?於是,我們開始了以下研究。
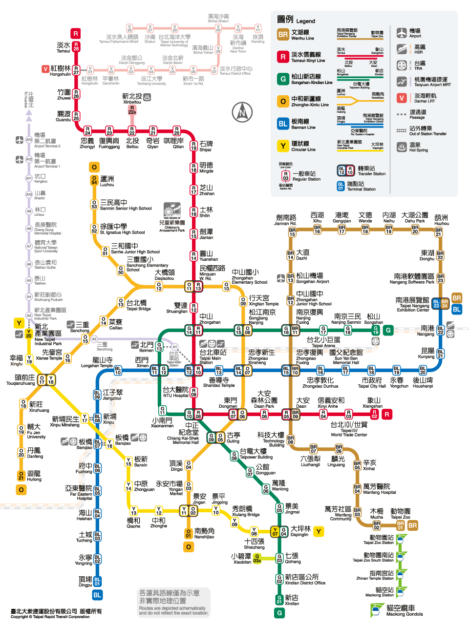
捷運地圖如下圖(圖二),事實上可以分段搭乘的路線不勝枚舉,我們無法一條一條去計算比較哪些路線分段搭乘比較划算。關於如何分段搭乘比較省錢,我們會從「(問題一)拆成幾段搭乘?」、「(問題二)每月搭乘幾次?」、「(問題三)乘坐多少里程數?」等三方面去討論,再利用所學的不等式運算,找出分段搭乘比較省錢的方法,以此判斷哪些路線可以分段搭乘。
首先,我們先探討分段搭乘的票價至少會貴出多少錢?

上圖(圖三)是台北捷運公司官網公告的捷運車票計價方式,是根據起/終點的行車距離計算票價,我們將乘車距離對應的票價整理在下表(表一)。

若今天我們出門需乘坐 24 公里的車程,則票價為 55 元,如果分成兩段 12 公里乘坐的話,票價就變成 35+35=70 元,所以分段搭乘貴了15 元。然而,也可以拆成 5+19 公里來乘坐,則此費用變為 20+45=65 元,僅貴了 10 元。
所以,各個階段的票價,會因為分段搭乘的方式不同而有不同的費用。事實上,我們經過各種拆法的嘗試,在 55 元的票價之下,拆兩段的總票價至少會多出 10 元。上表(表一)是我們整理出來各個票價之下,分拆成兩段與三段搭乘時,要多支付的最小差價以及其分段乘坐的方法。從此表我們可以得出:
- 分成兩段搭乘的話,票價至少要多花 10 元。
- 分成三段搭乘的話,票價至少要多花 20 元。
接下來,將比較分兩段/三段搭乘的現金回饋比例與單趟搭乘的現金回饋比例之間的差異。
根據捷運公司公佈的搭乘次數回饋金比例資料(圖一),我們整理出單趟搭乘與分段搭乘的比較表格,如下表所示:(表二)為拆三段搭乘的比較;(表三)為兩段搭乘的比較。
由下表二、三可知,當每月搭乘次數為 17~20 次時,分拆成三段搭乘與單趟搭乘的現金回饋比例差距最多,高達 20%;而當每月搭乘次數為 26~30 次時,分拆成兩段搭乘與單趟搭乘的現金回饋比例差距最多,最多到 15%。

根據(表二)的結果,我們先討論第一個問題:「在搭捷運時,拆成幾段搭乘可以節省車費?」
假設我們這個月份以 A 票價搭乘 X 次,所累計的現金回饋比例為 α%,則我們可以算出本月的回饋金為 αAX 元,扣除回饋金,本月實際花費為未分段搭乘的花費 = (1 − α)AX 元
若將 X 次的搭乘,每次都分拆成三段來乘坐,每段票價分別為 B、C、D 元,則累計搭乘次數增加為 3X 次,所累計的回饋金比例為 β%,因此本月的回饋金為 β(B + C + D) 元,而且本月實際花費即為分三段搭乘的花費 = (1 − β)(B + C + D)X 元
我們把「未分段搭乘的花費」減去「分三段搭的花費」即是分三段搭乘可省下的錢,然後再除以搭乘次數 X 得:(1 − α)A − (1 − β)(B + C + D) 元,即是「平均每一趟乘搭乘可以省下的花費」。
因為拆三段搭乘票價會至少貴 20 元,即 B + C + D ≥ 20 + A,因此
(1−α)A − (1−β)(B+C+D) ≤ (1−α)A − (1−β)(20+A) = A(β − α) − 20 + 20β
因為票費 A 最多 65 元,回饋金的差 (β-α) 最多為 20%,拆三段的回饋金比例 β 最多為 30%, 所以分三段搭乘平均每趟可省下的錢不會超過下式:
(1 − α)A − (1 − β)(B + C + D) ≤ 65 × 0.2 − 20 + 20 × 0.3 = −1 < 0
可發現分三段省下的金額是負數,即是不管如何拆三段搭乘都不划算。而拆四段以上搭乘的話,每趟會增加更多票價,所以會更加不划算。因此,我們得到第一個小結論,
結論一:「若分成三段以上搭乘,則總花費一定比不分段搭乘的花費更多。」
因為拆三段以上搭乘一定不划算之下,我們考慮是否可以拆兩段乘搭。如同前段的分析, 將 X 次的搭乘,每次都分拆成兩段來搭乘,每段的票價分別為 B、C 元,則累計搭乘次數增加為 2X 次,所累計的回饋金比例為 β%,因此本月的回饋金為 β(B + C) 元,而且本月實際花費即為分兩段搭乘的花費 = (1 − β)(B + C)X 元
把「未分段的花費」減去「分兩段的花費」後再除以搭乘次數 X 可得,分兩段乘坐之下, 平均每一趟乘搭乘可以省下的花費為 (1 − α)A − (1 − β)(B + C) 元
我們先考慮,如果分兩段搭乘的票價會比原來多 15 元以上的情況,即是B + C ≥ 15 + A,則上式可以整理成:
(1 − α)A − (1 − β)(B + C) ≤ (1 − α)A − (1 − β)(15 + A) ≤ A(β − α) − 15 + 15β
同理,因為票價 A ≤ 65 元,回饋金的差 (β-α) ≤ 15%,拆兩段的回饋金比例 β≤30%,所以,如果拆兩段的票價貴 15 元以上的話,兩段搭乘平均每趟可省下的錢不會超過下式:
(1 − α)A − (1 − β)(B + C) ≤ 65 × 0.15 − 15 + 15 × 0.3 = −0.75 < 0
因此,在此情況下,分兩段搭乘也不會划算。所以,我們的第二個小結論:
結論二:「若分兩段搭乘的票價比原本貴 15 元以上,則分段搭乘一定不划算。」
我們的第二個問題:「若分段搭乘,每個月要乘坐幾次才能節省車費?」
根據(表一)所示,拆兩段搭乘票價至少貴 10 元,由上述結論可知,若分段搭乘能夠省下交通費用的路線,則必須選擇拆兩段的票價只貴 10 元的路線,即是 B + C = 10 + A。因此,平均每一趟乘搭乘可以省下的花費,可以改寫成
(1 − α)A − (1 − β)(B + C) = (1 − α)A − (1 − β)(10 + A) = A(β − α) − 10 + 10β
因為票價A ≤ 65元,回饋金的差 (β-α) ≤15%,若回饋金的差 (β-α) 在 10% 以內的話,則拆兩段搭乘平均每趟可省下的錢不會超過下式:
A(β − α) − 10 + 10β ≤ 65 × 0.1 − 10 + 10 × 0.3 = −0.5 < 0
因此如(表三)所示,每月乘坐太少或太多次都讓回饋金的差 (β-α) ≤10%,則拆兩段搭乘不會省下車票花費。唯有在回饋金的差 (β-α) 在最高的 15% 時,也就是每月乘坐次數在 26 次到 30 次之間,拆兩段搭乘的方式才能節省費用。所以,我們的第三個小結論:
結論三:「若拆兩段搭乘的花費能比較少,則每月乘坐次數需介於 26 到 30 次之間。」
最後,我們要討論:「至少乘坐多遠的距離,拆兩段搭乘才能節省費用?」
因為每個月乘坐次數是介於 26 次到 30 次之間,所以單趟搭乘的現金回饋比例為 15%(α=0.15);而拆成兩段搭乘的次數增加為 52 次到 60 次之間,所以回饋比例為 30%(β=0.3)。 由(結論二)可知,拆兩段的路線必須是只能比單趟搭乘多 10 元票價 (B + C = 10 + A),因此平均每一趟乘搭乘可以省下的花費可以表示如下:
(1 − α)A − (1 − β)(B + C)元 = 0.15A − 7 元
如果分段搭乘的方式可以省下費用,則上式要大於零,
0.15A − 7 > 0 → A > 46.6666 …
因此,若拆兩段搭乘能省下費用,則單趟乘坐的票價A要超過 46 元,即是票價 A 為 50、55、 60、65 元。所以,若從里程數來看,我們的第四個小結論:
結論四:「搭乘超過 20 公里的路線,拆成兩段乘坐,才能省下費用。」
因此「什麼路線可以分段搭乘呢?」總結上述討論的四個小結論如下:
- 若分成三段以上搭乘,則總花費一定比不分段搭乘的花費更多。
- 若分成兩段搭乘的票價比原本貴 15 元以上,則分段搭乘一定不划算。
- 若拆成兩段搭乘的花費能比原花費少,則每月乘坐次數須介於 26-30 次之間。
- 搭乘超過 20 公里的路線,拆成兩段乘坐,才能省下費用。
當每個月搭乘次數為 26 到 30 次時,我們歸納出下面此種路線,拆成兩段乘坐可以省下費用:
「該路線票價大於或等於 50 元,並且拆兩段總票價只會多 10 元。」
因此,我們考慮每個月乘坐 30 次,即可算出不同票之下,分段搭乘最多可以省下多少錢,見下表(表四)。所以,在不考慮時間成本下,我們推論出,分段搭乘的方法最多能省下 82.5 元。雖然省下的金額不多,但是推論的過程中,我們發現到有些路線分段搭乘確實比較划算。

最後,根據我們的研究所找到路線選擇的條件,整理出下表這些符合條件的路線以及分段方式,並分成兩種方式呈現。(表五)為淡水信義線範圍內之路線、(表六)是以淡水為目的站之路線,由於數量龐大未能全部列出。不過,下次乘坐捷運時,如果起終點符合上述的條件,不妨試試拆兩段乘坐看看,或許可以幫你在下月獲得更多的回饋金。

資料來源