「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:王姿蘋/景美女中。

教官:「王小明同學,你怎麼老是遲到呢?罰你放學留下來刷廁所!」
小明:「教官,我真的不是故意的,我遲到是有原因的。我已經早十分鐘到捷運站了,卻遲遲上不了車,大家都急著上班上學,每個人看到車門開的瞬間都像猛虎出閘般蜂湧上車,而我又特別瘦弱,根本擠不上車!不如我來分析一篇關於『捷運可以這樣ㄗㄨㄛˋ』的報導給教官聽。」
「嗶嗶嗶!車門即將關閉,請遠離車門。」這樣的台詞在北市的通勤族耳裡再熟悉不過了。在尖峰的上下班時間,常常因為擠不上列車而必須等待下一班。以學生上下學的狀況為例,上學時在捷運車廂最常聽到的是:「不好意思,我快遲到了,可以再往裡面走一點嗎?」不過,當列車開走時,卻發現大部分的乘客都集中在中間車廂,而頭尾車廂的乘客寥寥無幾。 如此貼切的生活經驗,在你我的生活中已習以為常,這樣的情況是否有改變的可能呢?
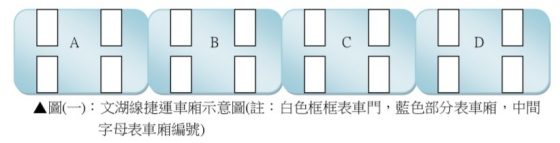
在不考慮中間車廂距離捷運出口較近的因素,且先考慮初發車的車內無乘客的狀態下(即首站),則每節車廂的乘客密度是否能夠趨近平均值呢?以下分為兩點討論:唯一出入口以及為二出入口的情形。以列車車廂相互不連接的文湖線系統來做討論。文湖線的每班列車共四節車廂,而每節車廂同一側各有兩扇車門,如示意圖所示:
討論一:出入口唯一,且位於列車正中間
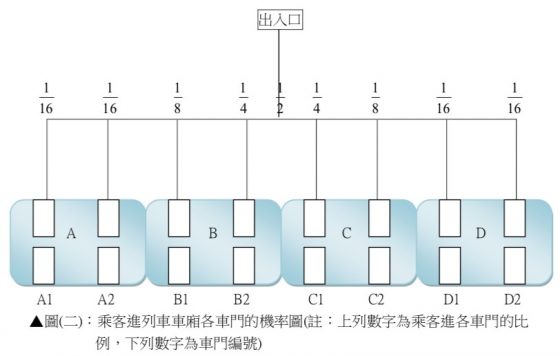
假設出口到車門的距離皆可用直線分割,且每位乘客走到同側各個車門的機率相等,試算首站有 128 位(註一)乘客在同班列車的各節車廂乘客分配,如圖所示:
設首站上車乘客有 a=128 人,則乘客進站後遇到的第一次選擇:往左走或往右走,理想的乘客分布比例為 ⅟2 a 人選擇往左走, ⅟2 a 人選擇往右走。接著繼續直行, ⅟2 a 人遇到 B2(或C1)車門做第二次選擇:進入車門或繼續直行,理想的乘客分布比例為 ⅟2 × ⅟2 a 人選擇進B2(或C1)車門, ⅟2 × ⅟2 a 人選擇繼續直行。以此類推,則 A 車廂的乘客總數為 128× ⅟16 +128× ⅟16 =16人;B 車廂的人數為 128× ⅟8 +128× ⅟4 = 48 人;C 車廂的乘客總數與 B 車廂同為 48 人;D 車廂的乘客總數與 A 車廂同為 16 人。
若每一站下車的乘客數都是各節車廂乘客數的一半,且上車 的乘客數不變,每站同為 128 人(即 A 車廂在第二站下車的乘客為 8 人,上車 16 人),如果這樣計算,平均到了第五站,B、C 兩車廂的乘客數剛好達捷運文湖線每節車廂之上限乘客數 93 人(註二),而 A 車廂及 D 車廂卻只有 41 人,這樣懸殊的比例並不符合經濟效益。如下表所示:
就討論一的捷運出入口設計,我有一個想法想提供給北捷參考:請每站的站務人員安排乘客進入較少乘客的車廂。假設不改變首站的乘客分布比例,從第二站開始,讓 128 位欲上車的乘客皆只能選擇 A 或 D 兩車廂進入,此時各節車廂的理想乘客數分布如下表所示:
接著請第三站的站務人員引導欲上車的 128 乘客選擇進入 B、C 兩車廂;第四站的乘客只能選擇 A 或 D 兩車廂進入⋯⋯交錯車廂上車,以此類推。則各站之各節車廂的理想乘客數分布如下表所示:
如此一來,不但可以減少上下車人潮擠在一起的窘況,也可以讓列車載客量發揮到最大效能,更能避免乘客上不了車的情況發生。
小明:「教官!還有第二個分析,不要睡著囉!」
教官:「這麼有趣的生活數學,我怎麼會睡著呢!」
討論二:出入口唯二,且兩個出入口分別在列車 A、B 車廂中間與 C、D 車廂中間
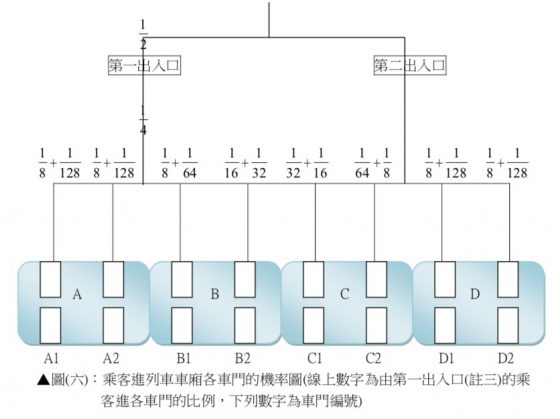
假設出口到車門的距離皆可用直線分割,且每位乘客走到同側各個車門的機率相等,試算首站同樣有 128 位乘客在同班列車的各節車廂乘客分配,如圖所示:
設首站上車乘客有 a =128 人,則乘客進站前遇到的第一次選擇:由第一入口進站或由第二入口進站,理想的乘客分布比例為 ⅟2 a 人選擇由第一入口進站,⅟2 a 人選擇由第二入口進站。
進站後,由第一入口進站的 ⅟2 a 位乘客要做第二次選擇:往左走或往右走,理想的乘客分布 比例為 ⅟2 × ⅟2 a 人選擇往左走, ⅟2 × ⅟2 a 人選擇往右走。接著繼續直行, ⅟2 × ⅟2 a 人遇到 A2(或 B1)車門做第三次選擇:進入車門或繼續直行,理想的乘客分布比例為 ⅟2 × ⅟2 × ⅟2 a 人選擇進 A2(或 B1)車門, ⅟2 × ⅟2 × ⅟2 a 人選擇繼續直行,以此類推其他車門。由第二入口進入的乘客同也。則A車廂的乘客總數為 128 × ⅟8 + 128 × ⅟8 + 128 × ⅟128 + 128 × ⅟128 =34人;B車廂的人數為128 × ⅟8+ 128 × ⅟16 + 128 × ⅟64 + 128 × ⅟32 =30 人;C 車廂的乘客總數與 B 車廂同為 30 人;D 車廂的乘客總數與 A 車廂同為 34 人。
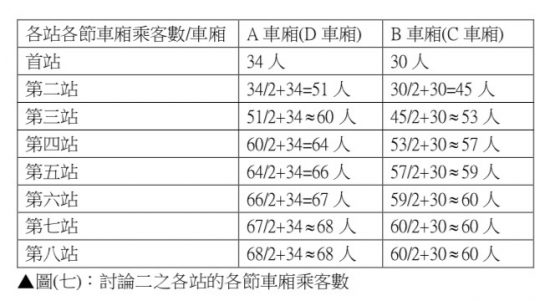
若每一站下車的乘客數都是各節車廂乘客數的一半,且上車的乘客數不變,每站同為 128 人(即 A 車廂在第二站下車的乘客為 17 人,上車 34 人),如果照這樣計算,無論哪一站四節車廂的乘客數皆不會超過捷運文湖線每節車廂之上限乘客數,且每節車廂的乘客數差異不大。另外還有一個驚奇的發現——第六站以後的站別,車廂乘客數將達一穩定值,即進出車廂的人數達平衡,不再改變。如下表所示:
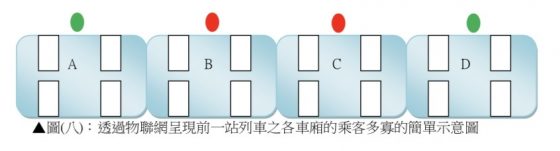
上述的兩個討論皆只是就機率方面進行討論,實際做法還是需要視當天的乘車狀況,而有相對應的方法應變之。比較討論(一)和討論(二)的內容,或許愈多出入口對人們的通勤生活會更加便利,不過,就當今的文湖線系統而言,要多建設幾個出入口通往月臺可能是困難重重的計畫,何況有些月臺還需要經過天橋才能抵達。若能透過簡單的物聯網設計,將資訊技術應用在人們的生活中,或許,以後就不必花時間去探究捷運壅擠的應對措施,也可以減少苦惱上學遲到的問題了!建議北捷可以在車廂內裝設偵測車內人數的相關儀器,再透過物聯網將前一站偵測到的各車廂人數,傳達到下一站的候車月台,例如:綠燈表示車廂內較空曠, 紅燈則反之,利用智慧生活的概念,讓乘客方便掌握車內乘客數,好判斷哪一個車廂較容易 上車。如圖所示:
教官:「如此精采的報導,教官受益良多!好吧,你今天就不處罰你了!」
小明:「耶!謝謝教官!」提醒同學們下次遲到時記得準備一篇專題報導分析你遲到的理由喔!別忘了還可以投稿數感盃喔!
- 註(一):由網路上的數據得知,文湖線的首站南港展覽館站與動物園站 2019 年 1 月份的進站 人數分別約為 32259 人次與 7740 人次,並查詢每日的總發車班次,尖峰時間和離峰時間班距會有所不同,經計算得知文湖線每日共發車約 290 班次。選擇進站人次較多的南港展覽館站 計算每班列車的平均載客量,得每班次約載客 107 人次。不過考量尖峰時間,搭乘的人次可 能會比平均值多一些,故取 128 人為估算值。(資料來源:臺北大眾捷運股份有限公司——旅運量 )
- 註(二):文湖線捷運龐巴迪列車車廂最高承載人數為93人。(資料來源:台北捷運車輛簡介 )
- 註(三):因為第一出入口與第二出入口在計算乘客選擇車門的機率時具有對稱性,故在此只說明第一出入口的機率分配。






































-200x200.jpg)







