電生磁，磁生電，就讓場論來說明吧！——《物理學的演進》

• 本文編譯自《Physicists explain how type of aurora on Mars is formed》

形成極光的要素有三，其中之一就是磁場。地球具有覆蓋全球的磁場，可以在兩極地區生成北極光和南極光；然而，火星沒有覆蓋全球的磁場，因此火星上的極光並非出現在兩極，只能在特定區域生成。

近期，愛荷華大學領導的研究團隊，根據美國航空暨太空總署（NASA）火星大氣與揮發物演化任務（MAVEN）探測器的數據，確認了火星離散極光是由太陽風和火星南半球地殼上空殘存的磁場相互作用所生成。

極光三要素：大氣、磁場、高能帶電粒子

在介紹火星前，讓我們先把鏡頭轉到地球，談談地球上的極光在哪裡形成，以及如何形成。

地球極光出現的區域稱為極光橢圓區（auroral oval），涵蓋北極與南極地區，但並非以兩極為中心；換句話說，極光橢圓區也涵蓋了極圈以外的部分高緯度地區。另外，極光橢圓區的寬度與延伸範圍，會隨著太陽黑子 11 年的循環週期而變動。

當太陽風和地球磁層的高能帶電粒子被地球磁場牽引，沿著磁力線加速往高緯度地區移動，最後和大氣中的原子碰撞時，就會形成多采多姿的極光。

綜合以上所述，可以得知極光的三個要素是：大氣、磁場、高能帶電粒子。

地球上這些「指引我們美妙未來的魔幻極光」，若屬於可見光波段，就能用肉眼觀測，並以相機記錄這夢幻舞動的光線。

極光橢圓區與地理北極、地磁北極相對位置圖。其中紅色實線表示極圈範圍，綠色區域則為極光橢圓區。圖／National Park Service

火星的大氣層、磁場以及離散極光

在介紹離散極光之前，得先介紹它的幕後推手——行星際磁場（Interplanetary Magnetic Field，IMF）。IMF就是太陽風產生的磁場，在行星際空間主導著太陽系系統內的太空天氣變化，並阻擋來自星際間的高能粒子轟擊。

那麼 IMF 是如何產生的呢？當太陽風的高能帶電粒子從太陽表面向外傳播，會同時拖曳太陽的磁力線一起離開；太陽一邊自轉一邊拋射這些粒子，讓延伸的磁力線在黃道面上形成了螺旋型態的磁場。

以蛋糕裝飾來說明的話，太陽就像是在轉盤上的蛋糕，太陽風粒子就是擠花裝飾；而當蛋糕一邊以固定速度自轉，擠花逐漸向外擴散的同時，就會在蛋糕產生螺旋狀的軌跡。

對太陽風和 IMF 有基本認識之後，讓我們把鏡頭轉向火星，談談火星的大氣層和磁層和地球有什麼不同。

相較地球來說，火星的大氣層非常稀薄。這是因為太陽風的高能粒子轟擊火星大氣層，強大的能量將大氣層的中性原子解離為離子態，導致大氣層的散失；該過程稱作濺射（sputtering），發生在火星大氣層的濺射主要透過兩種方式達成—–第一，在 IMF 的作用之下，部分的離子會環繞磁力線運動，隨著 IMF 移動而被帶離火星；另外一部份的離子則像撞球一般，撞擊其他位於火星大氣層頂端的中性原子，引發連鎖的解離反應。 

MAVEN 任務的領銜研究員 Bruce Jakosky 說明，根據團隊研究的成果，太陽風的濺射效應會將火星大氣層中的惰性氣體氬解離，並將這些氬離子從大氣層中剝離。火星大氣層內氬的同位素（質子數相同，但是質量不同的元素）以氬-38 以及氬-36 為主，後者因為質量較小而較容易發生濺射。

藉由氬- 38 和氬-36 的佔比，Jakosky 的團隊推估火星約有 65％ 的氬已經散逸至外太空。基於該研究結果還可以推算出火星大氣層中其他氣體的散逸情形；其中又以二氧化碳為焦點，畢竟行星需要足夠的溫度才能維持液態水的存在，而二氧化碳在溫室效應有很大的貢獻。

接著，讓我們一探究竟火星磁場與地球有何不同。地球能形成全球磁場的奧秘是什麼呢？這要先從行星發電機理論開始說起，該理論指出行星要維持穩定的磁場有三個要件——導電流體、驅動導電流體運動的能量來源、科氏力。

以地球為例，地核內部保留了地球形成初始的熱能，約有 4000°C 至 6000°C 的高溫。位於地核底層的高溫液態鐵，因為密度下降而上升至地核頂端，接觸到地函時，這些液體會喪失部分熱能而冷卻，因為溫度比周圍環境低，密度變高而下沉；如此不斷的熱對流循環下，讓帶有磁力的流體不斷運動，進而形成電磁感應。另外，科氏力的作用讓地球內部湧升的流體偏向，產生螺旋狀的流動效果，有如電流通過螺旋線圈移動的效果。

在火星所發現的地殼岩石證據顯示，火星在數十億年前曾經和地球一樣具有全球的磁場。科學家對火星磁場消失的原因還不是很清楚，其中一種假說認為可能跟火星質量較小有關，在火星形成之初散熱較快，造成火星外核液態鐵短時間內就凝固，無法像地球一樣，保留高溫地核使液態的鐵和鎳因為密度的變化，不斷從地核深處上升至地函，再冷卻下降，持續進行熱對流。

火星地核內部缺乏驅動導電流體的原動力，導致火星內部的發電機幾乎停止運轉，無法形成全球的磁場。話雖如此，火星仍然具備小區塊的磁場，主要分布在火星南半球留有殘存磁性的地殼上空。

磁層與大氣層相互依存，火星在太陽風不斷吹襲之下，大氣層愈趨稀薄；火星內部又缺乏發電機的動力，無法形成完整的磁層。火星缺乏厚實的大氣層保護，就難以阻擋外太空隕石的猛烈攻勢，因此如今呈現貧瘠乾燥又坑坑疤疤的外貌。

既然這樣，看似缺乏極光形成要素的火星，又是如何形成極光的呢？

雖然火星沒有覆蓋全球的磁層作為保護，但火星南半球仍帶有區域性的磁場。在那裡，磁性地殼形成的殘存磁場與太陽風交互作用，滿足了極光生成的條件。這種極光被稱為「離散極光」，與地球上常見的極光不同，有些發生在人眼看不見的波段（比如紫外線），所以也更加提升了觀測難度。

那麼，研究團隊是怎麼發現這種紫外線離散極光的呢？那就是藉由文章首段提到的 MAVEN 探測器所搭載的紫外成像光譜儀（Imaging Ultraviolet Spectrograph，IUVS）！

該團隊的成員 Zachary Girazian 是一位天文及物理學家，他解釋了太陽風如何影響火星上的極光。

火星離散極光的發現

研究團隊根據火星上離散極光的觀測結果，比較以下數據之間的關係——太陽風的動態壓力、行星際磁場（IMF）強度、時鐘角和錐角^{[註 1]} 以及火星上極光的紫外線，發現在磁場較強的地殼區域內，極光的發生率主要取決於太陽風磁場的方向；反之，區域外的極光發生率則與太陽風動壓（Solar Wind Dynamic Pressure）關聯較高，但是太陽風動壓的高低則與極光亮度幾乎無關。

N. M. Schneider 與團隊曾在 2021 年的研究發表提到，在火星南緯 30 度至 60 度之間、東經 150 度至 210 度之間的矩形範圍內，當 IMF 的時鐘角呈現負值，如果正逢火星的傍晚時刻，較容易觀測到離散極光；也就是說在火星上符合前述的環境條件很可能有利於磁重聯（Magnetic Reconnection）——意即磁場斷開重新連接後，剩餘的磁場能量就會轉化為其他形式的能量（如動能、熱能等）加以釋放，例如極光就是磁重聯效應的美麗產物。

未來研究方向：移居火星

因為火星上離散極光的生成與殘存的磁層有關，而磁層又關乎大氣的保存。所以觀測離散極光的數據資料，也能作為後續追蹤火星大氣層逸散情形的一個新指標。愛荷華大學的研究成果，主要在兩個方面有極大的進展——太陽風如何在缺乏全球磁層覆蓋的行星生成極光；以及離散極光在不同的環境條件的成因。

人類一直以來懷抱著移居外太空的夢想，火星是目前人類圓夢的最佳選擇；但是在執行火星移民計畫之前，火星不斷逸散的大氣層是首要解決的課題。缺乏覆蓋全球的大氣層保護，生物將難以在貧瘠的土壤存活。或許透過火星上極光觀測的研究成果，科學家們將發掘新的突破點；期許在不久的將來，我們能找到火星適居的鑰匙。

• 註1：IMF 的時鐘角（Clock Angle）與錐角（Cone Angle）

如何判定 IMF 的角度呢？因為磁場空間是立體的關係，我們測量 IMF 方向切線與 X、Y、Z 軸之間的夾角——也就是運用空間向量的概念，來衡量 IMF 的角度。時鐘角是指 Y、Z 軸平面上，IMF 方向與 Z 軸的夾角；而錐角則是在 X、Y 平面上，IMF 方向與 X 軸之間的夾角。

參考資料

1. Science Daily. Physicists explain how type of aurora on Mars is formed.
2. Z. Girazian, N. M. Schneider, Z. Milby, X. Fang, J. Halekas, T. Weber, S. K. Jain, J.-C. Gérard, L. Soret, J. Deighan, C. O. Lee. Discrete Aurora at Mars: Dependence on Upstream Solar Wind Conditions. Journal of Geophysical Research: Space Physics, Volume 127, Issue 4.
3. Michelle Starr. Mars Has Auroras Without a Global Magnetic Field, And We Finally Know How. ScienceAlert.
4. Michelle Starr. For The First Time, Physicists Have Confirmed The Enigmatic Waves That Cause Auroras. ScienceAlert.
5. Southwest Research Institute. SwRI Scientists Map Magnetic Reconnection In Earth’s Magnetotail.
6. 呂凌霄。太空教室學習資料庫。
7. 頭條匯。火星上的「離散極光」是如何形成的？物理學家有新發現，帶你揭秘。
8. Wilson Cheung。【北極物語】承載北極文化──極光。綠色和平。
9. 大紀元。火星上的極光是如何形成的？ 科學家解謎。
10. BBC News 中文。北極光：美國科學家首次在實驗室驗證北極光產生原理。
11. 明日科學。科學團隊藉由 NASA 的太空船所收集的資料得知火星大氣層的流失可能肇因於強烈的太陽風。
12. 台北天文館。NASA 首次繪製火星周圍電流分布圖，證實火星有磁場。科技新報。
13. 交通部中央氣象局太空天氣作業辦公室。太空天氣問答集。
14. Denise Chow. In an ultraviolet glow, auroras on Mars spotted by UAE orbiter. NBC News.
15. NASA. NASA Mission Reveals Speed of Solar Wind Stripping Martian Atmosphere.
16. NASA Goddard. NASA | Mars Atmosphere Loss: Sputtering.

火星 vs. 地球

長久以來，人類對火星充滿好奇，火星上有沒有水？那裡住著火星人嗎？這些未知，讓人類發射各種探測器和太空船前往火星，希望一探火星的奧秘！

超級巨大火山

奧林帕斯山是太陽系裡最高的火山，它比地球上最大的茂納開亞火山（MaunaKea）還巨大，如果從火山底部算起，奧林帕斯山大約是茂納開亞火山高度的兩倍半！火星的直徑大約只有地球的一半，為什麼火星上的火山卻可以長得比地球上的還高大呢？

夏威夷大島上的茂納開亞火山屬於熱點（hotspot）火山，這類火山的岩漿來自地函，熱點的岩漿從地函往上穿出地殼形成火山。因為板塊運動，地球的地殼會移動，這造成熱點穿出地殼的位置改變，時間久後，會形成一長串的火山，其中最有名的例子是夏威夷火山群島。

夏威夷群島的大島上有幾座活火山，目前大島就位在熱點上，夏威夷群島的其他火山年齡都比大島上的老，而且離大島愈遠愈老。

地球上因為板塊運動，熱點火山不會長得太大，長到一定程度，就會因為板塊運動移開熱點，沒有熱點提供岩漿，火山就會停止長高、長大。

火星跟地球不同，火星沒有板塊運動，地函的岩漿會在地殼上同一個熱點冒出，岩漿在同一熱點一直堆積長高，所以火星上的火山才會比地球上的巨大。

磁場很重要

根據科學家研究，火星早期有較厚的大氣，溫度適中，甚至表面有河川流水，跟目前的地球很類似。那為什麼火星現在會變成乾燥無水、充滿紅色沙塵的行星呢？

火星早期曾經有磁場，後來磁場消失，讓火星大氣失去防護，漸漸被太陽風剝離吹散。火星大氣壓力變小，地面上的液態水都變成大氣中的水蒸氣，大氣中的水蒸氣被太陽紫外線分解成氫和氧，流失到外太空，最後水漸漸從火星表面消失。目前火星地表的大氣壓力大約只剩地球的百分之一，而且還持續流失中！

科學家對火星磁場消失的原因還不是很清楚，有一種說法認為可能跟火星比較小有關。它的核心更小，所以散熱較快，造成外核的液態鐵凝固。外核的液態鐵凝固讓火星的磁場消失。

從火星的研究和認識，我們才明白地球原來如此特別！

真的有火星人嗎？

人類對火星上有沒有生命充滿想像，其中最有名的可能是帕西瓦爾．羅威爾（Percival Lowell）「看見」火星運河。

羅威爾是一位美國富豪，對火星非常著迷。1890 年代，他用自己建造的天文台觀看火星，並將透過望遠鏡看到的火星描繪下來。羅威爾認為他看見火星上有許多運河，建造運河是為了把南北兩極的冰運送到乾涸的赤道，這是火星有智慧生物存在的證據。

1965 年，美國的水手 4 號太空船飛掠火星，發現火星表面一片荒蕪，根本沒有羅威爾宣稱的運河和火星生命。不過，火星有生命存在的想法太吸引人，人類還是不斷用各種方式探索火星，尋找生命。

為什麼我們對火星這麼執著呢？一方面是科學上的原因，希望找到地球外的生命形態，不管這種生命形態是不是跟地球一樣，都是非常重大的發現；另一方面可能是情感上的因素，不希望地球是宇宙中唯一有生命的地方，孤單僅有的存在。

依據地球上的經驗，只要有水的地方幾乎都找得到生命，水成為生命的重要指標。火星早期比較溫暖，地表有水流動，所以火星過去可能有生命存在。科學家認為火星上最可能出現的生命是微生物，因為水存在火星表面的時間並不長，無法演化出太複雜的生命形態。

目前火星表面已經沒有穩定流動的水，不過水還是有可能存在地表下，所以，生命有可能還在火星地底存在著。人類不斷探索火星，不久的將來人類也會登上火星，到時候火星有沒有生命的問題，可能就會有答案。

• 作者｜Albert Einstein, Leopold Infeld
• 譯者｜王文生

雖然沒有任何實際參與流言散布的人真的在兩個城市間旅行，來自倫敦的小道消息，很快地傳到了愛丁堡。這個過程，涉及兩種截然不同的動作，一種和流言本身有關，從倫敦到愛丁堡；另一種，則要歸咎散播流言的人。一陣風吹過麥田，帶起一道穿過整片田地的麥浪。這一次，我們還是要分清楚波的運動，以及個別植物的運動之間的差異。植物只是稍稍晃動而已。我們曾經看過，把石頭丟進池塘中，水波的圓越來越大，藉此傳播出去。

波的運動方式，和水粒子的運動方式相當不同。水粒子只是上下運動。我們觀察到波的運動，是物質的狀態變化，物質本身並不是波。

從水面上的一顆軟木塞就能清楚地見到這個現象。軟木塞上上下下的動作，和水實際上的運動類似，它的運動不是波造成的。

為了深入了解波的機制，我們再來考慮一項思想實驗。假設在一個足夠大的空間裡，均勻地被水、空氣，或其他種「介質」填滿。空間的中央處有一個球體。實驗開始時，沒有任何運動。突然，球體開始規律地「呼吸」，體積擴張，然後縮小，在此同時維持球狀的外表。介質會發生什麼變化？我們從球體開始擴張的瞬間開始分析。緊鄰球體的粒子被推開，導致周邊一層球殼狀的水，或是空氣的密度上升，高於正常值。經由類似的過程，球體縮小時，緊鄰球體介質的密度下降了（下圖）。組成介質的粒子只是微幅振動，但是，整體的運動卻是一個行進的波。基本上，我們現在正踏入全新的領域，第一次考慮物質以外的運動，也就是經由物質傳遞的能量產生的運動。

以脈衝球體為例，我們可以導入定義波的性質時相當重要的兩項普通物理觀念。首先是速度，描述波的傳遞。它和介質有關，例如，波在水和空氣的傳播速度不同。其次是波長 (Wave Length)。在海上或河流傳遞的波，它的波長是從一個波到另一個波距離，或是一個波峰到另一個波峰的距離。因此，海上的波相較於河裡的波具有較大的波長。至於脈衝球體產生的波，波長是在某個固定時間點，兩個密度最大或最小的相鄰球殼之間的距離。很明顯，這個距離不會只和介質有關，脈衝球體縮放的速度顯然對波長有不小的影響。縮放的速度越快，波長越小；縮放速度越快，波長越大。

波的觀念在物理學取得巨大的成功。

波是力學的觀念，這點無庸置疑。波的現象被簡化為粒子的運動，而且根據動力學理論，粒子由物質組成。因此，所有用到波的觀念的理論，一般來說都能視為力學理論。比方說，聲學現象的解釋，基本上建立在波的觀念。物體的振動，像是聲帶和琴弦，是聲波的來源。聲波在空氣中的傳遞模式，和脈衝球體波相同。如此一來，將所有聲學現象透過波的觀念簡化為力學是可能的。

前面已經強調過，我們得清楚地分辨粒子的運動和波的運動，後者是介質的一種狀態。兩種運動差異不小，但是，在脈衝球體的例子，兩種運動顯然發生在同一條直線上。介質粒子在一條短線段上振盪，隨著振盪運動，介質密度週期性地增加和減少。波傳遞的方向，與振盪發生的直線的方向，兩者相同。這種類型的波，稱為縱波 (Longitudinal wave)。但是，波只有這一種形態嗎？為了接下來的討論，我們必須認知到另一種類型的波存在的可能性，稱為橫波 (Transverse wave)。

我們調整一下先前的例子。現在依然有一個球體，但是它浸在一種膠狀介質裡，不是空氣，也不是水。此外，球體不再是縮放，而是朝一個方向旋轉一個小角度，再轉回來。旋轉的節奏是固定的，轉軸也不變。膠狀介質附著在球體周遭，被迫以相同的方式運動（下圖）。一部分的力作用在稍微遠一點的地方，造成該處產生相同的運動，如此一來，介質中就產生一個波。如果我們留意到介質的運動與波的運動之間的差異，會發現它們並不是發生在同一條直線上。波沿著球體的直徑方向傳播，而介質的運動則和這個方向垂直。以此方式，我們造出一個橫波。

在水的表面傳遞的波是橫波。漂浮的軟木塞上下浮動，水波則沿著水平面傳遞。另一方面，聲波則是我們最熟悉的縱波範例。

還有一點：脈衝的球體和震動的球體，在同質的均勻介質中製造的是球形波。這是因為在任意時間點，任何圍繞著球體的球殼上的任何一點，行為都是相同的。讓我們考慮位在波源遠處，以波源為球心的球殼上的一個小塊。我們考慮的小塊越小，距離波源越遠，它就越接近一個平面。若不做太嚴謹的考慮，可以說半徑夠大的球殼上的一小部分，和平面其實沒有什麼差距。我們常常把遠離波源的球形波上的一小部分，稱為平面波。如果把下圖著色的區域再向遠離球心的方向移動，兩條半徑中間的夾角就會越來越小，更接近平面波。平面波的觀念和某些物理觀念很類似，它們是虛構的，無法以完美的精確度製造出來。然而，平面波依然是相當有用的物理觀念，不一會就能派上用場。

• 作者｜Albert Einstein, Leopold Infeld
• 譯者｜王文生

「電場的變化，伴隨磁場的產生。」如果我們把「電場」和「磁場」的位置交換，剛剛的句子變成：「磁場的變化，伴隨電場的產生。」只有實驗才能確定這個敘述是否屬實。不過，這個問題是透過場的語言組織而成。

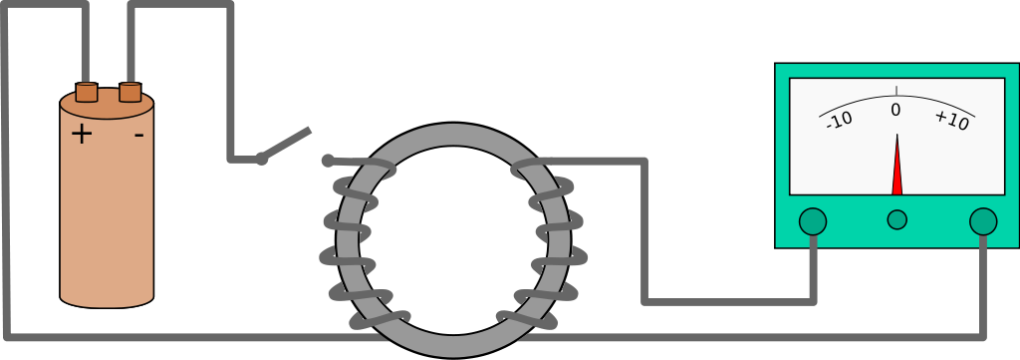
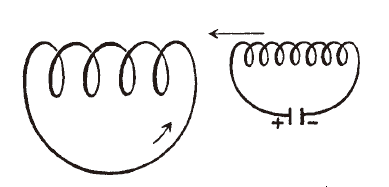
100 多年前，法拉第做了一個實驗，結果是感應電流的偉大發現。演示的過程很簡單。我們只要準備一根螺旋管，一根棒狀磁鐵，還有一個檢測電流存在的儀器，這種儀器有很多種。開始時，讓螺旋管形成一個封閉電路，再把棒狀磁鐵放在靠近螺旋管的地方，保持靜止（下圖）。導線上沒有電流，因為沒有源頭產生電流。現在只有棒狀磁鐵的磁場，不隨時間改變。現在，我們很快改變磁鐵的位置，隨喜好讓它靠近或遠離螺旋管。在這個時間點，會產生一個電流，持續時間非常短，隨即消失。當磁鐵的位置改變，電流就會出現，而且可以被足夠敏感的儀器偵測到。但是一個電流—從場論的角度看來—代表一個電場存在，迫使電流體在導線上移動。電流及電場，在磁鐵再次靜止時會消失。

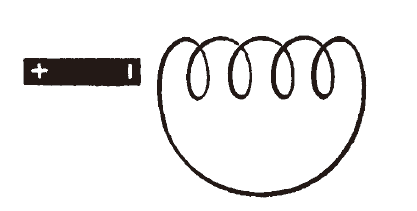
想像一下，如果場的語言還是未知，我們必須用機械論的舊有觀念，也即定性和定量地描述這個實驗結果。那麼，我們的實驗結果顯示：因為磁極的運動，創造出一個新的力，使電流體在導線上移動。下個問題是：這個力和什麼有關？這會是很難回答的問題。我們得研究力與磁鐵速度的關係，以及力與磁鐵形狀、電路形狀的關係。不僅如此，如果用舊有語言詮釋這個實驗，我們完全沒有線索能推測，如果不是棒狀磁鐵，另一個通電的電路是否能引起感應電流。

如果用場的語言，事情會變得很不一樣。我們再次相信我們的原理，也就是場可以決定作用。我們見過一次，通電的螺旋管的作用與棒狀磁鐵類似。下圖畫出兩根螺旋管，一根較小，並帶有電流；另一根較大，我們偵測到它帶有感應電流。就像我們之前移動棒狀磁鐵，我們可以移動小螺旋管，在大螺旋管上製造一個感應電流。不僅如此，即使不移動小螺旋管，我們也能透過創造和消滅電流的方式，也就是接通或斷開電路，藉此創造或消滅磁場。場論預期的新現象，再次被實驗證實！

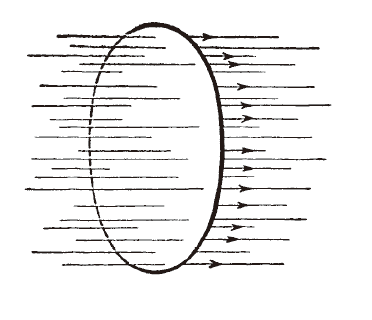
我們看一個更簡單的例子。有一條封閉的導線，上面沒有任何電流的源頭。導線的附近有一個磁場。這個磁場來自另一個通電的電路，或是某個棒狀磁鐵，對我們來說並不重要。我們的下圖，畫有封閉電路和磁場的力線。透過場的語言，感應現象的定性與定量描述會非常簡單。如同圖中所繪，有些力線穿過了導線圍繞範圍內的平面，我們必須考慮穿過該平面的力線。不論場的強度有多大，只要場沒有變化，就不會有電流。但是，只要穿越導線圍繞範圍內的平面的力線數量有所變化，環狀的導線上就開始有電流通過。電流由穿越平面的力線的數量變化所決定，不論數量變化的原因為何。力線數量的變化，是感應電流的定性與定量描述中唯一的必要觀念。「力線數量的變化」，代表力線密度的改變，我們也記得，力線密度的變化，其實就是場的強度變化。

接下來，是我們的論證鏈中必要的論點：磁場變化→感應電流→電荷移動→某個電場存在。

因此：一個變化中的磁場，伴隨著一個電場。

於是，我們發現兩個電場和磁場理論中最重要的兩根支柱。第一，是電場的變化和磁場的連結。這是從厄斯特針對磁針偏轉的實驗產生的結果，實驗的結論是：一個變化中的電場，伴隨著一個磁場。

第二根支柱連結了變化中的磁場與感應電流，是法拉第的實驗得出的結果。兩根支柱，都成為量化描述的基礎。

又一次，伴隨變化的磁場產生的電場，似乎是某種真實的東西。我們必須想像，先前電流的磁場存在於沒有測試磁極的狀況。同樣的，我們必須宣稱，在測試導線上的感應電流不存在的狀況下，電場依然存在。

事實上，我們的雙支柱架構可以簡化成只有一根支柱，也就是從厄斯特的實驗得到的結果。法拉第的實驗結果，可以從第一根支柱，加上能量守恆定律推導出來。我們之所以使用兩根支柱的架構，只是為了清楚和有效率地表達。

應該再提一下場的描述產生的另一個結果。有一個通有電流的電路，電流來自伏特電池，舉例來說，導線和電流的來源突然被分開。現在當然就沒有電流了！但是，在為時短暫的分離之中，發生了一個有趣的過程。場論再次預期到這個過程的發生。在電流斷開前，有一個環繞導線的磁場。在電流斷開的瞬間，這個磁場也消失了。因此，有一個磁場經由斷開電流而消失。穿過導線圍繞的平面的力線數量，發生了快速的變化。但是這個快速變化，不論產生的原因為何，必須創造一個感應電流。實際上更重要的是，如果磁場的變化越大，感應電流也將隨之增強。這個結果是測試場論的另一個機會。斷開電流時，必定伴隨另一個更強、暫時產生的感應電流。實驗又一次證實了這個預測。每一個嘗試斷開電流的人，一定有注意到產生的火花。這個火花展現的是快速的磁場變化所造成的巨大電位差。

同樣的過程可以用另一個角度檢視，能量的角度。磁場消失，一個火花產生。火花代表能量，因此磁場也必須如此。為了在使用場的觀念和語言時，保持物理定律的一致性，我們必須把磁場視為能量的保存地點。只有這個辦法，我們才能在描述電與磁的現象時遵守能量守恆定律。

剛開始，場只是有用的模型，後來變得越來越真實。我們透過場了解了舊現象，它也帶我們發現新的。更進一步，是能量和場的整合，場的觀念又一次被強調；同時，對機械觀來說，至關重要的物質的觀念之重要性，日漸下降。