量子電腦到底有多霸氣？終極「密碼戰」即將引爆？

本文轉載自中央研究院研之有物，泛科學為宣傳推廣執行單位

• 採訪編輯｜郭雅欣、美術編輯｜林洵安

量子電腦與密碼學

2019 年 10 月 Google 宣布實現「量子霸權」，全世界都驚呆了！量子電腦已經無所不能了嗎？其實量子霸權的意義在於：人類已經讓量子電腦做到一件古典電腦很難達成的事。不過，量子電腦的進度條的確正快速更新，未來可能帶給人類巨大的福祉，但也會顛覆現今保護我們隱私的加密系統。

中研院資訊科學研究所鐘楷閔副研究員，形容密碼學就像一場好人與壞人的戰爭，站在量子密碼學研究前緣的他，將為研之有物的讀者揭密這場沒有煙硝的資安保衛戰。

中研院資訊科學研究所鐘楷閔副研究員，專長為理論計算機科學、量子密碼學、量子複雜度理論……換成白話，就是一位在資訊科學所用理論 / 數學研究方法研究資訊科學的科學家，專攻量子計算如何影響密碼學，及其潛力與極限。
攝影│林洵安

量子電腦跟傳統電腦差在哪？

量子電腦和傳統電腦的不同，在於它利用了各種神奇的量子特性，也就是當我們以微觀的角度觀察這個世界時，那些與巨觀世界不同的特性，像是讓薛丁格的貓介於死和沒死之間的「疊加態」，或是兩個量子即使相距很遠，仍舊會依據對方狀態而決定自己當下狀態的「纏結效應」。（有關量子效應可參考「研之有物」相關文章 量子電子元件 hen 夯，但如何掌握像情人心難測的量子位元？） 當電腦擁用這些比科幻還科幻的量子特性，將克服古典電腦無法解決的難題。

不過，鐘楷閔立刻猛劃重點強調：

量子電腦不是無所不能，或是每秒鐘能做的事情比較多，它只在某些「特定（但很重要）問題」上，有比古典電腦更快的解法，只需要更少的空間和步驟。

舉例來說，未來量子電腦可能用於模擬細菌的固氮作用，將大大提升農業上製造氮肥的效率。因為細菌進行固氮作用時，有些關鍵步驟具有量子效應，模擬這些效應的複雜度將超越了古典電腦的極限。而量子電腦「剛剛好」是以量子效應運作，當然較有希望成功。

不幸的是，量子電腦可攻克的「特定問題」，也包括時刻保護我們交易安全和隱私的加密系統……

堅不可摧的加密系統

登入網購平台，輸入帳號密碼，選好商品放入購物車（又剁了好幾根手指）之後，再填好地址及電話，按下結帳，輸入信用卡卡號，接下來只要等商品來到家門口，啊～多美好的日常……等等，你算過在剛剛那五分鐘裡，親手傳出多少個人資訊嗎？這個問題細思極恐，事實上不必太擔心，因為密碼學正默默保護著我們。

早在兩千年前凱撒大帝打仗時，就懂得使用「暗號」來保護軍事書信。只有知道暗號的人可以「解讀」信件內容，對於不知道暗號的敵人來說，就算拿到書信也只是一堆亂碼。

但這套方式有個致命傷，那就是「如何一開始讓所有合法的使用者拿到一樣的暗號，又不會讓暗號外洩呢？」當代的密碼學家想出一套稱為「非對稱加密 」的方式，利用成對的公鑰和私鑰來加密暗號，公鑰就像是一個蓋上就鎖住的盒子，私鑰是可以打開這個盒子的鑰匙。如此一來，就能讓素昧平生的合法使用者，先利用比較安全的非對稱加密傳遞暗號，接下來就能靠暗號祕密通訊了。當你登入網購平台買東西，你的電腦和平台之間的通訊，就是透過類似的方式保護你的個資。

舉例來說，當顧客登入網路書店，申請刷卡購買「研之有物」的新書。網路書店會立刻製造一對公鑰和私鑰，把公鑰傳給客戶的電腦。客戶端的電腦再將自己的暗號，以公鑰加密後傳回網路書店。壞人沒有私鑰，就算中途攔截了信息也無法破解。最後，網路書店用私鑰解密，得到客戶的暗號，接下來就可以靠暗號傳送信用卡卡號等個資了。

細心的讀者可能會有疑問：那為什麼不直接把所有訊息透過非對稱加密傳遞，還需要先傳暗號，再用暗號保護訊息呢？原因在於，非對稱加密的效率非常低，而透過暗號加密（稱為對稱式加密）的效率很高。因此，目前網路架構中，僅利用非對稱加密傳遞短短的暗號，接下來主要的通訊就使用高效率的對稱式加密。
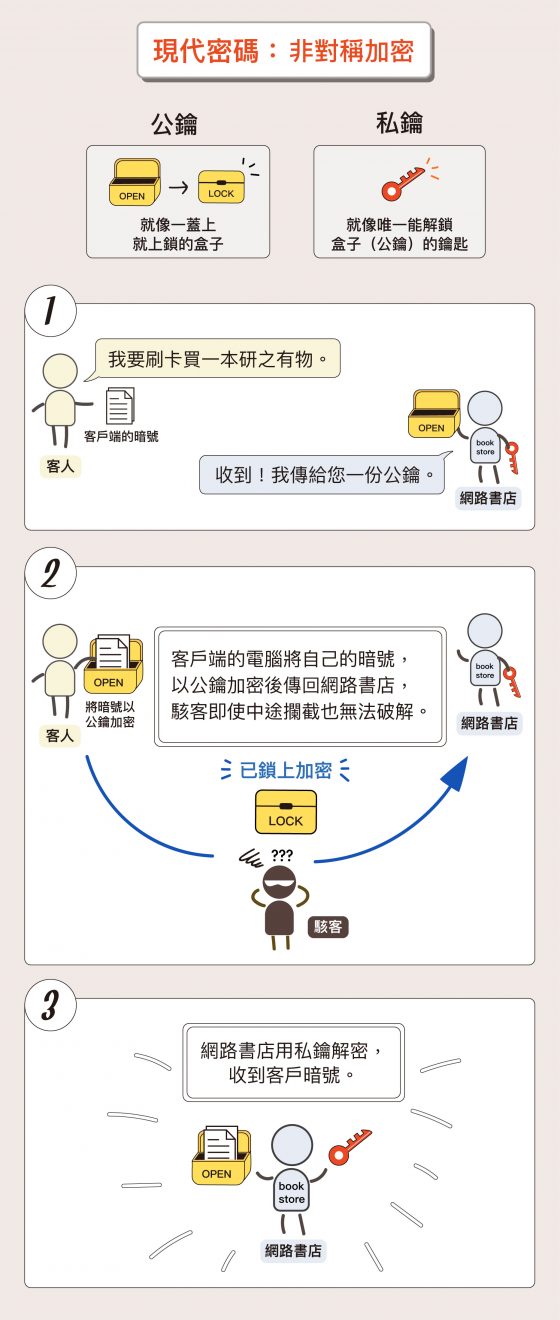
圖說設計│ 林洵安、黃曉君

當然，網路上並不是真的有一個盒子在傳輸！目前的加密系統能如此安全，關鍵是它的核心有一個難以解開的數學難題，需要公鑰加上私鑰才能解開。所以即使壞人拿到加了密的訊息，沒有私鑰還是解不了密碼。

這類數學難題很多，像是超大數字的質因數分解。隨機找兩個很大的質數相乘 ，比如 97 乘上 113 ，就會得到一個超大數字 10961 ，很簡單吧？但是，如果一開始給你 10961，你算得出它是哪兩個質數相乘嗎？

這不是國小老師偷懶沒教，而是人類還沒找到有效率的方法（多項式時間的演算法）來計算質因數分解這類問題。所以理論上，只要數字夠大，即使是全世界性能最強大的超級電腦，也可能花費上萬年才能破解。

簡言之，加密系統核心的數學難題愈困難，古典電腦就需要花愈長的時間破解，加密系統也就愈安全。

破解古典密碼，量子電腦 hen 會

然而，現今密碼學看似堅不可破的數學難題，在量子電腦的面前變得不堪一擊。因為這些問題的答案都可以轉化成週期性的結構，剛好量子電腦擅長破解。（哭哭）

什麼是週期性結構？再以質因數分解問題舉例：想要找出 N 這個數字是由哪兩個質數 (P 與 Q) 相乘所得，可以先任意選擇一個數字 A ，用 A 去除 N ，得到一個餘數 a1 ，接下來依序用 A2 、 A3 、 A4 ……不斷地除 N ，就會得到餘數 a1 、 a2 、 a3 、 a4 ……最後某一次的操作，餘數會回到 a1 ，形成週期性的結構。一旦能找到週期，就能「比較有效率」的分解 N。

不過，對於古典電腦來說，當數字相當巨大時，尋找餘數的週期仍是十分困難的任務，但對於具有疊加作用的量子電腦，卻是小事一樁。

總之，目前我們所仰賴的加密系統，在量子電腦出現之後將變得不再安全……可是 IBM 、 Google 不斷更新量子電腦發展的進度條，我們已經暴露在資訊外洩的風險之下了嗎？

別擔心！小亞瑟還沒長成惡魔小丑

其實，量子電腦目前還只是個嬰孩階段。以 Google 用來實現量子霸權的量子電腦來說，只有 53 個位元。

相較古典電腦，早在 1970 年即已發布 Intel 1103 ，為容量 1 kb (1024 位元) 的記憶體。「古典電腦如果只有 53 個位元的記憶體，連程式都沒辦法寫，英文字母只能存 7 個，可以想像現在的量子電腦 Size 有多迷你。」鐘楷閔笑著繼續解釋：「而且如果把 Google 做的事情畫成一個量子電路，這台電腦能執行的電路深度最多只有 20 層。」翻譯成大白話，意思是：每個位元只能運算 20 次！

「20 次？！這麼少？」你發現重點了！量子位元操作時很容易受到環境影響而壞掉， 20 次的操作已是目前的極限。

Google 公布的 53 個位元量子電腦。上圖每個灰色 X 皆是一個量子位元，白色的 X 是壞掉的量子位元，下圖為幾公分大的量子電腦晶片，量子位元統統擠在這小小的晶片中。
圖片來源│《Nature》

不只如此， Google 這次霸氣外漏的宣告，他們讓量子電腦做的事情，其實是……模擬量子電腦自己！「哈哈，這題目有點作弊嫌疑啦！不過，這依然是一個很重要的結果，證明了即使現在量子電腦這麼小，已經可以做到一件古典電腦做不到的事了。」鐘楷閔笑著解釋。

這個任務有多難？如果古典電腦試圖模擬同樣的量子系統，必須先將量子態用 0 與 1 記錄下來，再計算這些 0 與 1 經過 20 次量子運算會有什麼改變，最後才能得到結果。可是古典電腦光是要把這 53 個量子位元的狀態寫下來，就需要 2⁵³ 個位元的空間，更別提運算和模擬了！ 根據 Google 論文宣稱，古典電腦要完成這件事得花一萬年，但這臺小小的量子電腦只需花 200 秒。

Google 實驗的意義在於：我們已經可以控制 53 個量子位元完成 20 次的操作，這是一件目前古典電腦做不到的事。

但是，這距離真正「有用」的量子電腦還有很遠的路！拿量子電腦模擬細菌固氮效應來說，量子電腦得擁有 100 個左右的量子位元，並且可以運算操作 10¹⁴ 次……。 想想，Google 的量子電腦只有 53 個位元不說，而且只能操作 20 次，簡直天壤之別！至於量子電腦破解現在的加密系統，根據專家預測，嗯……至少還要 30 年的時間。

終極密碼戰，現在就開打！

雖然如此，但密碼學已深入現代生活的層層面面，不早點找出應對之策，屆時可就來不及了。想想全世界在千禧年危機的手忙腳亂、損失慘重……

從 2017 年起，美國國家標準暨技術研究院 (NIST) 開始著手「後量子密碼標準化計畫」，募集全世界密碼學家研發、可對抗量子電腦的密碼系統。這些密碼系統的核心同樣有個數學難題，但這個難題無法轉化成量子電腦擅長的週期性問題，中研院資訊所楊柏因研究員團隊也參與這個計畫，並通過第二輪選拔。

「整個過程就像選秀節目一樣，」鍾楷閔笑著形容：「主辦單位先海選出合適的密碼系統，然後經過兩輪篩選，訂定標準化的各項參數，預計在 2022 ~ 2024 年間公布最終標準。」

簡言之，在 3-5 年後，我們很可能就會開始逐步更新密碼系統，正式進入「後量子時代」。

這場密碼學的競賽，就像好人與壞人的戰爭。究竟是壞人會先利用量子電腦破解加密系統，擊潰目前的資訊安全網，還是好人會先做出安全的後量子時代加密系統，築起更安全的防禦牆，關鍵就在這幾十年量子電腦的發展。

科技進步不會停止，在量子電腦發展過程中，密碼學家正努力追趕進度，為人類預先設下資訊安全網。下次在網路上輸入個人資料時，不妨感謝一下在螢幕後頭默默努力著的密碼學家們（合十）。

原來量子電腦還在嬰兒階段，只能運算 20 次啊……想要它的運算次數快速成長，有沒有什麼好辦法？

其實，不太可能期待一個量子態經過多次的運算操作還不會壞掉，所以我們應該換一個概念：當做了一定的計算，量子態開始有一點點壞掉時，立刻修復它。換句話說，如果能成功幫量子位元隨時除錯，那它的計算次數就可以無限多。

為此，科學家正在研發如何替量子位元編碼，變成「邏輯量子位元」。所以有人認為，量子電腦的下一個目標，應該是先實現邏輯量子位元。

另一種有趣的想法是，如果把操作有限的小型量子電腦，配上古典電腦，也許可以相當於大型量子電腦……

小型量子電腦 + 古典電腦 = 大型量子電腦，這個點子感覺有戲！

可惜的是，沒有這麼便宜的事！我的團隊最新的研究，在某個模型下，反駁了英國密碼學家喬茲薩 (Richard Jozsa) 提出的類似想法「喬茲薩猜想」。

喬茲薩猜想的意思是：所有可以被大型量子電腦解決的問題，運算步驟都可被拆解，然後由小型量子電腦（只能進行少數次數操作）搭配上古典電腦解決。如果這樣的猜想為真，意味著不需要強大的量子電腦（能夠進行很多次操作），只要小型量子電腦和古典電腦合作，也能解決所有大型量子電腦可以做的事。

資料提供│鐘楷閔
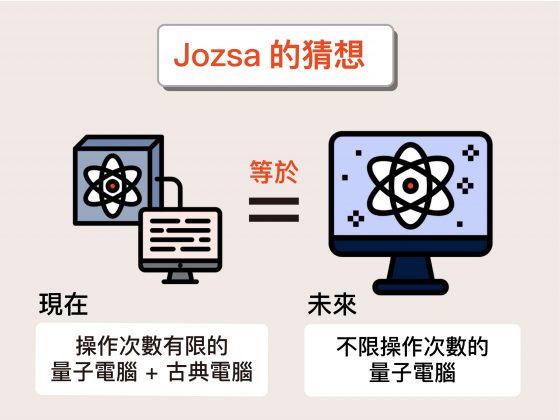
圖片重製│林洵安

我的團隊則在密碼學的一個「預言機模型」 (oracle model) 下提出一個問題，證明量子操作次數不夠多的時候，這個問題無法解開，為這個猜想找到了一個反例。

真可惜……除了量子電腦本身，鐘老師對於量子密碼學還在進行什麼研究呢？

我另一項研究重點，與密碼學的安全性證明有關。前面說過，密碼系統的核心是一個數學難題，換句話說，一個密碼系統的安全性必須仰賴這個數學難題是無法被破解。

我們可以用數學來證明這些密碼系統的構造有多安全，但對應的量子版本我們還在研究中。

因為愈好的證明，愈能確保加密系統的安全性。尤其在 NIST 正如火如荼找出後量子時代加密系統的現在，我們能做到多好的證明，也會影響標準化的參數要怎麼設定，才能滿足運算速度夠快，但又非常安全的需求。這是現代密碼學家非常重要的任務。

延伸閱讀

• 鐘楷閔個人網頁
• 量子電子元件 hen 夯，但如何掌握像情人心難測的量子位元？
• 〈奇妙的量子棋步〉，《科學人》第 11 期。
• 〈量子金鑰鎖住鈔票〉，《科學人》第 170 期。
• 〈量子電腦是什麼？〉，國家實驗研究院網頁

本文轉載自中央研究院研之有物，原文為量子電腦到底有多霸氣？即將引爆終極密碼戰？！，泛科學為宣傳推廣執行單位