「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:陳宥諼、林昱佑/國立科學工業園區實驗高級中學

最近在網路上看到了一則去年的新聞:一名在學術期刊等公共平台發表了高達 200 多篇論文的日本麻醉醫師──藤井善隆,被抓到長期偽造數據,並有高達 183 篇論文遭到撤稿,且數量仍持續增加。引起學界注意的投訴信中說道:「藤井的研究數據完美到難以置信。」
最早開始懷疑藤井數據造假的人之一,英國麻醉師 John Carlisle 觀察了藤井一百多批藥物實驗的數據,並計算了那些數據的隨機分佈,結果發現藤井的數據在統計分析下其實「發生機率極低」。也就是說,藤井的數據雖然看起來漂亮,但實際上卻是「不自然的」。
這使我們產生了興趣:我們所認定「正常」、「隨機」的數據,會不會只是我們主觀直覺思考時所產生的假象?然而事實上卻不符合真實機率?讓我們看一個簡單的例子:
假設老師出了一項作業,請學生每人投擲一枚公正硬幣1000次,並記下每一次的結果;但是,這項作業實在是太繁瑣了,學生們都想直接自己編數據交差了事──「反正,本來得到的結果就是『隨機』的啊!我只要在記錄表上隨便填上「正」或「反」就好了!」於是,大部分的人會編出類似這樣的數據「正反反正反正正反正反反反正……」看起來真的「很隨機」呢!
可是,收作業當天,老師卻一眼就找出了所有偷懶的同學(絕對不是因為有內鬼!)──「你們還太嫩了!實際去丟銅板要丟出這種結果,機率還真的不是一般的低啊……」老師一臉不屑的說。
「機率」?!終於有同學抓到關鍵字了。
其實,如果真的自己丟銅板的話,會發現可能出現這樣的結果:「……正反正正正正正正正正正正反正正正正……」怎麼連續這麼多的「正」啊!不過,如果反過來想,要是丟很多很多次,卻沒出現連續好幾個相同面朝上才奇怪呢!
什麼意思呢?以機率的角度來看──
假設丟一個公正銅板 n 次,求至少出現 1 組連續 y 個以上正面朝上的機率。
則機率 f(n)=(令擲出結果正面朝上為「+」、背面朝上為「-」;連續y個以上「+」為串列S)
1.若 0<=n<y
因為擲的次數不滿 y 次,所以就算全部擲出正面,也無法滿足條件。故,f(n) = 0
2.若 n=y
必須保證每一次都擲出正面,而每一次擲出正面的機率都是 1/2 ,所以:
f(n) = (1/2)^y
3.若 y<n<(2y+1)
最多只可能出現1組S,且要擲出S只有兩種方法:
(1) 在前 n-1 次就已經擲出 S (令機率=g(n)):如果前 n-1 次已經擲出 S,不管最後一次(第n次)擲出「+」或「-」,都不會影響結果。故
g(n) = f(n-1)
(2) 前 n-1 項未出現 S,擲出最後一項為「+」,和前面的「+」合併後恰形成一個S (令機率=h(n))
此即保證最後的至少 y 項皆擲出「+」(即 (i)第n-y+1項到第n項一定為「+」)。然而,若 S 的長度 >y (即第n-y, n-y-1, …項也為正),那麼在前 n-1 項時,就已經形成 S 了,機率就又回到 g(n)。所以,可以保證 (ii)此種方式的第n-y項絕對不為「+」。
另外,還須確保前n-y-1項未出現S:由於n< (2y+1),已經確定第n-y項為「-」的情況下,第1項到第n-y-1項最多只有2y(全部)-y(最後湊出的S)-1(為「-」的第n-y項)= (y-1) 項,就算全部擲出「+」也無法湊出 S (即 (iii)欲使該區間內未出現S的機率為100%)。
考慮(i)、(ii)與(iii),可求出機率為:
h(n) = (1/2)^(y+1)*100%
由 (1) 和 (2) 兩種方法可得出,y< n< (2y+1)時:
f(n) = g(n)+h(n) = f(n-1)+(1/2)^(y+1)
4.若 n>= (2y+1)
想要達成條件同樣有 2 種方法,且要注意可能出現 2 組以上的 S:
(1) 在前 n-1 項就已經出現 S (令機率為g(n))
同3.(1):如果在前n-1項就已經符合條件(即至少有一個S),那麼不管最後一項擲出「+」或「-」都不影響,故得:
g(n) = f(n-1)
(2) 前n-1項未出現S,擲出最後一項為「+」,和前面的「+」合併後恰形成一個S (令機率=h(n))
加上最後一次(第n次)的「+」恰形成一個S,即第 (n-y+1)項到第n項都必須保證為「+」,且第n-y項為「-」, (i)此機率為(1/2)^(y+1)。同時,還要考慮第1項到第n-y-1項中不能出現S:由於n>= (2y+1),該區間是有可能存在另一個S的,因此要避免其的機率為 (ii) 1-f(n-y-1)。
綜合與(i)與(ii),得出:
h(n) = [1-f(n-y-1)] / [2^(y+1)]
故,若n>=(2y+1),則機率等於:
f(n) = g(n)+h(n) = f(n-1)+ [1-f(n-y-1)] / [2^(y+1)]
所以,由上述討論,可推出其遞迴關係式為:
回到銅板問題:若取 y=10,以程式執行計算後——當擲銅板次數 n=1421 時,
f(1421)=7, 255, 778, 711, 927, 407, 617, 380, 544, 769, 173, 867, 806, 169, 361, 486, 522, 866, 802, 980, 651, 539, 660, 838, 223, 377, 066, 752, 145, 420, 755, 231, 929, 187, 093, 761, 722, 303, 645, 267, 912, 580, 455, 689, 572, 071, 800, 452, 693, 464, 700, 240, 325, 620, 941, 411, 943, 308, 843, 940, 722, 468, 017, 918, 536, 598, 081, 098, 266, 744, 747, 888, 440, 887, 321, 884, 634, 359, 498, 815, 523, 739, 396, 906, 549, 246, 415, 109, 283, 793, 846, 209, 720, 465, 402, 081, 202, 745, 609, 492, 452, 509, 025, 795, 069, 716, 361, 505, 310, 397, 746, 161, 836, 302, 227, 941, 580, 885, 870, 210, 044, 773, 666, 072, 022, 038, 700, 421, 605, 273, 419, 973, 038, 879, 144, 857, 154, 157, 912, 879, 478, 392, 261 / 14, 5 06, 540, 244, 799, 649, 295, 363, 967, 385, 272, 259, 250, 661, 462, 164, 996, 145, 242, 670, 971, 396, 368, 427, 928, 550, 752, 333, 318, 302, 269, 391, 954, 931, 996, 110, 373, 344, 247, 437, 783, 405, 976, 812, 508, 208, 014, 387, 645, 084, 573, 461, 084, 331, 611, 962, 071, 030, 245, 089, 177, 219, 397, 347, 545, 783, 897, 084, 779, 561, 785, 928, 834, 057, 620, 352, 012, 602, 971, 900, 896, 382, 103, 058, 767, 619, 551, 583, 898, 875, 428, 087, 721, 830, 150, 897, 600, 890, 899, 165, 970, 697, 060, 836, 381, 274, 022, 825, 694, 219, 432, 474, 834, 063, 680, 015, 967, 772, 773, 093, 077, 100, 779, 252, 371, 658, 190, 278, 159, 625, 450, 473, 401, 620, 223, 010, 779, 161, 044, 426, 883, 596, 288
(這是一個分數,並且是精確數字,由此可見計算的繁雜度!)
總之,f(1421)≒0.5001729281748267≒50%。也就是說,當擲 1421 次銅板時,出現至少一組連續 10 個以上正面的機率就已經略超過 1/2。另外,當擲 3288 次時,機率會再近一步提升至 80%;甚至擲 9391 次,機率已經達到 99%。換句話說,假設擲 1 萬次,幾乎可以保證一定會看到至少一組連續 10 個以上的正面。
然而,一般人在編造數據時,很少會連續寫下很多個正面(或反面),因為直覺上要連續擲出那麼多次相同的結果機率應該很低。正是利用這點,所以,光憑「是否出現連續多次相同結果」這個事件,就足以初步判斷數據的真實性,更遑論除此之外,還有更多事件的真實發生機率也有待計算。想要得出符合真實機率的「完美」數據,與其絞盡腦汁、分析各種事件的機率(而且不太可能分析的完),倒不如穩扎穩打的完成,或許還快些。
再者,在學校偽造作業數據頂多受到老師的批評或輕微的懲罰;但出社會後,要面對的可能是正式的論文、一份財報、甚至是一份關乎人命的實驗報告!造假的後果除了損失聲譽、失去工作,更有可能因此遭受牢獄之災。與其耗費大量精力試圖求出「毫無破綻」的造假方法,卻還要冒著被拆穿的風險苟且偷生,還不如腳踏實地,安分地完成任務,才是正道!


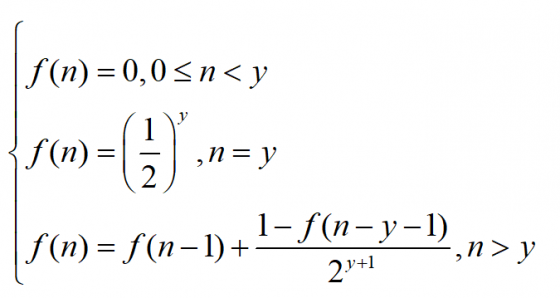
































-200x200.jpg)








