人生大事難以抉擇？用「最佳停止點」來幫助你下決定吧！

本文由 高柏科技 合作，泛科學撰文

林唯耕剛回台灣任教時，曾在清華大學的實驗室裡用一立方公分的「氨」做實驗。沒想到氨氣意外洩漏，那股刺鼻的氣味瞬間瀰漫整棟大樓，引來眾多師生抗議。

「從此以後，我再也不敢在實驗室裡用氨了。」他在《思想實驗室》的訪談中，帶著笑意回憶這段往事。

這段插曲聽來像是一則工程師的寓言：在理論模型中，氨是太空熱控系統的理想介質；但在現實的辦公大樓裡，它首先是逼人逃竄的臭味。公式本身沒有錯，但現實世界永遠比公式更複雜——它包含了人、成本、風險，以及必須為後果負責的工程師。

高柏科技技術專家、清華大學榮譽退休教授林唯耕 ，曾任職於美國 OAO 工程部熱流組，深耕電子構裝散熱與熱管技術多年。隨著 AI 浪潮席捲全球，他鑽研一輩子的老問題再次被推向科技產業的核心：當晶片運算速度無止境攀升，那股伴隨而生的熱，究竟該往哪裡去？

熱不會讀新品發表會

科技巨頭在發表會上熱衷於談論大型語言模型、GPU 規格與驚人的算力。這些詞彙在投影片上光鮮亮麗，彷彿進步毫無邊界。然而，每一次數位運算都紮實地發生在實體晶片上。晶片會發熱、材料會疲勞老化，一旦設備過熱，系統便會降頻保護。在物理現實面前，再動聽的發表會敘事也必須低頭。

回顧個人電腦發展早期，晶片幾乎不需專屬散熱元件。隨後，鋁製鰭片、風扇、熱管到均溫板逐一登場。這段歷程常被視為技術升級，其實更像是對空間的極限勒索：晶片功率翻倍，發熱源的面積卻沒變大，機箱空間也不可能無限擴張。

林唯耕指出，散熱設計的核心只有三要素：功率、熱源面積與空間限制。他舉例，在標準的 1U 機箱中，若發熱面積約為三十乘三十毫米，氣冷系統在達到八百瓦時就會面臨瓶頸。這並非固定的物理常數，而是取決於空間、面積與氣流的動態平衡。最現實的代價在於，風扇轉速提升的背後，是噪音、電力損耗與空間占用。

因此，「液冷技術」的興起並非單純為了追求酷炫，而是算力密度提升後的必然選擇。它能更精準地帶走晶片廢熱，卻也將新的挑戰帶入機房：漏液風險、流道堵塞、材料相容性，以及維運時的難度。工程的進步，本質上鮮少是徹底消滅問題，更多時候是選擇一組「比較值得承擔」的新問題。

太空教他的，不是把答案搬回地面

太空熱控工程之所以迷人，是因為它剝奪了地球上最常見的散熱工具。在真空宇宙中，沒有空氣能讓風扇製造對流；受光面溫度破百度，陰影處卻極度嚴寒。工程師必須純粹仰賴熱傳導、熱輻射，以及熱管與環路型熱管（LHP）來搬移熱能。

熱管運作的關鍵在於「相變」——液體蒸發時吸收大量潛熱，冷凝後重回循環。林唯耕比較了銅與水的熱傳導能力：在他設定的特定條件下，實心銅塊約能傳導 120 瓦的熱能；但若每秒有一立方公分的水發生蒸發相變，移熱量可瞬間拉升至 2.4 千瓦（kW）。他強調「每秒」的觀念，因為散熱談的是動態流動速率，而非靜態的冷卻魔法。

儘管如此，太空科技並不能直接套用到地面。太空元件因考量重量、功耗與維修難度，偏好無馬達幫浦的被動式設計；但地面 AI 伺服器面臨更高的熱負載與環境溫度，往往仍需幫浦驅動流量。當年那場「氨氣洩漏」事故正是最好的提醒：技術是否「先進」，與它是否「適合」當下的場景，始終是兩回事。

好論文，為什麼仍可能造不出好產品

學術研究致力於證明「可行性」，而工業現場則要求「可重複性」——不僅要能運作，還得確保每台出廠的設備都不漏水。林唯耕將此定義為「從 0 到 1」與「從 1 到 100」的差別。後者涉及良率、成本、公差與客戶信任。論文中那次最完美的實驗數據，在產線上往往未必管用。

他從不避談失敗。在高柏科技早期與學界合作時，也曾遇過實驗數據無法複製，或研究方向偏離產業需求。這未必是雙方努力不夠，而是彼此對「成功」的標準不同。為了解決這道鴻溝，高柏科技推動「柏苗啟航創新培育計畫」，每年投入逾千萬資金與成大、中山、台科大等校合作，並指派專業人才在過程中持續微調、校正，確保研發貼近產線現實。

他分享了近期一項液冷工質校正專案。團隊使用非侵入式的超音波流量計進行觀測，但由於儀器預設以「水」校正，換成其他化學流體後讀數便出現誤差。最初嘗試用幫浦壓差推算，卻發現缺乏重複性，數據甚至推導出不合理的蒸發率。最後團隊回歸基本面，改用秤重法搭配能量平衡進行交叉驗證，才讓數據成功收斂。

這個故事真正的價值不在於「產學雙贏」的口號，而在於那段不夠優雅的挫折：假設失效、數據混亂、方法砍掉重練。也正是在這種時刻，企業需要的不只是會算數的人才，而是能洞察研究何時「走鐘」，並有權力喊停、要求重來的關鍵決策者。

林唯耕坦言，過去在校園裡總認為「技術第一、成本第二」，進入商界後才驚覺行銷與信任關係往往才是關鍵。這番話雖然不如科技突破那樣動聽，卻是產品能否進入市場的殘酷真相。再卓越的散熱設計，若無法穩定生產或贏得客戶信任，也僅止於一份精美的報告。

AI 會給答案，誰來負責出貨？

訪談尾聲，主持人國威提出了一個時代難題：假設 AI 能在彈指間生成散熱架構、材料配方與流道設計，企業該選擇全面擁抱 AI 的速度，還是保留緩慢但穩定的工程驗證，以規避潛在的失效風險？

林唯耕拒絕落入二選一的框架。他的觀點是：兩者並存。AI 擅長處理資訊、生成草案；但工程師仍須實作原型，進行嚴苛的性能與可靠度測試，最終由人決定是否出貨。這並非盲目崇拜人類直覺，而是基於一項事實：AI 的資料庫裡，通常沒記載下一次「意外洩漏」或「材料疲勞」的細節，且模型永遠無法為量產結果擔負法律與商業責任。

在 AI 時代，最稀缺的未必是熟練下指令（Prompt）的人，而是具備這種能力的人：能預判答案可能在哪裡出錯、能設計實驗將問題「逼」出來，並且願意為最終的量產品質負起責任。

大眾習慣將雲端想像成輕盈、無重量的空間。但現實中，雲端是由龐大的機房架構而成，裡面裝滿了晶片、管線、泵浦與冷卻液。虛擬算力的每一次擴張，都會在實體世界留下發熱的足跡。散熱工程師的價值，就是不讓這筆物理帳單，被埋沒在光鮮亮麗的投影片背後。

隨著年齡增長，我認知到兩件事實：第一、味全龍不會復活；第二、戀愛是場妥協的過程。

高二那年，我第一次去光華商場

「我要組一台完美的電腦。」

「完美是怎樣，記憶體、螢幕、CPU要衝多快、主機板、音效卡、顯示卡、鍵盤、滑鼠？」

「滑鼠跟鍵盤那種事情不重要啦！」

我心虛地反駁老闆，根本沒想過原來「完美」是由眾多細節構成。

完美的情人也是如此吧。每個人想找到完美情人，但具體地說又是怎樣呢？

我思索了好久，深夜夢到完美情人，醒來便記下她的樣貌、感覺，我彷彿在寫生，景物是藏在腦海深處的她：清澈的雙眼，我可以在她瞳孔中看見自己的幸福表情；挺拔的鼻子，親吻時我們的鼻尖會微微碰到；總是帶著淺淺的笑，不刻意，像中餐吃了頓好的，或順利完成工作，對生活滿足的笑容；孝順善良，為了小事感傷，面臨抉擇時有主見。

還有他的身高應該要是 158 公分，據說 12 公分是最佳的擁抱差距。最重要的是，她會像我愛她一樣地愛著我。

關於完美情人，你得像組裝電腦一樣列出所有細節，再將它們統整成一個多重最佳化（multi-objective optimization）問題。列出來就好了，幹嘛變成最佳化問題？

因為世界上不存在完美情人。柏拉圖曾說過，這世界上沒有完美的直線。再精確的尺也只能畫出近似的直線，無限放大後必然會看到抖動。

任何感官能體會到的事物都是表象，是完美的理型（form）的投影。直線的理型，存在於抽象的數學世界中。情人的理型，只存在於每個人的腦海裡。現實中我們尋求的，是最接近理型的情人。

我們想最佳化數個目標函數，或是說，想找到一位情人能在各方面都最接近理型。如果有這麼一位對象，恭喜你。但現實中常常事與願違，你可能找到一位外表很相似，但現在同時有兩位男友而你只能排到星期六下午三點到五點，跟吃到飽下午茶的時段差不多；你可能找到一位很聊得來的女孩，但懊惱自己為何都三十歲了還在意外表。你可以找到許多帕累托最佳解（Pareto Optimality）。但真正的理想情人只有一位，越多「一樣好」的帕累托最佳解，只更證明了他們距離理型更遠。

你終究要從眾多的「帕累托情人」當中挑出一位，我們進一步將多重最佳化改成階層最佳化（hierarchal optimization），把目標分等級，依序追求，先是個性、再來是外表、再來是喜不喜歡狗……很多人交往或結婚後感情生變，我認為很大一部分就是階層最佳化的順序改變了。交往前最在意的是長相，但交往後相處卻認為個性最重要，原本喜歡的對象就變得不再那麼美好。

這是妥協的下場，奈何我們只能跟這個下場妥協。

※

讓我繼續來潑冷水。當我們從理型退到帕累托最佳解，再用階層最佳化求得一位對象，且稱她為「最佳解情人」。

問題是，你不一定能遇到她。更糟糕的是，遇到了也不一定知道是她。

哪怕你覺得眼前的對象已經很不錯了，但她終究跟理型有一段差距，這差距會讓你心底永遠存留一個小小的疑問。

娶了紅玫瑰，久而久之，紅的變了牆上的一抹蚊子血，白的還是『床前明月光』；娶了白玫瑰，白的便是衣服上沾的一粒飯黏子，紅的卻是心口上一顆硃砂痣。——〈紅玫瑰與白玫瑰〉

是否存在一位更好、更接近理型的情人？

秘書問題（secretary problem）試圖解決這個問題：假設一輩子交往 100 位女朋友，而且分手了就不能復合，那麼前 37 位都不能定下來，只能將他們作為你的參考指標。第 38 位起，倘若有一位比前 37 位都要好的對象出現，立刻下跪求婚，如此將可最大化你和最佳解情人定下來的機率。

這是一套經過數學嚴謹計算的最佳策略，使用起來的成效是—— 1/e，e 是歐拉數（Euler’s number），趨近 2.718，換算起來 1/e 是 37%。表示你有高達六成的機率會錯過她。

夠沮喪了嗎？讓我再推你一把。

方才的 37% 是指你跟最佳解情人交往過的前提下才成立，換句話說這是條件機率。有更多的可能是根本沒和最佳解情人交往過，甚至連認識都不認識她。

撇開你我都不是金城武的事實，倘若認識了最佳解情人就能順利和她交往，則和最佳解情人定下來的機率是

P（和最佳解情人定下來）= P（和最佳解情人定下來|認識最佳解情人）× P（認識最佳解情人）+ P（和最佳解情人定下來|不認識F）× P（不認識最佳解情人）= 37% × P（認識最佳解情人）+ 0 × P（不認識最佳解情人）

認識最佳解情人的機率有多高呢？

我們用費米推論法（Fermi estimation）來算算看。假設最佳解情人住在台灣，台灣 20~40 歲女性約三百五十萬人。在假設社交網路中，你只會認識朋友的朋友，也就是圖論中的距離（node distance）2，倘若你有 200 位朋友，每一位認識 200 位這個年齡層的台灣女性。用這麼寬的標準來算，依然只有 1% 的機率，你會認識最佳解情人。這時候，和最佳解情人定下來的機率將銳減到 0.37%。

到這邊，我相信你對愛情已經不再抱著過度的期望，畢竟數學告訴我們，儘管每個人都花了一生的力氣在尋找真愛，但這麼說好了，把你的人生想成是一張剛買了咖啡後拿回來的發票。

你覺得手中的發票會中獎嗎？

不好意思，我中了，而且是頭獎。

※

那是一個普通的傍晚，從奇岩站搭 33 分鐘的捷運到台北 101，搭電梯上 57 樓會場，擔任朋友舉辦的講座主持人。開場前我走進會場，她獨自坐在右側，臉上掛著淺淺的微笑，不刻意，讓人覺得可能是中餐吃了頓好的，或順利完成工作，對生活滿足的笑容。

我經過她凝視的前方，竊取了她的笑容。她對這奇蹟的一刻彷彿渾然無所覺，她不知道，我的情人理型以最不失真的角度立體投影在這個空間內，以白襯衫，搭配粉紅色針織罩衫的樣貌出現。

1 個月，我們第一次約會；2 個月，我們交往；3 個月，我向她求了一場很爛的婚；5 個月，我補了一場比較好的求婚，我們在日本訂做婚戒；8 個月，我們登記為夫妻，在外頭租了間小公寓，房東在牆上貼了一片櫻花送我們，我們天天在櫻花樹下睡覺，做著粉紅色的夢；13 個月，我們搬回北投住；21 個月，我們舉辦這場婚禮。每段時間，我們都有值得珍惜的重要回憶。1, 1, 2, 3, 5, 8, 13, 21……稱為費波納契數列，第 n 個數字是前兩個數字相加的結果，費波納契數列連續兩個數字相除，1/1=1, 1/2=0.5, 2/3=0.67, 3/5=0.6, 5/8=0.625……會越來越接近黃金比例：0.618，在數學中被視為美的同義詞。

※

交往中，我察覺到自己犯了根本上的錯誤。

我總以為愛情是追逐一位最接近理型的情人的過程。她相當接近，也僅止於接近，始終不是百分之百。但儘管如此，我們的相處依然那麼契合，如同以黃金比例做成的潘洛斯鋪磚（Penrose Tiling），只需要兩種基本形狀：飛鏢（Dart）與風箏（Kite），便能完美鋪滿整個平面，不留下一絲縫隙。

後來我才知道自己弄顛倒了。

的確，現實生活中不可能有一條完全筆直的直線，它只存在於想像中；但情人跟一條直線不一樣，情人是主觀的，是有很多細節想像不到，唯有相處、經歷後才清楚。因此，想像中不可能有完美的情人，情人的理型就是茫茫人海中的某位女孩，腦海裡的想像只是投影，讓我們用來按圖索驥，去尋找理型，那一位對每個人來說都是獨一無二的另一半。

我中的不是頭獎，是任何一個單位都無法兌換給我的超級特獎，是屬於我的情人理型。

本文原刊登於作者臉書網誌〈情人的理型〉，經作者授權轉載。

「打從一開始，R101計畫就是靠意識形態而非常識來推動。R101號必須不計一切代價，趕在1930年10月的某個日子飛航印度，因為湯普森大人(當時英國工黨上院議員，曾任航空部長，『飛船』開發強力推行者)將在那天搭乘R101號，進行由倫敦往返喀拉蚩的處女航，並在航程結束後，及時趕回倫敦參加帝國會議…它終於在惡劣的天候中起飛，全身溼透，飛行八小時後，終於在法國北方一處曠野中墜毀燃燒。飛船上共載有五十四人，只有六人生還。…因為這樣一樁慘案後(即便同期有另一艘大致成功的R100案例)，再也沒有乘客自願進行另一趟飛船飛行。大英帝國的飛船紀元也正式畫上句點。」

這是「想像的未來」一書描述，一段消失的巨型飛行器—「飛船」的故事，相較於現今現實滿天「重於空氣」的飛機，這種曾一度轟動登場的「輕於空氣」的飛行科技可以算是悄然走入歷史，走入幻想創作，人類文明及其與天空之間的共同命運也走上了一段不同的樣貌！

今年閱讀「科技恩仇錄—科技史上的十大爭端」一書，特地把十多年前另一本談科技發展的「想像的未來」拿出來溫習溫習，對照呼應一番，曾經從青少年就熱衷天馬行空的思緒，像是對科技世界的總問細問，一股腦地湧現。這讓人有一種又喜又嘆的感覺。喜的是難得近年看到一本書主要就是細談科技發明與科學發現的故事，而且還寫得如此精采並具有戲劇張力；嘆的是經過了這樣多少有一些歷史考究的「內幕揭發」，我們對於創造發明的偉大夢想不免再次蒙上一層灰暗，但也許這正是現實的光亮之處！正如套用改編自電影「三不管地帶」當中那則吊詭笑話的說法：悲觀與樂觀有什麼不同？看待「現在文明科技好不好」的這個問題時，悲觀的人認為情況不會更好(現在已經是最好的？)，而樂觀的人認為會！

「科技恩仇錄」所開啟的省思，大致上可以從兩方面來說。一方面就是現實人生，從機器是問題的所在嗎？奈德･勒德對抗工業革命、是誰發明礦工安全燈？戴維單挑史蒂文生、到底誰發明了電磁電報？摩斯對抗傑克遜和亨利、交流電∕直流電之戰：愛迪生對抗西屋、汽車製造業的大「車」拼：福特對抗塞爾登及持有執照汽車製造商協會、第一架成功的飛行器：萊特兄弟對上了寇提斯、查努特、艾達、懷德海等人、「電視之父」名歸何人？薩諾夫對抗方斯渥斯、核子潛水艇和核子海軍何去何從？瑞克歐弗對抗宗華特、「人類基因組解密」計畫途徑抉擇？凡特對抗柯林斯一直到生物技術領域中的戰鬥：雷夫金對孟山都公司，夾雜著新仇舊恨、合縱連橫，沒有一個故事不精采，沒有一段劇情不生動，這些在人類科技發展與發明史上扮演舉足輕重的A咖，其實一樣有著凡夫俗子的意念個性與愛恨情仇，甚至這些意念個性與愛恨情仇，才是決定文明發展的關鍵因子。不免讓人想到「天下熙熙，皆為名來；天下攘攘，皆為利往。」這典故：在《清代皇帝秘史》記載乾隆下江南時，來到江蘇鎮江金山寺，看到山腳下大江東流，船來船往，人聲鼎沸，熱鬧非凡，便問旁邊一老和尚：「你在這裏住了幾十年，可知每天來來往往有多少船？」老和尚說：「我只看到兩隻船，一隻為名，一隻為利。」這種簡說，顯然也把文明故事說完了一大半。而務實地說，如果創造發明途徑拒斥名利，那發展難逃艱困而貧乏，但如果創造發明之道是為追求名利，那命運註定紛亂與空虛。

另一方面是整體人類科技文明發展上的，上述還只是「科技恩仇錄」提到了事例，實際上許多在創造發明的「分歧」，像是「資料儲存格式與器材」、「飛機VS.飛船」、「鍵盤設計之爭」、「核分裂核能VS.其他能源」一直到「作業系統軟體之爭」、「網路開放系統VS網路封閉架構」…林林總總的競爭、消長、分合、興衰、演變如火如荼，方興未艾！物理學家戴森認為：「科學革命有兩種形式，一種由新工具引發，另一種由新觀念引發。孔恩在他的名著『科學革命的結構』中講的，幾乎全都只限於觀念革命，差不多完全沒提到工具革命。…孔恩那本大作寫得實在太精采了，因此很快就成為經典之作。然而，它卻誤導了一整個世代的學生以及科學史學者，讓他們誤以為，所有科學革命都是由觀念所引發的。觀念驅動的科學革命一向最富吸引力，而且最能衝擊社會大眾的科學認知，但是，他們其實是比較罕見的。

就拿最近五百年來說，除了被孔恩選為例證模型的量子力學革命之外，科學史上就只剩下六場主要的觀念驅動革命，分別和哥白尼、牛頓、達爾文、馬克士威、佛洛伊德以及愛因斯坦有關。然而，同樣這五百年內，大約出現了大約二十場工具驅動革命。社會大眾對這些工具驅動革命，沒有留下那般深刻的印象，但它們對於科學的發展，卻是同等重要。兩個工具驅動革命代表：第一個是天文學上，由於使用望遠鏡而產生的伽利略革命；第二個是由於使用X光繞射決定生物體大分子結構，而產生克里克–華森革命。」並主張：「觀念驅動革命的功效在於，用新的方法解釋舊的事物。反觀工具驅動革命的功效，則在於發現需要進一步解釋的新事物。」由此，「人群—工具—發明—思維—驗證—理論」形成的龐大而複雜網路的動態呈現，才是科學革命與文明演進的真貌！

許多主流的科學書籍與教科書多多少少成了化約主義甚至精英權威的信奉者，常常塑造一個所謂「科技文明演進」的「系統」形象，也許版本不同，為了能掌握的方便與條理，把事物發展的脈絡賦予一種理論與邏輯的正當性與必然性，甚而走火入魔者，全然接受「成王敗寇」的價值觀，相信勝出的科技一定有著科學上的「優越性」，存活的文明就是最強的，這樣的論調至少對我個人而言，說服力愈來愈顯薄弱，之所以還沒有完全消除，只是因為在「優」與「強」的文辭解釋上還有讓度的空間！雖然一種「好的」科技發展大致上要符合附有彈性、可驗證、輸得起的條件，但是否能出類拔萃、發光發熱、可長可久，其實「因緣際會」還是最精煉的解釋！

無論是「科技恩仇錄」採用的史料鋪陳，或是「想像的未來」專業的評論批判，當中也涉及兩個令人感到相當熱血的課題—科幻與發明，也都滋養了靈感與發想的沃土。舉例來說，對現實文明與主流科技的批判，並不代表就要採取一種憤世嫉俗的姿態，甚至絕非等同貴古賤今的情迷，反而促成了一種超越「科技樂觀主義」的樂觀，而這種樂觀是需要智慧、反思與希望的！在當中，我們的批判是為了反省教訓，我們的冀求是為了珍惜當下，我們的精進是為了利益眾生。單把過去、現在、未來科技發明的合理可能性作一系列的排列組合，從創作想像到現實發展都足以從「無奈」過渡到「無限」！

我真正想談的平行現實與分歧世界，並不是甲國與乙國，A族與B族，甚至不是軸心與同盟那樣歷史存在的有限格局，我要談的，是從科技科學創造發明的角度，一種「不同文明的模樣」，一種「人類發展的可能性」！「決定論」的科學觀也許真的很難自圓其說，但當中又存在著什麼道理具有強大的吸引力，就像電影「大隻佬」中提到：「我說的因，不是你們說的因；我說的果，也不是你們說的果！」看到這些可信度很高而且細膩的科技故事，可以提醒我們其實真正上並不存在所謂「完全客觀的科學與科技」，它們的發展當然也一樣，就像「測不準原理」所支持的那般，森羅萬象的發動者、參與者與觀測者、描述者總是密不可分的，另一種要說，當然就是「一切法由心想生」。那麼，少一點的恩仇，多一點的想像，科技的未來會是怎麼樣？

本文原發表於想趣時空[2011-09-08]
歡迎造訪創發社CAIV

大學新鮮人通常是戀愛解禁的時刻，但如何抉擇愛情，是許多莘莘學子一生的困惑。許多人喜歡對他人的感情做出評論，但似乎沒有人使用科學或心理學的方法來討論。這個問題在歐美地區一樣很常見，高中生情侶上大學後分隔兩地，第一次回家過感恩節假期，之後往往就會分手，俗稱為「火雞分手」（Turkey drop，如果你很好奇拿這個辭去Google，你會發現很多有趣的事）。

若將這件事情說的更科學一點，我們可能要換個說法：如果我們遵守連續單偶制（指一人有許多配偶，但每次只有一個），那要跟多少人在一起過，才能知道誰最適合你？

此一困境在數學心理學（Mathematical psychology）上已經研究多年。數學心理學屬於認知心理學的次領域，是使用數學模型來討論心理學所遭遇的各種問題。如何在最佳時機作決定，稱為「最佳停止點」（或稱「最佳停止問題」，Optimal Stopping）〔1］。「最佳停止點」可以應用的方向很廣，舉凡需要做抉擇的事情，都可以用此方法來思考，小到午餐要吃什麼、找停車位、找旅館，大到面試新人、租房子、買賣房子、決定人生伴侶等等。

這個問題已經有了最佳的解答，就是 37﹪法則。

什麼意思？就是將願意花掉的總時間乘以 37﹪，就是最佳決定的時刻。舉一個簡單例子，如果你想要在兩個月之內租到房子，那個房子是最佳房子的最佳機率。那就把 60 天乘以 37﹪，也就是 22 天。也就是花了 22 天之後，你就要出手了。只要找到比你先前看過的房子更令人心動的房子，就立刻動手，不要猶豫，這就是最佳決定的時間點，因為你花再多時間也不可能找到更好的了。

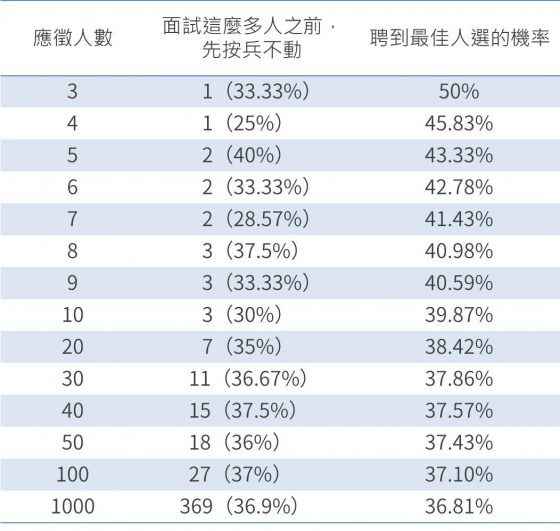
秘書問題：以最少的時間面試，找到最佳的人選

為什麼是 37﹪，而不是其他數字，這是一個嚴謹數學的問題。「最佳停止點」源自一個古老的起點稱為「秘書問題（secretary problem）」：我們希望花最少的時間，找到最佳的人選。最佳的解決方案，是設定一段思考時間，在這段時間中，先不錄取。但過了這段時間，只要看到比思考階段更好的人選時，就馬上錄取。

如果我們逐一將面試的幾人之後，就做出決定，依序可得到表一。面試兩人時，不論錄取誰，成功率都是 1/2（兩人各有一半的機率是最佳人選）。如果有三人應徵，情況變得較為複雜。在面試第一人，先按兵不動。面試第二人時，若我們知道他比第一位好，就先錄取；若比第一位差，就不錄取。如此找到最佳人選的機率，跟應徵兩人時是一樣的，也是 1/2^註。

當可選擇的人數越來越多時，做決定的界線就是 37﹪。採用這個策略，找到最佳人選的機率也趨近 37﹪。沒錯，世界上並不存在最完美的策略，就算是我們覺得這是最好的方法了，其失敗率仍有 63﹪。採取這樣的方法，主要是取決於大多數的情況下，我們都無法找到最佳人選；但最佳停止策略，卻幫我們節省最多的時間。

回到決定人生伴侶這件事也是雷同的。37﹪法則不只用在應徵人數，也可用在尋找時間。假設從 18 歲開始，我們就汲汲營營於尋找另一半，至 45 歲左右為止。那依據最簡單的減法與乘法（〔（45-18）+1〕×37﹪＝10.36），那決定終身伴侶的時間點，就是落在 28 至 29 歲之間。如果那時你已經有合適的伴侶，那就可以考慮結婚了，因為以後也找不到更好的了。（假設啦，我知道真實的情況是像下圖這樣XD）。

面對七嘴八舌的詢問，就「解釋」給他們聽吧！

如此之結果，就是對於大一新生伴侶，最好的解答。他們根本不用在十八歲就做人生最後的決定，最佳最合適的時間點根本還沒到。如果遇到惱人的三姑六婆，我們可以拿出數學慢慢算給他們聽，以他們對於數學的耐受力，肯定三分鐘後就放你一馬了。（因為根據 37﹪法則，他們對於困難數學的問題最多只能聽十分鐘，他們能撐三分鐘，已經是最佳策略了）。

其實這個解決方法十分好用，很多時刻時我們常常不知如何做決定，包括買東西、找車位、訂機票、訂旅館等等，難以抉擇的當下無時無刻的困擾著我們。這時候，想想人生並不存在 CP 值最高的，而是「最佳停止點」，才是最完美的策略，想必對於困境也就能慢慢釋懷了。

• 註：因為三位應徵者，若依其優秀程度，有六種排列方式：1-2-3、1-3-2、2-1-3、2-3-1、3-1-2、3-2-1。若依上面所述，面試第一人先不動。接著只要有更好的人選就錄取，這樣成功錄取最優秀的排列為2-1-3、2-3-1、3-1-2，佔全體一半。若是另外三種排列方式1-2-3、1-3-2、3-2-1，一樣有一半的機率錯過最佳人選。

參考資料與延伸閱讀：

1. 甘錫安（譯）（2017）。決斷的演算：預測、分析與好決定的11堂邏輯課（Brain Christian & Tom Griffiths）。新北：遠足文化。