- 執行編輯|林婷嫻
美術編輯|張語辰
人生由一連串「選擇」組成,不同選擇會導致不同結果。如何衡量人們的抉擇對後果有什麼影響?這是經濟學家感興趣的命題。「衡量」總要有個客觀且避免偏誤的計量方法,而本文專訪中研院經濟研究所的許育進副研究員,專門設計給經濟學家使用的「統計方法」。

「通常跟親朋好友說我是研究經濟學的,接下來他們就會問我:要買哪支股票?」許育進笑說大家對於經濟學的印象,而這背後也反映出一個人性──人們對於「選擇」的猶豫,以及希望能預測「選擇的後果」。
每天睜開眼,人們就面對不同的選擇題。有些選擇的後果無傷大雅,有些卻讓人懊悔「千金難買早知道」。這看在經濟學家許育進的眼中,是非常有趣的研究題材。
人們有沒有做某件事?對結果有多少影響?我們試圖設計方法來衡量。
如何衡量「有做」和「沒做」對結果有多少影響?
這是計量經濟學中,「處理效果」探討的問題。「有做某事」和「沒做某事」對結果有多少影響?這中間的影響差異,就是經過某個行為「處理」之後的效果,統計上可透過平均數(mean)、分佈(distribution)、分位數(quantile)等量化資訊來呈現。
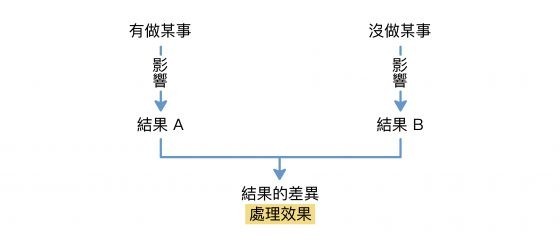
其實,處理效果(treament effect)最早源自於藥學,比較「有吃藥的病人」和「沒吃藥的病人」,對於病情影響的顯著差異,藉以了解某種藥物(treament)治療後有沒有效果(effect)。這個概念現在普遍應用於計量學領域,可用來比較「平行時空」中人們選擇採取某種行為後,產生的結果差異。
研究「處理效果」主要困難之處、跟解決方法?
例如,若想研究「一個人有沒有讀大學」對於「未來的收入」有沒有影響,就得比較「一個人有讀大學」和「同一個人沒有讀大學」的收入差異。
但現實世界中,我們不可能同時踏上兩條人生路徑,存在選擇方案 A 的我,就不存在選擇方案 B 的我。因此,我們分析的樣本資料中,只會看到同一人的其中一種狀態(有讀大學/沒讀大學)、與現在的收入區間。
這是研究處理效果最困難的地方──如何推測「平行時空」中另一種結果?

生命科學研究中,可透過隨機試驗(random assignment)來推估樣本資料、得到分析結果,然而經濟學無法使用隨機的統計方法。因為「有沒有讀大學」在真實情況中並非丟銅板隨機決定,而是受到許多「解釋變數」影響所做出的選擇,例如家庭經濟狀況、父母教育程度等等。
因此,我們的統計方法是先控制這些解釋變數後,再找出個人特徵相近的樣本(例如:家庭年收入相當、父母教育程度相同等等),作為平行時空的對照組──也就是「做出另一個選擇的我」,藉此推估對照組的收入區間,再統計分析兩組收入的差異,如下圖所示。
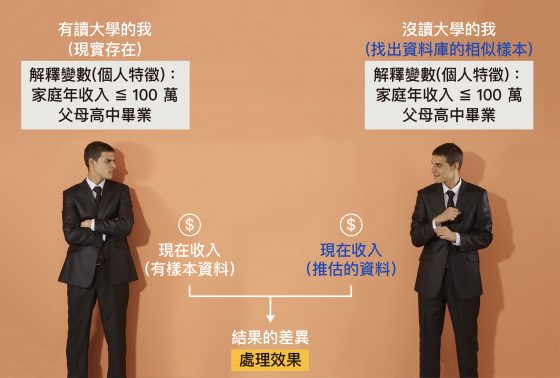
們的這種統計方法,可以用來回答很多關於「選擇結果」的問題。例如,媽媽第一胎懷孕期間有沒有抽菸,對新生兒的體重是否有影響?我們的實證研究加上「孕婦的年齡」做比較,分析結果顯示:孕婦的年齡越大,懷孕時吸菸對於新生兒的負面影響越顯著,也就是新生兒的平均體重會變得越輕[1]。
另外,處理效果的統計方法,也可運用於檢視社會福利政策的效果,例如,我們分析 National Supported Work Demonstration(NSW)職業培訓資料,來探討「有沒有參加職業培訓」會否提升未來收入?
我們的實證結果顯示:「有參加職業培訓的我」工作收入確實會比「沒有參加職業培訓的我」還高[2]。必須說明的是, NSW 資料庫裡的樣本是較難就職的族群,包含貧困家庭的媽媽、年輕輟學者、更生人等等,並非指大眾勞工或上班族。
回到親朋好友的提問,經濟學家知道要買哪支股票嗎?
我們設計的統計方法,可以從多個投資組合中,找出哪個投資組合會賺錢。
例如,若想知道 100 支股票中,哪一支股票會賺錢。那我們就設定 H0 虛無假設為:「這 100 支股票中,有一支股票的利潤平均數 ≤ 0,或是 ≤ 自訂的標準數值(benchmark value) 」,接著統計檢定這 100 支股票的資料,看看哪支股票的檢定結果「拒絕」這個 H0 虛無假設,就是會賺錢的股票,因為它的利潤平均數是 > 0,或是 > 自訂的標準數值。
需注意的是,這統計檢定過程很容易產生偏誤,也就是 data snooping bias。
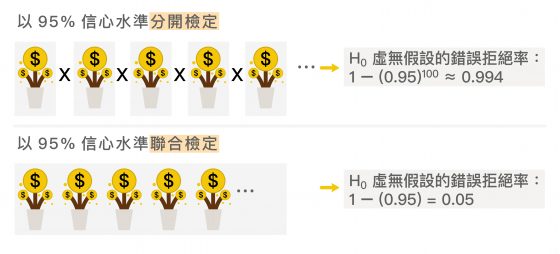
例如,若把 100 支股票的資料分開 t 檢定,且每次 t 檢定都是以 95% 信心水準執行的話,100 次 t 檢定累計高達 0.994 的機率會與實際結果有偏差,這就產生了一種統計偏誤的問題(data snooping bias)。用白話文來說,這問題可能是把其實不賺錢的股票,錯當成會賺錢的股票。
如果研究題目是:「100 支股票中,哪一支股票會賺錢」,這種關於「搜尋」的題目,就得同時考慮好幾百個假設和變數,為了得到較健全(robust)的結果,需改成聯合檢定(joint test)的統計方法。
以實際案例來說,與管中閔教授及許博炫教授討論後,我們參考 stepwise Reality Check test(Romano and Wolf, 2005),改良為 stepwise SPA test 這種可以在多個選項中逐步測試的聯合檢定法,用來回答「從多個投資組合中,搜尋哪個投資組合會賺錢」這種問題。我們套用這個方法分析成長和新興市場的指數股票型基金(ETF),用來佐證某些交易策略(technical trading rules)是否確實可以預測 ETF 的走勢 [3]。
另外一個案例,呂宗勳副教授及陳奕奇副教授發現,當 K 線(Candlestick chart)的股票價格走勢出現某種模式,就可預測接下來應買入、或賣出該支股票。呂宗勳副教授希望能用嚴謹的統計方法,來檢定這種 K 線投資策略會不會賺錢,所以找我們合作,而實證結果也顯示真的會賺錢。
觀察 K 線的股票價格走勢,可以延伸出很多投資策略,我們將這些投資策略全部一起用 stepwise SPA test 檢定,並控制統計偏誤,詳細的計算過程都發表在論文中 [4],有興趣的朋友可以直接參考。
為什麼會投入經濟學研究?
我其實沒有生涯規劃,只是用「刪去法」避免我不想做的事情。人生這麼短,要做會讓自己開心的事。
高中讀自然組是因為不喜歡社會科目,後來因為對工科、做實驗沒興趣,大學志願就選填數學系。讀臺大數學系的時候,遇到很聰明的同學,如果繼續鑽研數學理論,我知道我不可能贏得了他們。大二時看到有些朋友選修臺大管理學院的課,我想試試看自己是否感興趣,就開始修經濟和會計。
經濟學非常有趣,在很好玩的假設下,可以得到這世界大部分的結果。
經濟學有一說,假設每個人都有理性,會在有限資源內做出效用最大的行為。其實這蠻貼近我們的生活,有多少錢就決定做什麼事。假設我只有一千元,我會在這一千元的範圍內,決定要先吃冰、買衣服、還是看電影,做出會讓自己最開心的決定。
研究經濟學的「統計方法」有何困難?
計量經濟學領域中,很多學者在不同的條件假設下,進行不同的研究題目,運用不同的統計方法來計算。
我會專門研究給經濟學家使用的「統計方法」,這跟我的數學背景有關。通常我是找一個已經整理好的樣本資料,看看我設計的統計方法,分析這些資料能否回答新的問題;或是同一套統計方法,應用在不同資料庫,會分析出什麼樣不同的結果。 internetinių svetainių ir el parduotuvių kūrimas, reklama internete ir SEO paslaugos
最困難的是找到大家感興趣的問題,以及找到可以使用的數學工具。
研究新的問題時,不見得有現存的數學工具可直接套用,甚至有時候看不出來哪個數學工具可以引用。有時候我們大概的想法都有了,但困難在於要想辦法把中間的理論證明補齊。

如何突破研究沒進展的困境?
當然,理論證明不出來的時候,會很失落、很煩,需要做可以放鬆的事情。我在美國讀書的時候,是透過煮飯暫時脫離研究上的不愉快。從買什麼菜、怎麼處理、到看到成品,這過程都要專心,因為若分心,切菜時可能會切到自己。
回臺灣後我改做羊毛氈,這也需要很專心,不然針會戳到手。這些羊毛氈有些送給朋友,有些會義賣並捐給流浪動物花園。

研究上突破瓶頸的方式,我也會找熟悉的人討論,看看有沒有已知的統計方法可以使用,或有類似的文獻可參考。或找他們一起合作。另外,當想出某個研究題目,但不確定這個題目有沒有人感興趣,也可以先問問相關領域的學者。
與其自己想不出來,多跟別人討論比較有用。
注解:
- Jason Abrevaya, Yu-Chin Hsu and Robert P. Lieli(2015), “Estimating Conditional Average Treatment Effects,” Journal of Business and Economic Statistics, 33 485-505.
- “Estimation and Inference for Distribution Functions and Quantile Functions in Treatment Effect Models,” Journal of Econometrics, 178, 383-397, 2014 (joint with Stephen G. Donald).
- “Testing the Predictive Ability of Technical Analysis Using A New Stepwise Test without Data Snooping Bias,” Journal of Empirical Finance, 17, pp. 471-484, 2010 (joint with Po-Hsuan Hsu and Chung-Ming Kuan).
- Tsung-Hsun Lu, Yi-Chi Chen and Yu-Chin Hsu(2015), “Trend Definition or Holding Strategy: What Determines the Profitability of Candlestick Charting?,” Journal of Banking and Finance, 61 172-183.
參考資料:
本著作由研之有物製作,原文為〈衡量「人生的選擇結果」有方法──專訪許育進〉以創用CC 姓名標示–非商業性–禁止改作 4.0 國際 授權條款釋出。
本文轉載自中央研究院研之有物,泛科學為宣傳推廣執行單位
在網站上看不過癮?研之有物出書啦!
《研之有物:穿越古今!中研院的25堂人文公開課》等著你來認識更多中研院精彩的研究。