證明「費馬最後定理」：懷爾斯生日│科學史上的今天：4/11

數感實驗室／朱倍玉

如果有人突然問你： \(  a^{2}+b^{2=} \)？ 台灣學生大概像膝反射一樣，自然而然地答出 \( c^{2} \)。

直角三角形，直角的兩鄰邊長的平方和等於斜邊長的平方。這是人人都熟悉的畢氏定理，也是百年數學之謎「費馬最後定理」的一部分。

費馬提出的世紀難題

費馬（Pierre de Fermat）是 17 世紀的一名律師，數學是他業餘的興趣，當時與他書信往來的包括了笛卡爾、帕斯卡、惠更斯等歷史上知名的數學家。雖然費馬本業跟數學天差地遠，但他相繼提出微積分、機率論與數論的研究，在數學界的貢獻不輸職業數學家，也因此獲得「業餘數學家王子」的封號。

研究《算數》（Arithmetica）這本書時，費馬在書的空白處寫下「\(  a^{n}+b^{n}=c^{n} \)，當 \(  n>2  \) 時無正整數解」，並且用拉丁文留下一句話「我發現了一個極為美妙的證明，可是空白處太小所以沒寫下來」。

短短一條小學生就能理解的式子，再加上一句話，卻讓後世的數學家們花了足足三百年，直到 1995 年才由懷爾斯（Andrew John Wiles）教授完成證明，而這項證明，被稱為上個世紀的大任務。

(2019/8/20) 編按：原文提及費馬定理時敘述為「無解」，實為「無正整數解」，特此更正。

立志要趁早，十歲許願解題的懷爾斯

這個世紀大任務的起點是懷爾斯 10 歲那年。他在圖書館翻閱一本講述費馬最後定理歷史的書，當時，他便對費馬留下來的難題產生濃厚興趣。在其他人才正要認識三角形的年紀，懷爾斯已經下定決心要解決這道流傳百年的難題。正好，又提供大家一個立志要及早的偉人例證。

跟很多成就大事的人一樣，懷爾斯在研究費馬最後定理的過程並非一帆風順。他踏入數學界的時期，正好是數學界準備放棄費馬最後定理的時候。大多數學家認為費馬最後定理無法證明，紛紛轉往其他領域。懷爾斯的指導教授也不例外，要懷爾斯放棄夢想，別白忙一場。也因此除了夢想外，他同時開始研究橢圓曲線^註1這個領域。

然而事實上在更早以前，日本數學家谷山豐和志村五郎提出「谷山－志村猜想」，他們認為橢圓曲線與「模形式」^註2可能有關聯。但是，橢圓曲線或是它與模形式的關聯跟費馬最後定理有什麼關係呢？1985 年，德國數學家佛列（Gerhard Frey）將谷山－志村猜想與費馬最後定理連結，他認為谷山－志村猜想可能可以協助完成費馬最後定理的證明。

後來，法國數學家賽爾（Jean-Pierre Serre）、美國數學家里貝特（Ken Ribet）也投入研究。他們發現只要證明出谷山－志村猜想就可以完成費馬最後定理的證明，才再次啟動懷爾斯的世紀難題證明之路。

於是，長達 7 年的時間，懷爾斯致力於研究谷山－志村猜想與費馬最後定理，他也找來另一位數學教授卡茲（Nicholas Katz）加入研究。懷爾斯是一個很低調的人，為了避免引起眾人的懷疑與關注，他在學校開設新課程，好讓卡茲協助他找到證明費馬最後定理所需要的最後一項工具──類數公式^註3。

由於懷爾斯從未說明開課目的，也沒向學生解釋這個公式將幫助他們通往費馬最後定理，只是不停地證明，難度相當高，搞到最後台下聽眾就只剩下卡茲。不久後，懷爾斯正式完成所有證明。他選擇在劍橋大學舉辦三場研討會，對外宣稱研討會的內容討論的是橢圓曲線和模形式，完全沒提到費馬最後定理。

當時有些謠言，這場研討會似乎有更勁爆的突破要發生，許多學者因此前來。研討會上，懷爾斯從橢圓曲線、模形式，一路證明到費馬最後定理，帶給台下聽眾滿滿的驚喜。隔天報章雜誌上，到處都在報導世紀難題已經解決的喜訊。

以為解開了嗎？過程曲折離奇

然而「福兮，禍之所伏」，驚喜後面還藏了一個巨大的驚嚇。當懷爾斯的證明手稿進入審查階段，卡茲與懷爾斯反覆驗證時，他們找到一處先前完全沒發現的錯誤。

人們尖銳地檢視著懷爾斯的失誤，漫天的喜訊瞬間化成毫無遮掩的嘲諷。懷爾斯接受訪問時也表達，在備受矚目的狀態下進行研究並不是他的風格。他把自己關在書桌前，試圖解決這個錯誤，然而不論怎麼做都沒辦法突破。

就在陷入絕望之際，他偶然在桌邊看到一份關於「岩澤理論」的論文。一時靈光乍現，他運用了岩澤理論來化解掉原先證明的錯誤，完成證明。1995 年，世紀難題才正式從未竟之謎的名單中消除。

「或許，我能給出關於我研究數學的歷程最貼切的描述，就是進入一棟大房子。當一個人開始探索第一個全黑的房間時，裡頭一片漆黑，他會在家具中邊跌倒邊摸索。漸漸地知道家具的位置。六個月後，你會找到開關並且打開燈。開燈的那一瞬間，整個房間被光線壟罩，你終於，能清楚地看見你站在哪裡」

——懷爾斯（Andrew John Wiles）

BBC拍攝了一部關於破解費馬最後定理的紀錄片，這段話正是懷爾斯在片頭的開場白。

破解費馬最後定理的世紀任務就像是完成一場接力式的拔河比賽，仰賴歷史上許多數學家的一臂之力，更需要在時間的沖刷與眾人的關注下承擔壓力的決心。從這個例子我們也可以看到，數學不是計算，更不是算得快就叫數學好。它是思考與邏輯，能讓許多人投入一生也樂此不疲的遊戲。

今年的 8 月 17 日，正好是費馬的 418 歲生日，特別寫這段費馬留給後人的禮物來祝他生日快樂！

註釋：

1. 橢圓曲線（Elliptic Curve）是二元三次曲線的一種形式，其圖形並非橢圓，而是圓環狀。
2. 模形式（Modular forms）是具有極複雜對稱性的複數平面函數。
3. 類數公式（Class number formula）與環的有限序列有關。

資料來源：

• 費瑪最後定理（Fermat’s Last Theorem） 紀錄片
• mathworld.wolfram-Elliptic Curve
• 模形式
• mathworld.wolfram-Class Number Formula
• 解開「費馬最後定理」的懷爾斯—《科學月刊》
• Andrew John Wiles
• Andrew-Wiles
• Pierre de Fermat

作者｜李武炎／曾任教於淡江大學數學系，現為《科學月刊》編輯委員。

今年素有「數學諾貝爾獎」的阿貝爾獎由美國牛津大學皇家協會講座教授懷爾斯（Andrew Wiles）獲得，推薦文中指出，為了表彰他利用半穩定橢圓曲線的模猜想推出「費馬最後定理」的震撼證明，對數論的發展開啟一個新的世代，獎項已於今（2016）年 5 月 24 日在挪威首都奧斯陸頒發。

英年早逝的天才數學家阿貝爾

阿貝爾（Niels Henrik Abel，1802~1829）是挪威歷史上一位非常著名的數學家，他在很年輕的時候就已經研習大數學家歐拉、拉格朗治、拉普拉斯及高斯等人的著作。19 歲時，他解決了困惑數學界 200 年的老問題：一般 5 次方程式根的公式解是不存在的，如此非凡的表現奠定他在歷史上的地位。另外他在超越函數上的研究，對橢圓函數理論起了革命性的影響。阿貝爾生前非常貧困，18 歲時就肩負起照顧家中 6 個弟妹的重責，後來不幸罹患肺結核，因為無法得到良好的調養， 很可惜在 1829 年 4 月 6 日以 26 歲的年紀辭世，實在是英年早逝，死後兩天，數學家克雷勒（August Leopold Crelle） 攜來柏林欲聘請他擔任教授的聘書，但已經來不及了。後來數學界為了紀念他，特別將抽象代數學中的一個結構交換群命名為「阿貝爾群（abelian group）」，以他為名的專有名詞已經被普通化了，是為了更能彰顯他的偉大。

挪威政府一直有設立紀念阿貝爾的獎項的念頭，這是要彌補諾貝爾獎沒有數學項目的遺憾，但這個獎項的成立一直要等到西元 2002 年阿貝爾 200 歲誕辰方才實現。2002 年阿貝爾獎開始頒發，而第一屆的得主便是法國數學家，同時是數學界大老的謝爾（Jean-Pierre Serre）。去年 2015 年的得主是電影《美麗境界》戲中的主人翁約翰納許，但去年 5 月 19 日納許夫婦領取阿貝爾獎返家途中不幸發生車禍遇難，曾造成新聞界一陣報導。觀察阿貝爾獎的歷屆得主，都是當代數學的翹楚， 而且大都是年高德劭著作等身的數學圈耆老，懷爾斯雖屬壯年，但因為他解決「費馬最後定理」這個世紀難題， 名氣實在太大了，因此阿貝爾獎的評審委員會決定頒授 2016 年的獎給他。有人說這是遲來的獎項，因為自從 20 幾年前懷爾斯證出這個劃時代的問題後，已經得獎無數，幾乎全世界所有的數學獎都被他囊括，其中包括著名的沃爾夫數學獎（1995 年）、沃爾夫斯克爾獎（1997 年）以及邵逸夫獎（2005 年）等，今年添上阿貝爾獎無疑是在懷爾斯的功勛簿上貼滿最後一塊拼圖。值得一提的是，當年懷爾斯解決費馬最後定理時已經年過 40， 無緣獲得數學界的費爾茲獎章（Fields Medal）。

 費馬最後定理

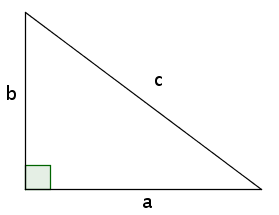
「費馬最後定理」是個一般人都可以明瞭的題目， 並不需要具備很深的數學背景才能理解──探討方程式： xⁿ+yⁿ=zⁿ 的正整數解。當 n = 2 時， 讓我們想到熟知的畢氏定理（又稱勾股弦定理），此處 z 代表一個直角三角形的斜邊長，x 與 y 則為此三角形之兩股的長，也就是說一個直角三角形的斜邊長的平方等於它的兩股長之平方和。 這個方程式當然有許多正整數解，例如：x = 3，y = 4，z = 5；x = 6，y = 8，z = 10；x = 5，y = 12， z = 13 ⋯⋯等等。費馬聲稱當 n ≥ 3 為正整數時， 就不存在非零的整數解。

數學業餘王子─費馬

費馬（Pierre de Fermat，1601~1665）是一位留著長髮，穿著中古世紀歐洲袍的法國數學家。他是 17 世紀最卓越的數學家之一，在許多數學領域都有極大的貢獻，例如：他在笛卡兒之前發明解析幾何，也在微積分的發展有所建樹，他與巴斯卡被公認是機率論的先驅， 然而他在數論上的研究成果最為後人所記得。他的本行是專業的律師，數學只是他的愛好，而他所作的數學作品都是第一等的工作，為了表彰他的數學造詣，世人冠以「業餘王子」的美譽。在 1637 年的某一天，費馬正在閱讀一本古希臘時代數學家丟番圖（Diophantus） 的數論書《算術學》（Arithmetica）時，突然心血來潮在書頁的空白處寫下這個看似簡單的定理：當 n ≥ 3 為正整數時， 沒有非零的整數解。

當時費馬並沒有說明原因，不過他留下這一段話：「我已經發現一個非常美妙的證明，只是書頁的空白處太小無法寫下來。」，始作俑者的費馬也因此留下了這個千古的難題，300 多年來無數的數學家嘗試要求解決這個難題都徒勞無功，這個號稱「世紀難題」的「費馬最後定理」也就成了數學界的心頭大患，極欲解之而後快。19 世紀時法國的法蘭西學院曾二度懸賞金質獎章及 300 法郎給任何解決此一難題之人，可惜都沒有人能夠領到獎賞。德國的一位工業家沃爾夫斯克爾（Paul Wolfskehl，1856~1906）對「費馬最後定理」情有獨鍾，他死後，根據其遺囑遺贈 10 萬馬克（約合 5000 萬新臺幣），頒給能夠證明「費馬最後定理」是正確的人。

這個獎在 1908 年設立，有效期間為 100 年，懷爾斯在 1997 年領到這個獎時，獎金只有約 150 萬新臺幣， 原因是這段期間世界曾發生經濟大蕭條，此筆獎額已大幅貶值了。當年沃爾夫斯克爾獎一宣布時，確實吸引不少「數學癡」去從事這個問題，而社會上也掀起了一股瘋「FLT（Fermat’s Last theorem）熱」。20 世紀電腦發展以後，許多數學家利用電腦計算可以證明這個定理當 n 很大時是成立的，1983 年電腦專家斯洛文斯基借助電腦運行 5782 秒證明當 n 為2⁸⁶²⁴³-1 時「費馬最後定理」是正確的，2⁸⁶²⁴³-1是一個天文數字， 大約有 25960 位數。雖然如此，數學家還是沒有找到一個普遍性的證明。不過這個三百多年的數學懸案終於解決了，由當時在美國普林斯頓大學數學系任教的英國數學家懷爾斯教授提出證明，其實他是利用 20 世紀過去 30 年來代數幾何發展的結果加以運用並解決的。

追求數學聖杯的懷爾斯

1993 年的 6 月 21~23 日，懷爾斯在英國劍橋大學所舉辦的研討會發表這個結果，這個報告馬上震驚了數學界甚至於一般社會大眾，懷爾斯證出費馬最後定理的消息在 1993 年的 6 月 24 日登上了《紐約時報》、《美國國家廣播公司》等重要媒體的頭條。一個數學證明能讓新聞媒體如此青睞，可謂空前絕後，原因正如前面所言，這是一個能被一般民眾所能明白的數學問題，並不需具備很強的數學專業知識。其實數論中有很多問題都與費馬最後定理一樣，敘述都很淺顯易懂，內容也很吸引人去思考，可是證明起來都很難。懷爾斯在 1993 年發表的論文報告經過數學界審慎檢查後，卻發現了極大的瑕疵，後來懷爾斯與他的學生嘗試加以補救，終於在 1994 年 9 月修正成功，並且在 1995 年將修正後的論文發表在《數學年刊》（Annals of Mathematics）上。

偉大的集體成就

「費馬最後定理」的最終解決其實要歸功於無數數學家的努力，最早在 1950 年代，日本數學家谷山豐首先提出一個有關橢圓曲線的猜想，即二元三次方程式 y²=x³+ax²+bx+c 定義的圖形，其中 a、b、c 為有理數，它不是橢圓，而是因為當初數學家想計算橢圓的周長而產生的名詞。後來由另一位日本數學家志村五郎加以發揚光大，提出谷山 – 志村猜想：每一個橢圓曲線都具有一種模形式（modularity pattern）， 這個名詞與高等數學複變函數論有關，在此就不擬加以解釋。當時沒有人認為這個猜想與「費馬最後定理」有任何關聯，直到 1980 年代，德國數學家佛列（Gerhard Frey）才將這個猜想與「費馬最後定理」掛勾。若對奇質數p而言， a^p+b^p+c^p 有異於零的整數解，則佛列建議考慮橢圓曲線 y²=x(x+a^p)(x-b^p)，此曲線後來被稱為佛列曲線， 因為他覺得此橢圓曲線的判別式 a^2pb^2p(a^p+b^p)²=(abc)^2p 呈現出一點不太尋常，因此他懷疑這個橢圓曲線不具模形式，所以只要能證明谷山 – 志村猜想就等於證明了「費馬最後定理」。

佛列的猜想後來被法國數學家謝爾加以改良，並且在 1986 年由數學家里貝特（Ken Ribet）證明從 a^p+b^p=c^p 所得的佛列曲線違反模形式。根據里貝特的這個啟發，懷爾斯就全力去從事谷山 志村猜想的證明，至少要證明絕大部分的橢圓曲線都具有模形式。最後他證明了任何半穩定（semistable）橢圓曲線都具有模形式，而佛列曲線就是一個半穩定橢圓曲線，因此證明 a^p+b^p=c^p 之非零整數解是不存在，從而證明了「費馬最後定理」。這裡要提一點，「費馬最後定理」是說對任何大於 2 的整數 n 而言，aⁿ+bⁿ=cⁿ 沒有非零的整數解，其實就是要證明對 n = 4 及任意奇質數（3、5、7⋯）均成立即可，因為對任何大於 2 的整數 n，n 必有 4 或奇質數的因數，而當 n = 4 時，費馬曾經給予證明（用數論的技巧就可以證出），因此只需考慮 而 p 為奇質數即可。

「費馬最後定理」的證明成功並非僅靠一人之力便能解決，雖然懷爾斯完成了封頂之作，但如同前面所提到的谷山豐、志村五郎、佛列及里貝特都是功臣；自古以來，很多數學理論的形成都是從一些猜想或假設開始，激發數學家的興趣，為了尋求問題的解決，不斷努力發展新的數學技巧，也豐富了數學的內涵，而這些建樹都是歷史上的數學家前仆後繼研究所得的成果，我們可以說：數學演進就是團隊合作的結晶。

〈本文選自《科學月刊》2016 年 7月號〉

延伸閱讀：

數海英雌的孤單與堅強—中研院院士張聖容專訪

數學的諾貝爾獎

什麼？！你還不知道《科學月刊》，我們46歲囉！

入不惑之年還是可以當個科青

兩千多年前畢達哥拉斯發現直角三角形斜邊的平方等於直角兩邊的平方和，於是成了我們每個人應該都背過的畢氏定理：a²+b²=c²；而其中存在許多整數解，例如（3、4、5）、（5、12、13）。那麼三次方以上呢？也可以找到對應的整數解嗎？

1637 年，法國數學家費馬斷定地說沒有！他讀到丟番圖的《算術》一書中畢氏定理的論證時，在附近空白處寫下了著名的「費馬最後定理」：

「另一方面，一個數字的立方不可能表示成兩個立方數的和，一個四次方數也不能表示成兩個四次方數的和；或者更概括性地說，除了平方之外，一個n次方的數也不能表示成兩個n次方數的和（xⁿ + yⁿ = zⁿ）。我已為這個命題找到了一個非常美妙的證明，然而這裡的空間不足以讓我寫下這個證明。」

自此包括大數學家歐拉在內的無數數學家前仆後繼，試圖證明此定理，但直到 1839 年，僅證明 n=3、4、5、7 時成立（n為這些數的倍數時也就當然成立），此後即再無進展（那些用電腦證明的同學不用舉手）。於是這個定理的證明就只有費馬與上帝知道──或者他以為他知道。

沒有人料到這沉寂會在毫無預警的情況下被打破。1993 年 6 月，英國數學家懷爾斯 (Andrew J. Wiles) 在劍橋大學辦了三場演講，事先沒有人知道他要談費馬最後定理，雖然他的題目跟費馬最後定理有些關係，但畢竟之前從未聽聞他在做這方面的研究，大家自然不會作此聯想。直到第二天，參加演講的聽眾才發覺懷爾斯是在談如何攻克費馬最後定理這座高山的登山路線。於是耳語立刻在數學界傳了開來，最後一場演講擠滿了聽眾，內向害羞的懷爾斯果然當場公佈了他完成的證明，令全場為之嘩然。這消息也立刻傳遍全世界，第二天各國的頭版都刊登了這則數學史上的重大事件。

人們才知道懷爾斯已經默默地在這問題上耕耘了七年，除了妻子與一位同事，沒有告訴任何人。然而，懷爾斯的喜悅沒有持續太久；幾個月後他的證明被發現有致命的錯誤，也就是說證明無效！懷爾斯試圖修補這個錯誤，經過一年多的嘗試，就在他打算放棄之際，他改採曾被他丟在一旁的方法，終於取得突破，而於 1994 年 9 月完成證明，並於次年發表。這一次，經過同儕審查完全無誤，高懸三百多年的費馬最後定理終獲證明。懷爾斯也從此在歷史留名。

本文同時收錄於《科學史上的今天：歷史的瞬間，改變世界的起點》，由究竟出版社出版。

「以古為鏡，可以知興替。」如果能在過去、現在兩點拉出一條直線的話，未來的趨勢也有機會在我們掌握之中；當我們遇到困難時可以透過過往的經驗，幫助我們下判斷。這就是歷史的重要性！同樣的，歷史的脈絡可以幫助我們學習科學，而且還有機會發現科學家並不是我們想像中的神聖不可侵。2015 年 12 月 22 日在胖地台北，泛科學的專欄作者張瑞棋帶著《科學史上的今天》，和我們分享科學家背後鮮為人知的小故事。

「從小到大，科學家在我們心中非常偉大，無論是哥白尼的日心說，或者證明地心引力作用一樣的伽利略。這些科學家閃耀著光芒，直到越讀越多書後才發現，光芒的背後其實存在著陰影。這些科學家們的陰影來自信仰、權威以及性別。」

信仰

普遍認為哥白尼的日心說之所以不被認可，是因為宗教的打壓。然而另一種觀點是由於哥白尼認為上帝創造的宇宙應該存在著完美對稱的幾何關係，也就是軌道應該是圓形的！但這會和他觀察到的天文現象不吻合，因此與其說日心說的發表示因為教會的壓力，其實哥白尼本身的執迷才是造成學說延宕的原因。又比如提出滅絕說的居唯葉，他認為物種會因為某些災難而滅絕，另一方面在創世後仍物種繼續被創造。由於他深信聖經的創世論，甚至抨擊達爾文的演化論，導致演化論的發展備受阻礙。

權威

除了信仰外，有時候科學家利用自身權威、堅持己見，抑制別派學說，亦會影響科學的發展。你能想像西元十六世紀，醫生們拿著的解剖經典是出自於西元二世紀的蓋倫，且內容漏洞百出嗎？蓋倫是根據其動物解剖的經驗來推斷人體的內部構造，當然和人體的構造有很大的出入。但許多人不改抵抗權威，使得錯誤流傳千年。直到維薩留斯的出現，人體的結構才終於被了解。維薩留斯憑藉著大量的人體解剖經驗，推翻了多年來的理論，加上他有美術的長才，得以將知識快速的更新、傳播。

另一個為人所知的例子是牛頓及萊布尼茲。在微積分發展上，英國推崇地位較高的牛頓提出的流數，而非萊布尼茲的微積分，這導致英國的數學研究落後其他歐陸國家。最後一個權威造成的悲劇，讓許多產婦賠上了性命。十九世紀，醫生塞默維斯發現由醫院接生的產婦死亡率遠遠高出了由助產士接生的。他推測原因是醫學系的學生在解剖完大體後沒有清潔，而將細菌帶給產婦。然而其他高傲的醫生們認為：醫生怎麼可能害人呢？而摒棄了塞默維斯的想法。

性別

女性在科學界受到的打壓也不少：在代數領域有傑出成就的埃米諾特，竟因其性別而無法擔任大學教授；華生看了羅莎琳．佛蘭克林的 DNA  X 光繞射圖片，終於發現了 DNA 的雙螺旋結構，並以此得到了諾貝爾獎。雖然華生得獎的時候佛蘭克林已過世，然而我們可以想像，在當時的社會氛圍下，即便她在世，女性科學家的得獎機率仍然很低；發現脈衝星的喬瑟琳貝爾其成就在天文界有目共睹，然而諾貝爾物理獎的獎座是被指導教授赫維許拿走；吳健雄透過實驗證實宇稱不守恆，但最後是理論學家楊振寧及李政道是拿到了諾貝爾物理獎。

有些時候科學家對抗的不是來自外界的輿論、權威，反對的力量反而是來自科學界：牛頓打壓虎克及萊布尼茲；愛迪生堅持使用直流電系統，並利用交流電椅製造世人對交流電的恐懼，藉此反對特斯拉的交流電系統；發明氫彈的泰勒對前主管歐本海默落井下石，聲稱歐本海默對美國不忠……

我想呈現的不只是科學家的榮耀，還有其與常人無異的一面

跟著《科學史上的今天》的腳步，我們可以發現科學家或許只在智力上比一般人高超，但其品性仍和常人一樣：他們也會忌妒、也會排擠別人、也會為了得到權力耍手段。如果大家能用平等的角度認識科學家，去了解理論後的時代背景，那學科學就不再只是背公式和定理，而是和一段段生命故事相遇的奇幻旅程。