花了三百年才證明的世紀難題：費馬的最後定理

數感實驗室／朱倍玉

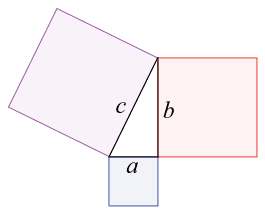
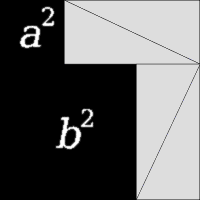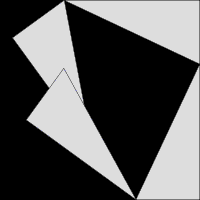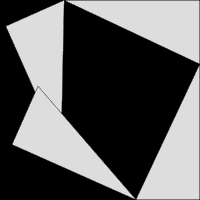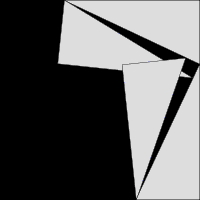
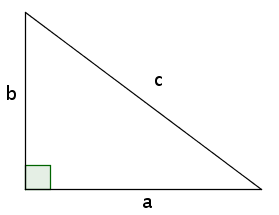
如果有人突然問你： \(  a^{2}+b^{2=} \)？ 台灣學生大概像膝反射一樣，自然而然地答出 \( c^{2} \)。

直角三角形，直角的兩鄰邊長的平方和等於斜邊長的平方。這是人人都熟悉的畢氏定理，也是百年數學之謎「費馬最後定理」的一部分。

費馬提出的世紀難題

費馬（Pierre de Fermat）是 17 世紀的一名律師，數學是他業餘的興趣，當時與他書信往來的包括了笛卡爾、帕斯卡、惠更斯等歷史上知名的數學家。雖然費馬本業跟數學天差地遠，但他相繼提出微積分、機率論與數論的研究，在數學界的貢獻不輸職業數學家，也因此獲得「業餘數學家王子」的封號。

研究《算數》（Arithmetica）這本書時，費馬在書的空白處寫下「\(  a^{n}+b^{n}=c^{n} \)，當 \(  n>2  \) 時無正整數解」，並且用拉丁文留下一句話「我發現了一個極為美妙的證明，可是空白處太小所以沒寫下來」。

短短一條小學生就能理解的式子，再加上一句話，卻讓後世的數學家們花了足足三百年，直到 1995 年才由懷爾斯（Andrew John Wiles）教授完成證明，而這項證明，被稱為上個世紀的大任務。

(2019/8/20) 編按：原文提及費馬定理時敘述為「無解」，實為「無正整數解」，特此更正。

立志要趁早，十歲許願解題的懷爾斯

這個世紀大任務的起點是懷爾斯 10 歲那年。他在圖書館翻閱一本講述費馬最後定理歷史的書，當時，他便對費馬留下來的難題產生濃厚興趣。在其他人才正要認識三角形的年紀，懷爾斯已經下定決心要解決這道流傳百年的難題。正好，又提供大家一個立志要及早的偉人例證。

跟很多成就大事的人一樣，懷爾斯在研究費馬最後定理的過程並非一帆風順。他踏入數學界的時期，正好是數學界準備放棄費馬最後定理的時候。大多數學家認為費馬最後定理無法證明，紛紛轉往其他領域。懷爾斯的指導教授也不例外，要懷爾斯放棄夢想，別白忙一場。也因此除了夢想外，他同時開始研究橢圓曲線^註1這個領域。

然而事實上在更早以前，日本數學家谷山豐和志村五郎提出「谷山－志村猜想」，他們認為橢圓曲線與「模形式」^註2可能有關聯。但是，橢圓曲線或是它與模形式的關聯跟費馬最後定理有什麼關係呢？1985 年，德國數學家佛列（Gerhard Frey）將谷山－志村猜想與費馬最後定理連結，他認為谷山－志村猜想可能可以協助完成費馬最後定理的證明。

後來，法國數學家賽爾（Jean-Pierre Serre）、美國數學家里貝特（Ken Ribet）也投入研究。他們發現只要證明出谷山－志村猜想就可以完成費馬最後定理的證明，才再次啟動懷爾斯的世紀難題證明之路。

於是，長達 7 年的時間，懷爾斯致力於研究谷山－志村猜想與費馬最後定理，他也找來另一位數學教授卡茲（Nicholas Katz）加入研究。懷爾斯是一個很低調的人，為了避免引起眾人的懷疑與關注，他在學校開設新課程，好讓卡茲協助他找到證明費馬最後定理所需要的最後一項工具──類數公式^註3。

由於懷爾斯從未說明開課目的，也沒向學生解釋這個公式將幫助他們通往費馬最後定理，只是不停地證明，難度相當高，搞到最後台下聽眾就只剩下卡茲。不久後，懷爾斯正式完成所有證明。他選擇在劍橋大學舉辦三場研討會，對外宣稱研討會的內容討論的是橢圓曲線和模形式，完全沒提到費馬最後定理。

當時有些謠言，這場研討會似乎有更勁爆的突破要發生，許多學者因此前來。研討會上，懷爾斯從橢圓曲線、模形式，一路證明到費馬最後定理，帶給台下聽眾滿滿的驚喜。隔天報章雜誌上，到處都在報導世紀難題已經解決的喜訊。

以為解開了嗎？過程曲折離奇

然而「福兮，禍之所伏」，驚喜後面還藏了一個巨大的驚嚇。當懷爾斯的證明手稿進入審查階段，卡茲與懷爾斯反覆驗證時，他們找到一處先前完全沒發現的錯誤。

人們尖銳地檢視著懷爾斯的失誤，漫天的喜訊瞬間化成毫無遮掩的嘲諷。懷爾斯接受訪問時也表達，在備受矚目的狀態下進行研究並不是他的風格。他把自己關在書桌前，試圖解決這個錯誤，然而不論怎麼做都沒辦法突破。

就在陷入絕望之際，他偶然在桌邊看到一份關於「岩澤理論」的論文。一時靈光乍現，他運用了岩澤理論來化解掉原先證明的錯誤，完成證明。1995 年，世紀難題才正式從未竟之謎的名單中消除。

「或許，我能給出關於我研究數學的歷程最貼切的描述，就是進入一棟大房子。當一個人開始探索第一個全黑的房間時，裡頭一片漆黑，他會在家具中邊跌倒邊摸索。漸漸地知道家具的位置。六個月後，你會找到開關並且打開燈。開燈的那一瞬間，整個房間被光線壟罩，你終於，能清楚地看見你站在哪裡」

——懷爾斯（Andrew John Wiles）

BBC拍攝了一部關於破解費馬最後定理的紀錄片，這段話正是懷爾斯在片頭的開場白。

破解費馬最後定理的世紀任務就像是完成一場接力式的拔河比賽，仰賴歷史上許多數學家的一臂之力，更需要在時間的沖刷與眾人的關注下承擔壓力的決心。從這個例子我們也可以看到，數學不是計算，更不是算得快就叫數學好。它是思考與邏輯，能讓許多人投入一生也樂此不疲的遊戲。

今年的 8 月 17 日，正好是費馬的 418 歲生日，特別寫這段費馬留給後人的禮物來祝他生日快樂！

註釋：

1. 橢圓曲線（Elliptic Curve）是二元三次曲線的一種形式，其圖形並非橢圓，而是圓環狀。
2. 模形式（Modular forms）是具有極複雜對稱性的複數平面函數。
3. 類數公式（Class number formula）與環的有限序列有關。

資料來源：

• 費瑪最後定理（Fermat’s Last Theorem） 紀錄片
• mathworld.wolfram-Elliptic Curve
• 模形式
• mathworld.wolfram-Class Number Formula
• 解開「費馬最後定理」的懷爾斯—《科學月刊》
• Andrew John Wiles
• Andrew-Wiles
• Pierre de Fermat