- 文/Larrie Ferreiro and Alexander Pollara(譯者:林中一 教授,編修:余海峯 博士)
19 世記約翰・史考特・羅素(John Scott Russell)的船舶設計理論承諾了速度、亦表現了優雅。然而,最終證實那個理論並不完整。
今天的船舶設計師們仍運用 1800 年代末期英國工程師威廉・傅如德(William Froude)所發展出的比例定律來預測船舶的速度與動力。但是遠在傅如德之前,船舶設計者與造船者就已經知道,船體架構或船殼比例與形狀會影響船在水中的速度,而且他們已經找出了支配那些關係的規則。

在 1500 年代末,一位名叫馬修・貝克(Mathew Baker)的英國造船者曾流傳了出一張讓他出名的素描。在這張素描中,他把一隻有著鱈魚鈍頭和鯖魚錐形尾巴組合的混種魚圖像重疊在一艘伊麗莎白時代的軍艦船殼圖上。在當時缺乏任何科學或實驗的基礎之下,這種「船殼的形狀應該由自然原理來支配」的想法仍然被廣泛接受。
貫穿整個 17 與 18 世紀,科學革命孕育了有關流體力學和阻力的新概念,這些概念定義了船舶在水中行進時所受的阻力。由於想要建造更快的風帆動力戰艦,歐洲各國海軍委託了科學家與發明家們去測試這些概念。1800 年初期,蒸汽動力用於在航海,其財務考量帶來了一個將流體阻力降到最低的額外動機:一艘蒸汽船的煤炭消耗量是直接關係到其運轉成本的,而煤炭的消耗就取決於受到的阻力。早期的蒸汽動力船隻比風帆動力的要快也更為可靠,然而它們的引擎效率並不好。造船者於是尋求快而高效率的船身,使得航行所燒的每一噸煤都能得到最充分的利用。
就在工業革命的那個年代、維多利亞時代的開端,有那麼一位有數學思想工程師約翰・史考特・羅素(圖 1),他開始要尋找一套通用的造船規律:一組能產生最小阻力的船身設計原理。他所完成的理論,被稱為「波浪線理論」(wave-line theory),主導了近半世紀的船舶設計世界。這一套理論不但引導了蒸汽船的設計,還加上得獎遊艇與破紀錄快速帆船。波浪線理論最終不再獲得青睞而被傅如德(Froude)更嚴格的理論所取代;這一段故事,在總是複雜的科學與技術的關係之中,是一課頗具啟發性的歷史。
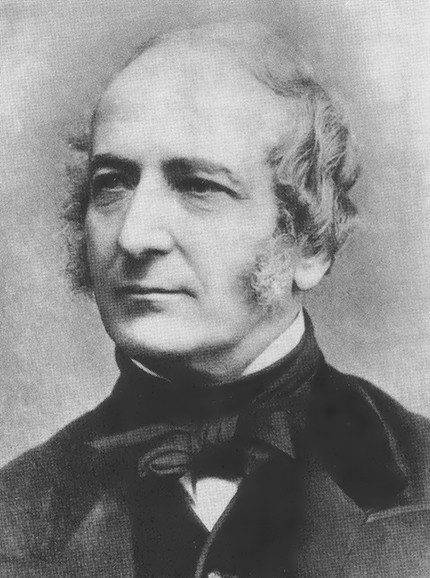
製造波浪,和決定吃水線?
作為一位廣受尊敬的造船者,羅素於 1821 年到 1825 年間在英國格拉斯哥大學(University of Glasgow)讀數學,隨後藉著製造蒸汽車與船用蒸汽引擎學會了機械貿易。他結合理論與實踐的訓練在當時英國幾乎無人能及[1]。
1835 年,他在尋求方法改善新開發的蒸汽船時開始發展波浪線理論。在當時,科學家們已經確認船舶航行所受的阻力主要來自流體壓力與摩擦。但是,羅素卻正確地主張產生波浪的是另一個重要因素。不過,他錯誤地把波浪的產生只歸因於船身的形狀;實際上,無論任何形狀,物體在水中移動時都會產生波浪。羅素力爭,因為傳統船身的吃水線都是鈍形的——這是指船身前端與水接觸的部分,也就是船頭兩側形狀是凸面的——所以當船必須持續把水推開才能前進時,就一定會產生波浪。羅素相信,一個有適當向內的凹面或窪陷的船頭,會將水向兩側排開而不會產生船頭波。

羅素在接著的 8 年裡努力的想要決定吃水線到底必須是甚麼形狀。英國科學促進協會(The British Association for the Advancement of Science,簡稱 BAAS),一個新成立的皇家學會(Royal Society)的競爭者,給了他 1132 英鎊——相當於今天的一百萬——讓他研究海浪的本質以及發展能減低波浪產生的船舶設計。這是該協會在那個時候所付出第二大筆的經費[2]。
大小從 3 英尺長的模型到 200 英尺長的遠洋航艦,羅素建造了並測試了超過 100 種船身。透過先前的實驗,他開發了精巧的技術:運用了懸吊自高支架的重物與滑輪系統來拖動船舶模型與運河船。在那些早期的實驗中,較高效率外型的船身自然跑得更快,但是阻力與速度之間的關係卻很難精確量化。羅素沒有單純的只去紀錄懸掛重物的落下時間,他使用了一種相對新穎的「彈簧動力計」直接量測航行受到的阻力,彈簧動力計還可以同時將得到的數據轉換為驅動船隻所需的馬力。在各項試驗之中,羅素甚至觀察到在運河中傳播而不會減速的奇怪「孤波」(solitary waves,後稱soliton)。孤波在光學與通訊裡扮演了重要的角色。
羅素在 1843 年向 BAAS 報告,在歷經幾千次實驗後,他發現了一種後來稱為波動線理論的新物理定律,「在這個理論裡,似乎每一種獨特形式與大小的船身都對應一個速度。」[3] 換句話說,羅素宣稱他發現了一個不論大小、任何船身設計都應該服贋的基本原理[4]。

什麼是波浪線幾何學?
羅素新定律的前提是,一艘船的船身形狀必須與它產生的波浪形狀一致。他假設有兩種形式的波浪與船所受的阻力有關:船行進時推開的水所產生、在船前方的「正弦移動波」(sinusoidal waves of translation),以及由風所驅動、回填至船通過後所空出來的空間所產生的「擺線船尾波」(cycloidal waves of replacement)。
羅素主要的研究聚焦在移動的波浪。他從實驗得到一個結論,就是正弦波的長度 L 必須遵守公式 L = 2πV2/g,其中 V 是船速、g 為重力加速度。羅素認為若要將阻力降到最小,船頭兩側的形狀就必須是長度為 L 的正弦。他從來沒有完全講清楚過他的論據,只是說這樣的對應關係能在平的水面產生最小的擾動——先別管水面其實沿垂直方向上下振動,而羅素的船身在水平面是正弦形的。所謂的波浪線船頭號稱會劈開迎面來的水,而不是將水向前推開。為了證實這個想法,羅素駕駛了一艘這麼設計的船穿過漂浮著小球的水面,他觀察到那些小球並沒有撞向船頭,而是單純的被向兩側推開[5]。
同樣地,羅素主張船尾的形狀應該做成擺線形以配合回填的水波。由於這種水波的長度是移動波長度的三分之二,所以船尾的長度應該是船頭的三分之二。而船舶的全長可以藉著在中間加進一段平行船身來調整。例如,一艘船以 10 節(每秒 17 英尺)速度行進時所產生的移動波長度是 53 英尺,所以設計一艘以這個速度航行的 100 英尺長的船應該有 53 英尺的正弦形船頭、12 英尺直的中段,以及 35 英尺的擺線形船尾(圖 2)。
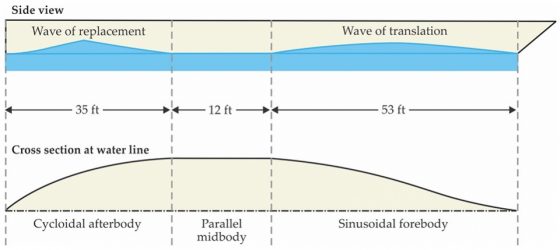
圖 2. 依照波浪線理論所訂出船身幾何形狀的三個關鍵元素,圖/物理雙月刊提供。
- 波浪線理論:船頭形狀必須是正弦的才能與船隻前沿所產生的移動波相匹配;船身後段/船尾必須是擺線形才能與尾隨的替代波相符;船身中段,由於假設沒有波浪,所以必須是直的而且與船身中線平行。船首與船尾的長度各自依據移動波與替代波的長度決定,而船身中段的長度則視船隻的全長來調整。
在這裡我們必須開始注意有甚麼是波浪線理論所沒有顧到的。波浪線理論並沒有提供一個方法來估計「興波阻力」(wave-making resistance,即船隻行進時,推動水面形成波浪所損耗能量對應的阻力);羅素單純的、錯誤的假設依據波浪線設計的船身的興波阻力為零。同時波浪線理論並無物理基礎;儘管羅素宣稱他做了好幾千次的實驗,但能用來闡明興波阻力機制的數據卻很少。
羅素堅持的正弦曲線以及擺線只能說是一種幾何描述性概念,而不太算是一個物理理論。最終,與羅素斷言相反,他的波浪線並無法為每一艘船隻提供保證成功的範本。船舶設計始終必須在速度、穩定性、強度與其他一堆因素之間尋求妥協。就波浪線來說,船身為了支撐其重量必需足夠吃水,往往就表示必須修正羅素原來想像的吃水線。
應用在蒸汽船的情況⋯⋯
羅素由 BAAS 贊助的研究成果發表之後,他的波動線船身設計理論就獲得蒸汽動力船造船者的擁護,而蒸汽動力船舶在那時候已經快速地在英吉利海峽、北海、愛爾蘭海等等貿易航線上取代風帆動力船舶了。在那些水域航行的貿易船隻必須相當快速的完成短程輸運;造船者看到比較尖的船身都認為那是產生速度的理想形狀,以致向內凹進去的吃水線設計在 1845 年之後大為流行。
雖然波浪線設計的汽船一般來說可以令那些船長們滿意,但僅僅使用波浪線公式並無法保證一艘船舶的成功。舉例來說,蘇格蘭的造船者詹姆士・納皮爾(James Napier)依據羅素理論所建造的幾艘在愛爾蘭海航行的汽船,就都通通不及格,這使得納皮爾的每一條船都大虧其錢。

雖然 1895 年時羅素已經是倫敦一位著名的造船者,但是他沒有標到建造皇家海軍第一艘裝甲戰艦「HMS 勇士號」(HMS Warrior)。不過他說服了海軍調查員保德溫・華克(Baldwin Walker)在建造新艦時採用波浪線概念。勇士號的首席造船技師埃撒克・瓦特斯(Isaac Watts)跟隨華克的決定,為戰艦製作了產生波浪線的向內凹陷的吃水線,但是船頭剩下的部分則仍舊依照傳統設計。而且瓦特斯也斷然拒絕了後來羅素要求分享一半勇士號設計功勞的嘗試。
羅素的確運用波浪線建造了他最著名的船——在 1859 年開始營運的「SS大東方號」(SS Great Eastern,圖3)。這船長 600 英尺、排水量 27,000 噸,在那個時代是最大的一艘船,準備從英國載客到澳大利亞。然而儘管是這麼大的船、還加上先進的船身外型,大東方號卻從來沒有去過南半球,她只數次橫渡大西洋,也沒有賺到利潤[6]。

儘管如此,大東方號的乘客之一,朱爾・凡爾納(Jules Verne)由於對大東方號的波浪線船身印象非常深刻,因此給了他靈感在他的著名小說《海底兩萬里》或譯《海底歷險記》(Twenty Thousand Leagues Under the Seas)裡寫了一段。在小說裡他這樣描述他的虛構潛水艇「鸚鵡螺號」(Nautilus):「有線條…足夠長而且她的船尾夠寬,能讓回填的水輕易的流出,而且讓潛艇的行進毫無障礙。」[7]。
如果用在風帆的情況?
雖然波浪線理論原來本是為了蒸汽動力船而發展的,卻在帆船上發揮了最大的功用,特別是在 1800 年中期到末期的快速帆船(clipper)和遊艇(yacht)上。快速帆船是被建造來快速輸運旅客和易腐爛貨物的;遊艇則是被造來贏得比賽中。這些船隻的設計與建造的每一方面都可以說是以快為本。
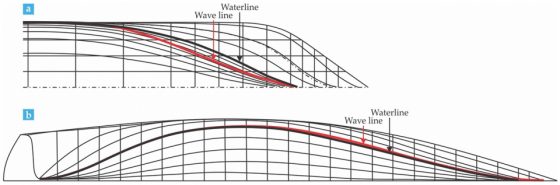
快速帆船最初是 1840 年代由一位任職於紐約史密斯與戴蒙(Smith and Dimon)造船廠的年青人約翰・葛瑞菲斯(John Griffiths)所發展出的。葛瑞菲斯想設計一款新型的船舶,以便在當時和中國之間快速擴大的茶葉貿易上撈到好處。他精通那時最新的船舶設計理論,也研讀了羅素各種波浪線理論的報告[8]。他最先設計的幾艘快速帆船:1845 年的「彩虹號」(Rainbow)和 1846 年的「海魅女號」(Sea Witch),就是受到羅素向內凹陷吃水線的啟發;這個設計使得往返美國-中國的航程幾乎縮短了近乎兩個月[9]。圖 4(a)所示為海魅女號船頭的波浪線。葛瑞菲斯設計的快速帆船是名列最快船隻之列:1849 年由海魅女號所創下的由紐約到香港的紀錄,一直到 2003 年才被打破!
葛瑞菲斯在快速帆船的成功,刺激了一股在紐約與波士頓採用向內凹陷吃水線造船的熱潮。快速帆船造船者羅伯・馬凱(Robert McKay)在一次造訪倫敦時簡潔的向羅素表示:「我有個秘密,就是我在建造我所有的船時都採用了波浪的原理。我最早是在大英協會(British Association)的出版品裡發現了波浪線的說明。[10]」
波浪線成了遊艇社群的一個更加招牌的設備。羅素幫英國鐵路工程師羅伯・史蒂芬森(Robert Stephenson)建造了一艘波浪線遊艇「泰坦尼亞號」(Titania),就是這一艘船讓史蒂文森得以加入那個貴氣十足的「皇家遊艇連」(Royal Yacht Squadron,簡稱RYS)。1851 年的時候,皇家遊艇連的會員邀請他們的同級對手「紐約遊艇俱樂部」(New York Yacht Club,簡稱 NYYC)的伙伴們到英格蘭懷特島的考斯(Cowes, the Isle of Wight)比賽「一百畿尼杯」(Hundred Guinea Cup/£100 Cup)遊艇賽——這是皇家遊艇連舉辦的比賽裡的最高殊榮。(譯者注:畿尼(Guinea)是英國幣值單位,一畿尼等於一英鎊,一百畿尼杯的獎盃價值一百畿尼,大約是今天的十萬英鎊。)

皇家遊艇連的好手們不知道,來自紐約由喬治・史悌爾(George Steers)所領導的隊伍,已經準備好了他們自己的波浪線遊艇來參賽。史悌爾曾經是葛瑞菲斯的造船伙伴,並而且向葛瑞菲司學會了波浪線理論;他完全遵照了波浪線理論建造了他的「美國號」(America)縱帆船(見圖 4(b))。
- 美國杯帆船賽原名「一百畿尼杯」(Hundred Guinea Cup),就因為美國號超凡的表現,後來改名為美國杯帆船賽。(改編自 C・G・戴維斯(C. G. Davis)所著《美國快速帆船海魅女號:1846 紐約製造》,1935 船舶製造廠出版(U.S. Clipper Ship Sea Witch: Built at New York, 1846, Ship Studio, 1935)與參考資料[8]。
在 1851 年的 8 月 22 日,美國號在懷特島的帆船大賽裡穩穩的擊敗了由 14 條船所組成的英國船隊。美國號的勝利造成了大轟動,數日之後倫敦日報(London Journal)登載了一幅漫畫,圖中維多利亞女王問道:「那一艘遊艇得到第二名?」她得到唯一的回答是:「啊,女王陛下,這個比賽是沒有第二名的。」一個星期之後,在另一場比賽裡,美國號對上了羅素自己的傑作泰坦尼亞號。再一次,美國號輕鬆獲勝[11]。羅素很有風度的承認對方的勝利並聲稱史悌爾對於波浪線的運用更勝他一籌。

波浪線贏得了國際的名聲而且在美國號大勝之後被廣為模仿[12]。1860 年的時候羅素被任命為「皇家船舶設計學院」(Royal Institution of Naval Architects)的校長。然而並非所有的帆船玩家都相信波浪線理論。一位在麻省理工學院訓練出的工程師,美國人那森諾・賀瑞修夫(Nathanael Herreshoff)明確的摒棄了波浪線以及所有其他所謂的「科學 理論」,在船身設計上只認同出自自身經驗的自家產品。他工程上的直覺被證明幾乎都是對的;自 1893 年到 1920 年,他設計並建造了連續五屆美國杯的衛冕者,這裡面包括了他 1903 年的傑作「信任號」(Reliance)。這幾條船沒有一艘有向內凹陷的吃水線特徵[13]。
對於許多研究船舶設計的科學家與工程師,賀瑞修夫的非凡演出其實也不是那麼令人驚訝。早在十多年前那些人之中有幾個就已經開始發掘波浪線理論的缺點,而並沒有花太久時間就看到那個理論出現了破綻。
波浪線的終結
在那些質疑波浪線理論的諸多科學家與工程師之中,有一位名叫威廉・藍金(William Rankine)。他自 1857 年開始,執行了一個為期十年的船舶阻力研究之後,得到了一個結論,就是船舶行進所遭遇的阻力最重要的來源是散流在整個船身周邊的「摩擦渦流」(frictional eddies);注意,摩擦渦流的作用不只是在船頭與船尾,而在整個船身。但是,藍金用來計算阻力的理論,雖然後來證明大都是對的,用在處理日常的造船工作時就嫌太複雜了[14]。
又有一位大名威廉・傅如德,曾經一起參與建造大東方號,亦熟悉羅素,也加入了船舶阻力的研究。1865 年的時候,他決定要比較一下羅素的尖型波浪線和另一種比較圓的,他說他的想法源自「水鳥的眼光」。他建造了兩組大小不同的模型船,一組是有波浪線的「渡鴉」(Raven),另一組船尾是鈍形的「天鵝」(Swan),然後把這兩種模型船拖在一艘小的工作船後面。實驗結果發現,在高速時天鵝表現出的阻力比渡鴉要小,傅如德也開始確信阻力可以依照比例隨著船隻大小予以預測。

1868 年,BAAS 委託了更多船舶阻力的研究案,而藍金和傅如德都參了一腳。在正式的報告裡,協會反對使用縮小版模型的行為來預測全尺寸船隻結果的作法。但是傅如德基於他所做天鵝與渡鴉的實驗結果,並不認同協會的看法。運用了得自皇家海軍(Royal Navy)的資金,傅如德在位於托基(Torquay)、他家附近建造了一個模型測試儲水池,並且在 1871 年開始實驗。經過十年研究,傅如德和他兒子羅伯(Robert)發展出了船舶阻力的比例定律[15]以老爸名字命名。
經過超過一個世紀的理論與實驗的證實之下,傅如德的定律架構裡說明了船舶所受的總阻力來自兩個可視為獨立的因素:
(一)壓力,就是在整個船體全長產生能量耗散波浪系統的壓力
(二)摩擦,就是由水施予船體表面的黏滯阻力。
波浪線理論只有船頭與船尾會產生波浪的前提,被一個更基本的理解所取代。這說明行船時產生的波浪,就是整個船體向其周圍的水所輸送的能量。
到了 1890 年代,蒸汽動力已經超過風帆成為商船推進的主要方式。船主們開始對增進煤及後來的油的效率投資更多的投資。在同一時期,全世界也在紛紛建造傅如德於托基做的實驗所用的縮小版模型測試儲水池,而模型測試的結果都確認了傅如德所建構的定律。船舶設計所涉及的科學很快也成為了在那些實驗設施裡工作的工程師與科學家的研究領域(圖5)。縮小版模型的實驗是相對容易與以及低成本,與傅如德的比例定律相結合後,模型測試對造船者以及海軍而言是有成本效益的方式,如此他們能發展有效率的船體形狀,同時降低燃料開支。

模型測試也逐漸顯露其他影響船隻速度與動力的因素,包括船身摩擦與流入螺旋槳的水流的形態。這些新考量質疑了所有幾何推導出的吃水線有效性。1906 年一篇刊登在暢銷的《工程學》期刊(Engineering)的論文認為:「早期船舶設計者絞盡腦汁要尋找一個『最小阻力』形狀的問題,除了在這個層次之外是仍未獲得解決的。這個層次就是科學的造船者已經知道,沒有哪『一種』船身的形狀能在『所有』的狀況之下都是最容易駕駛的;所謂『最小阻力』的船身形狀則是對應於不同的速率、長度以及其他船身狀物體的變數,有所不同。而約翰・史考特・羅素先生著名的《最小擾動與可能的最小阻力的波浪線形狀》只是演繹自…他所假設的公理[16]。」
該論文明言,這個主題「只能在測試水槽的輔助之下得到闡明」。確實,在 1893 年由美國造船技師大衛・泰勒(David Taylor)所著的、有影響力的著作《船舶的阻力與螺旋推進器》(Resistance of Ships and Screw Propulsion)中,幾乎完全只專注於模型測試結果,而對羅素的波浪線理論一個字都沒提到。
故事還沒完⋯⋯
雖然羅素的波浪線概念無法存留超過 19 世紀,但是 18 世紀明確的理想——最小阻力的幾何固體——活了下來。儘管被指出並無物理基礎,這種固體可能存在的想法仍繼續支配著一些甚至是 20 世紀的工程師。
在最有名的例子,1934 年美國航空工程師大衛・戴維斯(David Davis)申請了一種低阻力機翼設計專利,設計原理完全只基於擺線形狀的幾何考量。回顧羅素的論點——擺線形是最佳化船尾的形狀,戴維斯的專利宣稱他的「最有利機翼形狀」是「發展自一個公式,該公式是基於一個在流體中同時具有旋轉與平移運動的旋轉翼所產生的馬格努斯效應(Magnus effect)[17]」。

在這裡把馬格努斯效應扯進來其實是有點曖昧的,因為馬格努斯現象只與自旋的物體相干,而戴維斯的機翼並不旋轉。但是即便如此,戴維斯的機翼仍然受到了「統一飛機公司」(Consolidated Aircraft Corp)的注意,這家公司當時正在發展一種新式的長程轟炸機——就是後來的 B-24。當統一公司測試了戴維斯的機翼之後,發現流經機翼大部分表面的氣流都是非湍流的穩定流線,因此大幅降低了阻力。於是飛機公司就採用「老戴機翼」接續製造後來被視為大成功的 B-24。好幾年之後,大家才瞭解到這個低阻力背後的物理是所謂的「層流機翼」(laminar-flow airfoils),工程師們也就在那個時候才瞭解到戴維斯的擺線碰巧落在幾種層流機翼形狀的其中之一。看來戴維斯發表的機翼比較像是碰巧踩到狗屎般的好運而非出自刻意的設計[18]。
約翰・史考特・羅素與他在造船界半世紀長的主導似乎也頗為相似。然而,即使證據顯示他幾何構想的基礎,事實上只是建築在沙灘上的一段時間之後,他那個「最小阻力形狀」依然風姿不綽。部分魅力可能因為他的理論看來就是那麼簡單。但是另一個隱藏在波浪線和其他幾何導出形狀持久不墜背後的因素,應該是羅素作品的視覺美。這世界事實上沒有多少事物能比那些過去歲月中的快速帆船與賽艇優雅的船身還要漂亮。
- 本文的另一個更長的版本原本出版於《技術與文化》期刊(Technology and Culture)57, 414 (2016).
參考資料
- A. Lambert, Int. J. Hist. Eng. Technol. 81, 60 (2011).
- B. Marsden, in Technological Development Between Economy and Administration in Great Britain and Germany (19th/20th c.), E. V. Heyen, ed., Nomos (2008), p. 67.
- T. Wright, “Ship hydrodynamics 1710–1880,” PhD thesis, U. Manchester (1983), p. 98.
- G. S. Emmerson, John Scott Russell: A Great Victorian Engineer and Naval Architect, John Murray (1977).
- J. S. Russell, The Modern System of Naval Architecture, vols. 1–3, Day and Son (1864–65).
- D. Griffiths, A. Lambert, F. Walker, Brunel’s Ships, Chatham (1999).
- J. Verne, Twenty Thousand Leagues Under the Seas, W. Butcher, trans., Oxford U. Press (1998), p. 82.
- J. W. Griffiths, Treatise on Marine and Naval Architecture, or Theory and Practice Blended in Ship Building, 2nd ed., Pudny and Russell (1852).
- H. I. Chapelle, The Search for Speed Under Sail, 1700–1855, Bonanza Books (1967).
- The Literary Gazette and Journal of Archaeology, Science, and Art for the Year 1857, L. Reeve & Co (1857), p. 980.
- J. Rousmaniere, The Low Black Schooner: Yacht America, 1851–1945, Mystic Seaport Museum (1986).
- D. Kemp, Yacht Architecture—A Treatise on the Laws Which Govern the Resistance of Bodies Moving in Water; Propulsion by Steam and Sail; Yacht Designing; and Yacht Building, 3rd ed., Horace Cox (1897).
- C. Pastore, Temple to the Wind: The Story of America’s Greatest Naval Architect and His Masterpiece, “Reliance,” Lyons Press(2005).
- O. Darrigol, Worlds of Flow: A History of Hydrodynamics from the Bernoullis to Prandtl, Oxford U. Press (2005).
- D. K. Brown, The Way of the Ship in the Midst of the Sea: The Life and Work of William Froude, Periscope (2006).
- Engineering 81, 541 (1906).
- D. R. Davis, “Fluid foil,” US Patent 1,942,688 (9 January 1934).
- W. G. Vincenti, What Engineers Know and How They Know It: Analytical Studies from Aeronautical History, Johns Hopkins U. Press (1990).
- 本文感謝Physics Today (American Institute of Physics) 同意物理雙月刊進行中文翻譯並授權刊登。原文刊登並收錄於 Physics Today, July/2017 雜誌內(Physics Today 70, 7, 52 (2017); http://dx.doi.org/10.1063/PT.3.3627);原文作者:拉瑞・佛瑞若(Larrie Ferreiro)是一位船舶設計師與歷史學者。他任教於位在美國紐澤西州后伯肯(Hoboken, New Jersey)的史帝文理工學院(Stevens Institute of Technology)的系統與企業學院(School of Systems and Enterprises)及亞歷山大・波拉臘(Alexander Pollara)是一位就讀於史帝文理工學院航海安全中心(Maritime Security Center)的博士研究生 。中文譯稿:林中一教授,國立中興大學物理系。
- Physics Bimonthly (The Physics Society of Taiwan) appreciates that Physics Today (American Institute of Physics) authorizes Physics Bimonthly to translate and reprint in Mandarin. The article is contributed by Larrie Ferreiro and Alexander Pollara, and are published on Physics Today 70, 7, 52 (2017); http://dx.doi.org/10.1063/PT.3.3627). The article in Mandarin is translated by Prof. Chung-Yi Lin, working on Department of Physics, National Chung Hsing University.
本文摘自《物理雙月刊》39 卷 10 月號 ,更多文章請見物理雙月刊網站。


































