幾何學難題大突破！高維等角直線叢研究備受矚目

文／陳宏賓｜UniMath 主編、逢甲大學應用數學系助理教授

大約七十年前開始，有個和直線有關的離散幾何問題吸引了數學家的目光。你可能心底想，直線不就那樣，還能有什麼神祕嗎？嗯，有的。今天要和各位讀者分享的直線們有一些特別之處，那就是：

1. 全部都通過原點

2. 任意選取其中兩條直線，它們的夾角都是一樣的。

這樣一堆直線的集合就稱為「等角直線叢」（Equal-Angle Lines or Equiangular Lines）。

舉最簡單的例子（如下圖）來說，二維平面上正六邊形的 3 條對角線， 它們兩兩夾角都是 60度（或 120 度）。二維平面上，3 條線是最多的等角直線叢嗎？答案挺顯然的，Yes！

不過，三維的情況就沒有那麼容易想像。數學家已經證明三維空間最多就是 6 條，它們是正二十面體的十二個頂點所構成的 6 條對角線。這 6 條對角線恰巧形成等角直線叢，夾角是 arccos (1/√5)，大約是 63 度左右，請見下方影片。

超越想像極限的更高維度，就交給幾何學吧！

很自然地，人類的好奇心會驅使我們去探索未知的四維、五維空間，甚至去想像更高維度的情況究竟是如何呢？這就是離散幾何領域經典的等角直線叢問題。

不幸的是，高維度的情況無法用視覺化的方式呈現出來，某些程度阻礙了數學家透過空間感去想像其可能的分佈型態。不過，這並不足以令數學家退縮。

數感敏銳的讀者可能也已經隱約感覺到，形成最多的等角直線叢可能有以下兩項性質：

1. 高度對稱性結構

因為要找最多，直覺上有規律地適當安排在整個空間中應該比較有機會。這個特質除了滿足幾何學家對於美的追求、以及出於數學的純粹好奇心之外，這些具有對稱性且同時通過原點的直線們，恰好也會在一個球體表面穿插出一些兩兩距離相等的點，對應到應用數學領域和資訊領域裡一個重要的研究主題－－《球形碼 Spherical Codes》，讓這道古典離散幾何問題的重要性被凸顯出來。

2. 維度越高數量越多

直覺上我們會認為數量必定會隨著維度（嚴格地）增加；然而，事實卻並非如此。早在 1948 年數學家 Haantjes¹就證明了三維與四維最多的等角直線叢都是 6 條。換句話說，維度增加並不一定會增加等角直線叢的最大數量。

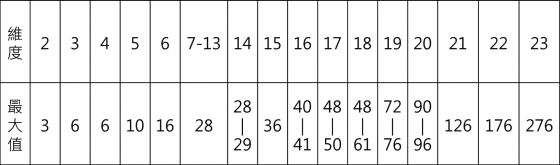
後來，范林（Van Lint）與西德爾（Seidel）²證明了五維到七維的結果。稍後，1973 年雷蒙斯（Lemmens）與西德爾³開創性地引入《線性規劃 Linear Programming》的手法，一口氣把戰線推進到 23 維以內，他們當年的結果整理如下表：

舉例來說，十四維已經有 28 條等角直線叢的構造，但不知道 29 條是不是可以達到，意即，數學證明 30 條以上是不可能的。所以，我們說十四維空間的等角直線叢數量最多介於 28 到 29 之間。

一個有趣的地方是，三維及四維都是最多 6 條，七維到十三維，都是最多 28 條。一般來說，維度越高越有更多機會造成更多條等角直線叢，但七到十三的維度變化不算少，最大值 28 卻聞風不動。專家們認為，這樣的現象在更高維度也會發生。

雷蒙斯與西德爾的文章裡，提到另一位數學家葛松（Gerzon）發現：等角直線叢的最大數量會受限於維度。他用《線性代數》裡大家一般熟悉的方法計算得出了一個通用的上界：

任意維度 n，等角直線叢的最大數量不超過 n(n+1)/2 。

例如 n = 7 和 23 的時候，最大值分別是 28 和 276，恰好達到這個上界。

年輕台灣博士與美國教授合作，突破四十年障礙

然而二十四維以上的進展，卻沉寂了將近 40 年之久。直到 2014 年，一位來自台灣的年輕數學博士俞韋亘（Wei-Hsuan Yu）和他的合作者巴格教授（也是他的博士班指導教授 Alexander Barg）⁴對這道難題有了新的進展。

俞韋亘目前於美國的密西根州立大學從事博士後研究工作。大學就讀新竹清華大學數學系的他，畢業後前往臺灣師範大學攻讀碩士，得到碩士班指導教授林延輯以及許多老師在數學研究上的啟發和鼓勵，後來前往美國馬里蘭大學繼續攻讀博士學位，邁入更高的學術殿堂。

解決問題需要有好的工具，2014 年這篇文章也不例外。他們首度引入運籌學領域的一種高端工具「半正定規劃」（Semidefinite Programming, 簡稱 SDP），藉此證明了二十三維到四十一維最多都是 276 條，印證了雷蒙斯與西德爾在 1973 年的想法。

一般來說，數學證明等號有兩個方向需要努力，也就是所謂上界（upper bound）和下界（lower bound）：
當維度 n 固定，構造出等角直線叢就會得到一個下界，內含直線的數量越多，得到的下界就越好。例如，在二十三維空間中，數學家從 276 個點的強正則圖（strongly regular graph）獲得啟發，找到構造 276 條直線的等角直線叢的方法，提供了 276 是二十三維等角直線叢最大數量的下界。

另外一個方向是，當維度 n 給定，用數學證明等角直線叢數量有其上限，不能再更高了。這就是所謂的上界。

俞博士和巴格教授⁴的突破就是利用 SDP 證明了二十四維到四十一維的上界恰好是 276 條。由於二十三維空間中已經有 276 條線的構造法，上下界碰在一起，於是就證明了從二十四維到四十一維，276 條等角直線叢就是最多的了。

證明等角直線叢的唯一性

坂內（E. Bannai）與斯隆（N. Sloane）在 1981 年⁵證明二十三維最大數量的 276 條等角直線叢具有唯一性。也就是說，這 276 條的長相只有一種。既然前面提到 23 維到 41 維也都是 276 條，一個很自然的問題就是，那 24 維到 41 維的 276 條有沒有其他異於二十三維的構造法呢？俞博士和另一合作者葛雷茲林 （A. Glazyrin ）在半年前得到了一個令人驚奇的結論⁶：

二十三維到四十一維的 276 條都是同一種構造。

同時，他們也證明了七維到十一維的 28 條，都是同一種構造。
至於十二維與十三維到底有沒有另外一種不等價的 28 條等角直線叢，目前仍是待解決的問題。

當角度不隨著維度變動

事實上，俞博士和葛雷茲林的論文中也探討了另一個觀點上的等角直線叢。

上述的最大數量規模可以達到 n² 的等級，不過達到這個數量規模的等角直線叢所夾的角度也會跟維度 n 有關（arccos (1/√n)）。因此，就很自然會去思考固定角度（與 n 無關）之下，在 n 維歐氏空間的等角直線叢的最大數量規模是否會小於 n² ？

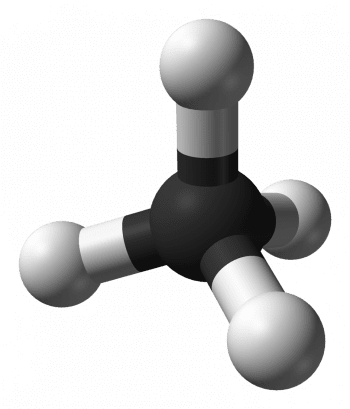
1973 年雷蒙斯和西德爾的論文裡，首度給出這個方向的結果；對於夾角 arccos(1/3)，等角直線叢的最大數量就是 2n-2 條。［補充：正四面體的四個頂點與中心點的連線那四條線是等角直線叢，夾角正是arccos(1/3)。學化學的人可以想像甲烷 CH4  的分子結構，四個氫原子鍵結碳的兩兩夾角也是arccos(1/3)］

又再隔 16 年，紐邁爾（A. Neumaier）證明：如果角度是 arccos (1/5)，則最大數量規模是 1.5 n 條，前提是維度 n 要足夠大（sufficiently large）。

對於其他角度，多年來人們知道的很少，數學家一直苦無對策突破。直到去年 2016 年六月，任職於瑞士理工大學的知名組合數學家蘇可達夫（Benny Sudakov，Noga Alon 的學生） 以及英國牛津大學數學系教授齊瓦胥（Peter Keevash，Sudakov 的學生）為首的研究團隊，開創性地引入「機率」、「圖論」、「拉姆西理論」、「代數」等多種數學分支的工具，摻在一起得到一個極具指標性的重量級突破。先說結論，他們的主要結果是：

對任意給定角度，當維數 n 足夠大，最多就是 2n-2 條等角直線叢；而且，能達到 2n-2 條的，只有當年雷蒙斯和西德爾所證明的 arccos(1/3) 這個角度。

蘇可達夫教授受訪時提到，自己是 2015 年聽卡內基美濃大學數學系的巴克（Boris Bukh）教授演講時，受到他的啟發才開始接觸這個問題。巴克在台上講述他在等角直線叢問題上的新進展時，提到自己用了一個「很醜陋」的方法來讓整個證明過得去，感覺就不是一個解決等角直線叢問題的好招式。

峰迴路轉，柳暗花明

蘇可達夫與齊瓦胥教授的研究團隊，依其利用數學分支工具的相關闡述如下：

圖論：點與邊之間關係的理論

最令人驚奇的創意在於蘇可達夫他們將等角直線叢這個幾何問題，轉換成圖論的語言，將空間中直線所對應的向量看成圖論裡的一個頂點。向量與向量的內積若是正的，給紅色邊；否則給藍色邊。這個轉換把高維空間中具有距離關係的幾何元素變成跟距離無關的圖論裡一個邊上塗兩種顏色的圖，提供數學家另一種完全不同的觀點來思考原始問題。

拉姆西理論

特別的是，經過轉換後，他們藉用圖論裡一個重要的研究主題－－拉姆西理論（ Ramsey Theory）來幫助規範紅色邊和藍色邊。拉姆西理論核心概念就是說，這樣塗滿兩種顏色的圖裡，總是會包含一定數量的頂點，彼此之間邊的顏色全部相同。打個比方，假設兩人之間關係只有「喜歡」和「不喜歡」兩種，在一個 50 人的團體裡，無論如何總是會找到 5 個人彼此互相喜歡或者彼此互相不喜歡。這麼一來，頂點的數量理論上就可以藉由拉姆西理論的概念來限制住。

矩陣

最後，他們將這樣子的一個圖再轉換成一種特別的矩陣來表示，矩陣中（i, j）位置填入的是第 i 個向量和第 j 個向量的內積值，然後就可以在上面玩一些矩陣的代數運算，也有相當豐富的矩陣理論可以派上用場。

研究等角直線叢問題多年的傑德瓦（Jonathan Jedwab）教授發表他對這項發現的看法時表示，我得知時的反應不是「懊悔為何自己沒有想到這個方法」，而是「老天爺啊！這群人擁有的數學工具也太多了吧。我認為他們最了不起的工作就是把這一卡車數學工具，一個接一個用在適當的地方。」

這個重要結果⁷引起國際上許多關注，國外知名媒體 Quanta Magazine 也寫了篇專題報導《 A New Path to Equal-Angle Lines 》，有興趣的讀者可以參考。

隔幾個月後，俞和他的合作者葛雷茲林教授⁶證明：當角度是 arccos (1/a)，在 n 維歐氏空間中，等角直線叢的數量上界約是 0.66a² n。這是首度對於任意維數與任意角度的等角直線叢給出上界的結果。蘇可達夫團隊發表的論文裡的一般上界雖然只有 1.92 n，但前提是 n 必須要足夠大才會正確。至於 n 要多大？目前仍是未知！

俞與其合作者在等角直線叢發展出來的這套數學方法，同時也可以用來處理離散幾何領域「最大球面二距離集」問題。什麼是二距離集（two-distance sets） 呢？空間中的一些點，如果所有的點兩兩之間彼此的距離收集起來只有兩個不同值，那麼這些點我們就稱為二距離集。將這些點限制在單位球（unit ball）上，稱之為球面二距離集 （spherical two-distance sets）。「最大球面二距離集問題」即是在尋找最大的球面二距離集的相關研究。

俞韋亘受訪時說：「我近期最開心的工作，就是利用這套方法改進了無窮多維的等角直線叢上界，並用之解決了拓樸學家 Oleg Musin 教授一個關於球面二距離集的重要猜想 Musin Conjecture」。

還好奇到底哪裡找來這麼多數學問題給數學家研究嗎？解決一個問題的同時，就會產生新的問題。這就是數學。

後記：今年暑假俞韋亘博士將會短暫回到台灣，到位於台大公館校區的國家理論科學研究中心（簡稱理論中心）及中央研究院數學研究所進行學術交流，排定於 7/24 及 25 兩日演講等角直線叢與最大球面二距離集的相關問題，歡迎報名參加。上述演講由理論中心支持補助。演講資訊請參考理論中心官網。

資料來源

• 《A New Path to Equal-Angle Lines》，Quanta Magazine.

參考文獻

1. J. Haantjes, Equilateral point-sets in elliptic two and three-dimensional spaces, Nieuw Arch. Wisk., 22 (1948) 355-362.
2. J. H. van Lint and J.J. Seidel, Equilateral point sets in elliptic geometry Proc. Nedert. Akad. Wetensh. Series 69 (1966), 335–348.
3. P. W. H. Lemmens and J. J. Seidel, Equiangular lines, Journal of Algebra 24 (1973), 494–512.
4. A. Barg, W-H. Yu, New bounds for equiangular lines. Discrete Geometry and Algebraic Combinatorics, A. Barg and O. Musin, Editors, AMS Series: Contemporary Mathematics, vol. 625, 2014, 111-121.
5. E. Bannai and N. J.A. Sloane, Uniqueness of Certain spherical codes, Can. J. Math., Vol. XXXIII, No. 2, 1981, pp. 437-449.
6. A. Glazyrin, W.-H. Yu, Upper bounds for s-distance sets and equiangular lines, Arxiv: 1611.09479.
7. I. Balla, F. Dr¨axler, P. Keevash, B. Sudakov, Equiangular Lines and Spherical Codes in Euclidean Space. Arxiv: 1606.06620.

本文轉載自 UniMath，《[離散幾何學突破]組合學大師與新秀分別出招，等角直線叢研究大躍進》

作者簡介：陳宏賓 － UniMath 主編、逢甲大學應用數學系助理教授。
數學既深且廣，我懂得不多，最喜愛組合數學相關領域，主要研究興趣是群試理論、圖論及最優化分解。2013 年出版「Partitions: Optimality and Clustering, Volume II: Multi-Parameter」一書（與 Uriel Rothblum 和 Frank K. Hwang 教授合著）。對於數學和教育有強烈的熱忱和使命感，積極創立 UniMath 電子數學媒體，致力於推廣數學文化。

關於 UniMath：UniMath (You Need Math)是一個 Online 數學媒體，我們的目的是成為一個線上平台，發表數學相關的科普文章及影音，使數學用更柔軟的姿態走入群眾，提升數學素養。歡迎加入 Facebook 粉絲團知道第一手訊息！