- 作者:林澤民(奧斯汀德州大學政府系)、陳怡璇(奧斯汀德州大學新聞學院)
To Be or Not to Be?媒體在臉書上的抉擇
近年來,臉書成為讀者看新聞的主要管道。媒體在臉書上分享文章鏈結,從臉書上引導流量回到自己的新聞網站。尤其是當自己網站上流量不多的時候,小編們就趕快在粉絲專頁上分享文章,很快就可以把臉書上的流量導回自家網站。臉書也非省油的燈,不願媒體把自己的用戶導離開臉書,仗勢自己廣大的用戶群,推出即時文章(instant article),與之合作的媒體,把內容免費提供在臉書上以換取跟臉書的廣告拆帳與珍貴的用戶資料(透過臉書上的用戶資料,就能夠更精準地賣廣告),如此,臉書用戶看新聞,不需再離開臉書,而臉書擁有這些免費內容,不但吸引更多用戶,也把每個用戶成功地留在自己的平台上。
媒體紛紛加入即時文章引發不少質疑與憂心:當新聞媒體把自己最珍貴的資產──內容──免費貢獻在臉書上, 等於棄守自家的網站流量,把自己的讀者帶到臉書後,恐怕以後也帶不走了,因為讀者已經習慣在臉書上看新聞。當媒體的經濟命脈依附在臉書之上,以後臉書更改規則,媒體也不得不從。縱使擔憂聲浪不小,所有媒體仍舊前仆後繼的加入即時文章。這種明知行動有後果卻不計後果行動的狀況,可用賽局理論中的多人囚徒困局來解釋。本文先說明賽局理論的概念、雙人囚徒困局的成立條件、多人囚徒困局形成的條件、最後用多人囚徒困局理論來看媒體所面臨的困境。
賽局理論及囚徒困局
賽局理論的基本概念:
.優勝策略:不論其他參賽者採取何種策略對自己都是比較有利的策略。
.納許均衡:沒有參賽者願意「單方面」改變策略的策略組合。
.伯瑞多最佳結果:參賽者無法「同時」改進的賽局結果。
.困局:納許均衡不是伯瑞多最佳結果的局面。
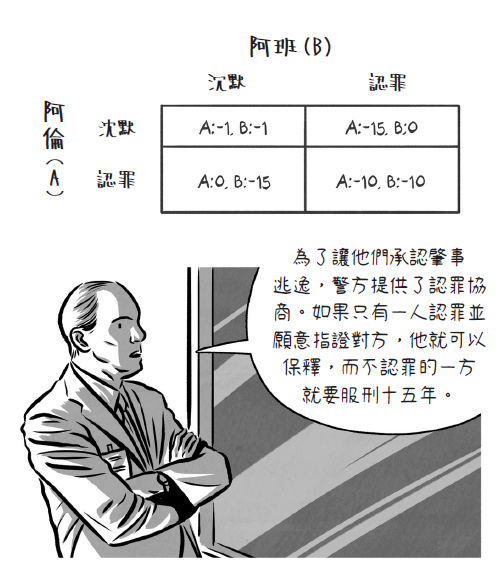
二人囚徒困局的收益可用下列矩陣呈現:
- A、B:參賽者
- C、D:策略;C = Cooperate(合作),D = Defect(不合作或背叛)
- TA, RA, PA, SA:參賽者 A 在表中各種策略組合下的收益
- TB, RB, PB, SB:參賽者 B 在表中各種策略組合下的收益
- T = Tempation(誘惑),R = Reward(獎賞), P = Punishment(懲罰),S = Sucker’s Payoff(傻瓜收益)
當 A、B 都只為自己的利益著想,而且彼此無法達成可信承諾時,如果 T > R > P > S 對 A、B 都成立,則 D 是兩位參賽者的優勝策略,相互背叛是納許均衡,可是這個唯一的納許均衡並不是一個伯瑞多最佳結果,因此賽局是囚徒困局。
- 關於囚徒困局的理論和應用,請參考林澤民在【泛科學】的《囚徒困局系列》特輯
公有地的悲劇
討論媒體在臉書上的策略互動之前,讓我們先看看下面這個雙人賽局:
在這個賽局中,參賽者從公有資源獲得屬於自己的利益。如果他們合作——有節制、不過度使用公有資源——他們都得到利益 b。如果一個參賽者合作、另一個參賽者不合作——過度使用公有資源——不合作者可以獲得較大的利益 B,可是同時卻造成了 -e 的外部效應,例如使得資源之永續性減弱,而這外部效應兩人都得承擔。當兩個參賽者都不合作時,兩人都都得到較大利益 B,但同時也得承擔兩份外部效應(-2e)。
這裡很容易證明當 2e > B-b > e 時,T > R > P > S 對 A、B 都成立,因此在這個條件下,抽取公有資源的問題是一個囚徒困局。這個困局就是雙人版的所謂「公有地的悲劇」。當個人過度使用公有資源時,雖然可以比有節制地使用能為自己帶來更多利益,可是當大家都這樣做時,集體造成的總外部效應(資源無法永續)卻會使得大家相互背叛的狀態比大家相互合作的狀態更糟糕。這個情況宛如一個「性格決定命運」的希臘悲劇:自私的「理性」驅使著每一個人無情地走向互相背叛的納許均衡,他們明知這個狀態不是伯瑞多最佳結果,卻有如陷於泥淖難以自拔,無法憑一己之力來改變資源毀滅的整體命運。

我們認為這正是新聞媒體在臉書上所面臨的狀態。
在這裡,公共資源是臉書上的讀者群。媒體之間的合作策略是有節制地使用臉書——只提供鏈結而不提供內容。當媒體合作時,他們得到較小的利益 b 而不必擔心後果。當媒體背叛——在臉書上提供新聞內容——他們可以得到較大的利益 B(雖然損失自家網站的讀者,但在臉書上吸引到的讀者大於損失),可是同時卻造成了臉書之外整個新聞媒體讀者的流失。這個代價 -e 是個外部效應,因為它不但影響到分享新聞內容的媒體自己,也因為助長讀者對臉書的依賴而影響到整個產業。因為當一家媒體提供新聞內容給臉書之後,臉書使用者不需要離開臉書就可以看到新聞,這些使用者也不再造訪其他媒體的網站,而影響其他媒體網站的讀者數量。為了避免被提供內容給臉書的媒體影響到,各家媒體因此跟進,長期以降,各家媒體必須依賴臉書觸及讀者,傷害整體產業的經濟自主。
湯瑪斯.謝林的多人囚徒困局
要把上面的雙人賽局擴大成多人賽局,我們必須要先了解多人囚徒困局的定義。這是 2005 年諾貝爾經濟學獎得主湯瑪斯.謝林(Thomas Schelling)的偉大貢獻之一。以下的討論見於他的 《微觀動機與宏觀行為》一書。
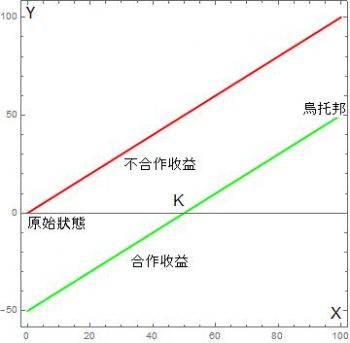
上圖中,縱軸(Y)代表收益,橫軸(X)代表除了自己以外合作的人數,紅線代表不合作的收益,綠線代表合作的收益。這圖有四項特徵:
1. 每個參賽者均有兩個策略選擇:合作或背叛(不合作)。
2. 不論其他有多少人合作,對自己而言,不合作的收益總要比合作的收益來得高。這也就是說,不論其他人合作或不合作,不合作是自己的優勝策略,而大家相互背叛的「原始狀態」是納許均衡。
3. 紅線跟綠線均隨著合作人數的增加而升高,也就是說不論自己合作與否,「傻瓜」越多越好。
4. 綠線隨著合作人數增加而升高時會超過原始狀態,如 K 點所示。當傻瓜的總人數(K+1)多到這個程度時,他們可以說是一個「可行的聯盟」(viable coalition)。這時雖然不合作還是比合作的收益要來得高,但傻瓜們至少可以說他們的收益比相互背叛時好。這個條件成立的充分且必要條件是所有參賽者都合作時的收益高於原始狀態的收益。我們把所有參賽者都合作的狀態稱為「烏托邦」。烏托邦的可行性代表原始狀態的納許均衡不是伯瑞多最佳結果。
因為上述條件蘊含了唯一的納許均衡不是伯瑞多最佳結果,湯瑪斯.謝林把符合以上特徵的人際競合關係界定為多人囚徒困局。以下我們檢驗多家媒體在臉書的策略互動為公有地悲劇型態多人囚徒困局的條件。
媒體在臉書之公有地的悲劇
我們假設市場上共有 n 家媒體。因為每家媒體在決定自己的策略時,必須考量自己以外有幾家媒體會合作(只提供鏈結、不提供免費內容給臉書),我們假設這個數目為 x。
根據以上的假設,每家媒體合作或不合作的收益作為 x 的函數可以分別定出如下:
.不合作的收益為:u(D|x) = B-(n-x)e = B-ne+xe
.合作的收益為:u(C|x) = b-(n-(x+1))e = b-(n-1)e+xe
由此我們可以演繹出幾個有用的結果:
.在原始狀態,也就是大家都不合作時,媒體的收益為:u(D|0) = B-ne
.在烏托邦狀態,也就是大家都合作時,媒體的收益為:u(C|n-1) = b
.當 x 固定時,不合作與合作的收益差別為:u(D|x)-u(C|x) = B-b-e
我們現在可以根據謝林的多人囚徒困局四條件來分析這個賽局了:
1. 每家媒體有兩種策略:合作(不提供免費內容給臉書)或不合作(提供免費內容給臉書)
2. 因為 u(D|x)-u(C|x) = B-b-e,我們可以推論當 B-b > e 時,不論 x 是多少,也就是不論自己以外有幾家媒體合作,不合作會比合作為媒體帶來更大的收益。B-b > e 是不合作為優勝策略的條件。
3. 因為 u(D|x) 與 u(C|x) 的式子中 x 的係數 e 為正值,也就是 u(D|x) 與 u(C|x) 均與 x 成正比,當越多人合作時,媒體不論合作或不合作,其收益都會越高。
4. 如果 u(C|n-1) = b 大於 u(D|0) = B-ne,也就是當 b-(B-ne) > 0 或 ne > B-b 時,烏托邦狀態的收益高於原始狀態的收益。因此,ne > B-b 是原始狀態不是伯瑞多最佳結果的充分且必要條件。
綜合以上四點,我們可以結論:當 ne > B-b > e 時,不合作是每個個別媒體的優勝策略,大家都不合作是納許均衡,可是這是一個不是伯瑞多最佳結果的納許均衡。根據謝林的定義,在這個條件下,媒體的臉書困局是一個多人囚徒困局。他們的處境正是一個公有地的悲劇。
ne > B-b > e 這個條件意指提供免費內容給臉書所帶來的額外收益(B-b)要大於媒體新聞網站讀者人數下降的代價(e),可是它同時必須小於整個產業都提供內容給臉書所造成的總代價(ne)。如果收益小於或等於個別代價(B-b≤e),提供內容不划算,合作才是優勝策略;如果收益大於或等於總代價(B-b≥ne),原始狀態比烏托邦還好,是伯瑞多最佳結果,沒有困局可言;這兩種情況都不是囚徒困局。請注意:當 n = 2 時, ne > B-b > e 這個條件正與上面所舉的雙人囚徒困局的條件相符合。
下面進一步申論 ne > B-b > e 這個條件。
第一, 提供免費內容給臉書帶來的的額外利益超過個別媒體之外部效應:B-b > e
華盛頓郵報曾經表示,提供免費內容給臉書,是預期透過臉書,他們可以觸及更多讀者,而有機會把臉書上的使用者變成自己的讀者(Marshall, 2015)。可見,新聞媒體自己的網站所能吸引到的讀者數量已遠遠不及臉書上的使用者。只要文章一放在臉書上,就可以吸引比在自己網站更多讀者。因此,能夠立刻吸引到讀者的這個利益,與長期依附臉書會失去自己網站上讀者的代價對照考量,當然先選擇解決目前的困境,長遠的負面影響,也是以後再說。
第二,提供免費內容給臉書帶來的的額外利益低於集體總外部效應:ne > B-b
提供免費內容給臉書得到的是即時利益然而付出的卻是整體新聞業的經濟自主與新聞自主,這也是許多專家大聲疾呼,與臉書打交道千萬三思(Riedmann, 2015)。 吸引媒體提供免費內容如同木馬屠城:臉書先以非常優厚的條件(廣告拆帳與用戶資料)交換媒體的內容。從此讀者透過臉書看新聞,就不再造訪媒體自己的網站,所以提供免費內容給臉書,等於放棄自己網站上的流量。當媒體的經濟命脈建立在另一間大企業上,等同於交出自己的經濟自主權。媒體在臉書上吸引到的讀者仍舊屬於臉書的用戶,等於失去臉書,媒體就失去讀者。以後媒體的廣告收入與讀者資料,都由臉書掌握。臉書一旦更改運算法,各家媒體就要立刻改變新聞生產策略以迎合運算法,才能確保自己的內容能夠推播到更多讀者面前。臉書成為真正的守門人,由運算法決定誰可以看到什麼內容。依賴臉書,一則失去的是經濟自主,二則失去的是新聞自主。
這場賽局中,新聞媒體用自己最珍貴的資產──新聞內容──交換短期的讀者數量,長期來看,犧牲的卻是經濟自主與新聞自主。這也是為什麼此舉引起一片憂心,認為與臉書的這場交易如同一場鴻門宴。媒體或許心裡都有數,拿免費新聞吸引讀者是飲鴆止渴,只是死得慢,但提供免費內容給臉書,就有立即經濟收益,也難再考慮之後的隱憂,因為隱憂畢竟只是「隱憂」,現在不加入,失去的則是眼前的廣告收入。在這樣的狀況下,即使知道或許不該加入,卻也不得不交出自己最珍貴的資產,冒著自主性的風險,交換即時利益。然而在這場媒體間的集體困局中,臉書成為最大贏家,獲取更多免費內容,吸引更多用戶,等於吸收他人的資產(內容與讀者),壯大自己的王國。
紀念湯瑪斯.謝林

2005 年諾貝爾經濟學獎得主湯瑪斯.謝林(Thomas Schelling, 1921-2016)在 2016 年 12 月過世了。謝林在學術上的重要成就是把賽局理論的關注從零和賽局導向非零和賽局,從合作賽局導向非合作賽局,並把行為概念結合純數學而讓賽局理論能夠廣泛地應用於社會領域和日常生活之中。雖然他最為人所知的是《衝突的策略》一書,特別是其中所論述「可信的承諾」(credible commitment)這一概念在冷戰年代國際關係上所發揮的影響,我卻偏愛他另一本著作:《微觀動機與宏觀行為》。我在學生時代讀他這本書,深深地為其中一個先驅性的「代理人基模型」(agent-based model)──個別居民無害的選擇如何在與鄰居互動的過程中造成社區種族隔離的均衡狀態──所吸引。及到大學教書,第一年即採用這本書開授「人類理性行為」的課程。
二十幾年來,我每次向學生介紹書中「多人囚徒困局」(multi-person prisoner’s dilemma)的理論時,仍然深深為謝林的智慧所激勵。這不只是因為模型本身既優雅又含意深遠,也是因為它所能洞燭的行為困境,從政治、經濟、社會、乃至於國際關係、人際關係幾乎無所不包。有不少人尊謝林為當前顯學行為經濟學之父,我深為同意。本文用一種特殊形態的多人囚徒困局──「公有地的悲劇」(the tragedy of the commons)──來詮釋新聞媒體在臉書上競合的困境。寫作中想到謝林對學術界、對我個人的深遠影響,不禁感懷不已。
原刊載於Tse-min Lin 的部落格
參考書目:
- Marshall, J. (2015). Facebook mulls Ad changes for Instant Articles after publisher pushback. The Wall Street Journal. Retrieved November 27, 2015
- Riedmann, G. (2015). 5 reasons publishers should think twice about Facebook’s tempting offer. INMA. Retrieved December 3, 2015
- Schelling, Thomas C. (1960), The Strategy of Conflict, Harvard University Press. (中譯本:《入世賽局:衝突的策略》,湯瑪斯‧謝林著,張華譯,達人館出版社)
- Schelling, Thomas C. (1978), Micromotives and Macrobehavior, W. W. Norton.(中譯本:《微觀動機與宏觀行為》,湯瑪斯‧謝林著,高一中譯,臉譜出版社)