交換禮物抽法其實不公平？數學家教你絕不失敗的玩法

一年一度的聖誕節又快要到了，大家最期待或是最感困擾的事情之一應該就是交換禮物吧！如果是和朋友交換的話，自然是邁向新年之前最期待的事；但如果是在職場上和不熟的同事交換，腦中小劇場演了好多究竟要如何拿捏分寸才好真是十分困擾。

交換禮物是件既期待又害怕傷害的活動！圖／By Kelvin Kay, CC BY-SA 3.0, wikimedia commons

西方基督教的聖誕節傳統之一是秘密聖誕老人（Secret Santa），大家在匿名的情況下彼此不知道誰送誰什麼禮物，只知道自己要送哪一個人禮物，所以這活動叫做秘密聖誕老人；但在台灣的交換禮物派對，普遍來說在大庭廣眾之下送禮物、拆禮物、惡搞禮物才是活動的高潮，很少玩匿名的秘密聖誕老人。

今（2016）年 11 月英國數學家漢娜．弗萊（Hannah Fry）以及湯瑪士．伊凡斯（Thomas Oléron Evans）出了一本新書，叫做《聖誕老人的存在是不爭的事實》（The Indisputable Existence of Santa Claus）[1]，裡頭就有一章專門介紹交換禮物的數學。無論匿名與否，交換禮物其實有很多種抽法，不同的抽法會影響誰是你／妳的送禮對象。

接下來我們就跟著英國數學家的腳步來看看交換禮物的數學吧！

聖誕老人的存在是不爭的事實。圖／@ Amazon

第一種是最常見的方法，一個一個輪流抽，如果抽到自己的號碼再把紙條丟回去，算是一種基本常識，總不會有人希望抽到自己的禮物吧。可是如果最後一個人抽到自己的號碼呢？這時候沒有固定的解法，有可能隨便和一個人換禮物，但這種解法除了尷尬之外，同時失去交換禮物的意義；或者是大家全部重抽一次，不過這除了麻煩之外也難保下一次不會再發生同樣的事情，不論哪一種都有點棘手。

對數學家而言，交換禮物只不過是一種排列組合。來看看如果只有三個人交換禮物，抽禮物的順序是如何影響誰送誰的機率！

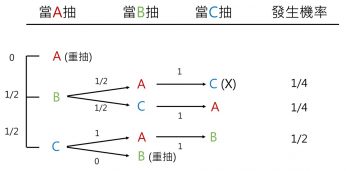
現在有 A、B、C 三個人玩交換禮物，我們將所有抽籤的可能性整理成以下的圖表，抽到誰就表示要送禮物給誰。當 A 第一個抽，有可能抽到 A、B、C 其中一個，將 A 抽到自己的狀態扣除，以 X 表示，因此這條路線的機率是 0，而這時 A 抽中 B 或 C 的機率各是 1/2。接下來輪到 B 準備抽籤，如果剛剛是 A 抽中了B，那 B 可以抽 A 或是 C 機率各是 1/2，不過這時如果 B 抽到 A 的話，那 C 就只能自己和自己交換禮物，因此也等於交換失敗（X）；如果 B 抽到 C，那 C 就只剩下 A 可以抽，機率是 1。A 送 B、B 送 C、C 送 A的機率是 1/2 × 1/2 × 1 = 1/4。

那如果 A 一開始抽到 C 呢，換 B 抽的時候如果抽到自己就會丟回去重抽（X），所以只剩 A 可抽，機率為 1，換 C 抽的時候也只剩下 B 可抽。因此 A 送 C、B 送 A、C 送 B的機率是 1/2 × 1 × 1 = 1/2。

從上圖發現兩條路線中送禮對象的機率竟然不同，C 送 B 的機率竟然是 C 送 A 機率的 2 倍。就算不是 A 先抽也一樣會發生同樣的問題。最常見的交換禮物抽法，實際上會影響送禮對象的機率，很顯然這種抽法並不公平，即使人數較多也是如此。

那如果換個方法大家一起抽呢？也就是一個一個抽卻不當場打開紙條，大家一起打開這樣就不會受到丟回去的紙條影響，可以把這樣的抽法視為一種排列組合。但如果是這種玩法的話，愈多人玩交換禮物，就會有愈高的機率有人抽到自己的禮物，一般來說大約是高達 63 %的機率有人會抽到自己的禮物[2]，即使參與人數不同也大約是這個數字。應該沒人會有耐心這樣慢慢玩，只好捨棄第二種大家一起抽的方法。

抽一次就成功的交換禮物方法

從以上的兩種方法可以發現，玩交換禮物需要的是一種不會抽到自己名字的排列組合，在數學上稱為錯位排序（derangement）。

英國數學家在書中提出了第三種方法能夠符合錯位排序，又有以下的優點：程序透明（大家自己動手抽不是用電腦）、公平（每個人送給其他人的機率相等）、有效率（一次搞定，絕不會再抽第二次）、秘密（包括主持人在內，沒人知道誰是誰的秘密聖誕老人，雖然這優點在台灣似乎不被認為是優點）。

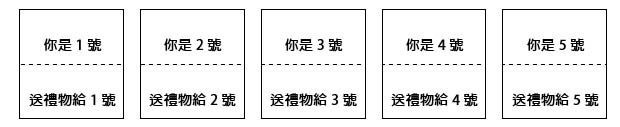
方法像是下面的圖在紙的上方寫上自己的號碼 「你是 2 號」，下方則是寫上「送禮物給 2 號」，大家分別寫上屬於自己號碼如下：

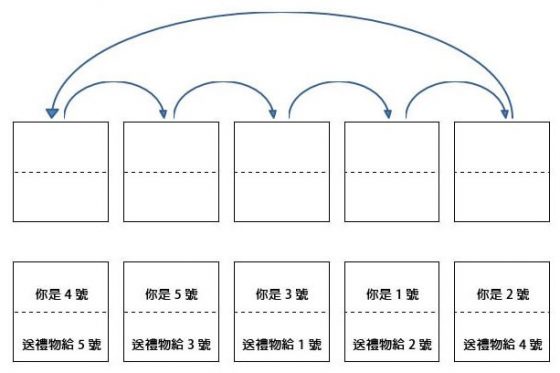
再來搜集所有的紙條，將它們翻到背面並將順序打亂，重新排列成一個直線。接著關鍵步驟來了，沿著中間的虛線剪開紙條。接著把紙張上半部（你是 O 號）向右移一個位置，最右邊的紙條則是移到最左邊，如此一來就完成了交換禮物的配對。紙條上面的號碼代表聖誕老人是幾號，下面的則是收禮物的人。最後大家在另外一張紙上填入自己的號碼和名字，如此一來就知道該把禮物送給誰了。

第三種方法中不會有人抽到自己的號碼沒拿到禮物，而且只要抽一次就能完成，是一種簡單而有效的方法，唯一的小缺點是不會有兩個人互相送禮。英國數學家認為這未必是缺點反而是 Z > B 呢，看來這樣的認知也是文化上的差異。如果不想在聖誕節也感受到職場上表面河蟹的氣氛，可以考慮用第三種方法加上匿名。

話說第一種方法也不是完全沒用，可以用在想要送給心儀的對象卻又不敢直接送，人少少的交換禮物派對之下，不用默默祈禱也不一定要和主持人串通好，透過數學就能知道，如何讓你／妳的禮物送到對方手上的機率增加。

很數學的聖誕節

除了秘密聖誕老人之外，英國數學家還在書中介紹了許多關於聖誕節的數學，像是裝飾聖誕樹的數學、怎樣送禮效果才會好、控制烤雞溫度的方程式、分析與模仿英國女王的聖誕夜談話、聖誕老人在旅途中是胖了還是瘦了？不得不說英國數學家真的相當有創意，讓大家知道數學除了實用之外也很有趣。

而且兩位作者最近在推特上（@FryRsquared 和 @Mathistopheles）舉行聖誕節的「每日數學小活動」（The Indisputable Santa Mathematical Advent Calendar），從 12 月初開始到現在已經累積了許多數學謎題。第一天的活動是開放讀者投稿數學聖誕裝飾，最佳的五名可以獲得他們的新書。最後選出了六名，得獎作品在此網址。有興趣的讀者可以用#Christmaths 這個 hashtag 搜尋，會有更多有趣的貼文和圖片。

參考資料：

1. Fry, H., Evans, T.O., The Indisputable Existence of Santa Claus, Doubleday, UK, 2016
2. 黃俊瑋，交換禮物中的機率問題（The probability of exchanging gifts），2014