兒時的電腦遊戲「大富翁」裡,有個道具叫「均富卡」,其功能是讓所有玩家手上的現金平分。雖然說炒地皮才是這個遊戲的致勝之道,但均富卡仍是出門在外,居家旅行,爾虞我詐的必備良卡。
面對真實世界中「收入不均」的問題,有時也希望拿張「均富卡」來解決,然而均富卡是虛幻的,要改善這種狀況,必須有良好的法令及稅制。不過在研究什麼是好的法規前,也許我們要搞清楚一個更根本的問題:怎樣的收入分配才算公平?
這個問題不好回答,但可確定「均富卡」式的齊頭平等並非好答案。就像去應徵工作時,不會期望當保全和當CEO會有同樣的收入。而且回答這個問題很容易得罪人,所以當政治人物被問到「怎樣的收入分配才是公平?」時,最佳的回覆或許是「我們需要社會有一定的共識,而且要有完整的配套及過渡,用謹慎的態度面對這個問題。」

如果你對政治式的回答不滿意,不妨看看哥倫比亞大學化工系的Venkatasubramanian教授和工業工程系的Sethuraman教授如何用「統計力學」的方法來尋求答案。
(謎之音:Venkatasubramanian教授的姓也太長了吧!)
看到「統計」二字,首先聯想到馬克·吐溫所說的:「謊言,該死的謊言及統計數字」。不過「統計力學」其實和「統計學」是完全不同的概念。統計力學是藉由配分函數(Partition function),分析一個有大量組成成分的系統,將微觀物理狀態與宏觀物理量統計規律連結起來的科學─聽起來有點難懂啊!好在中文的世界博大精深,可用成語解釋之,統計力學就是一個「觀微知著」的科學。
比方說,觀察一枚銅板,知道它擲出後有一半的機率是正面,一半機率是反面,就可以推論出丟二枚銅板時,出現兩個正面或兩個反面的機率各是1/4,而出現一正一反的機率是1/2。
此問題由統計力學的角度觀察,會牽涉到一個較為抽象的概念,謂之「熵」。「熵」的大小取決於系統所包含的狀態數,一個封閉系統的「熵」通常只增不減,當「熵」達到最大值時,系統即處於統計上最可能出現的狀態,或稱之為平衡態。以二枚銅板的系統為例,一正一反的狀態數為2 (正反、反正),二個正面或二個反面的狀態數各為1,故一正一反是此系統最可能出現的情況。「熵」的概念在丟銅板的問題中顯得有些多餘,但面對更繁雜的系統時,「熵」是不可或缺的思考工具。
統計力學發展之初,乃用於解釋熱力學中關於氣體分子運動的問題。科學家用類似丟銅板的概念加上複雜許多的數學,可以從一個氣體粒子該處於何種能量態的角度出發,推導出在平衡態時,一團理想氣體在給定溫度下各個分子的速率分布狀況,稱為「波茲曼分布」。
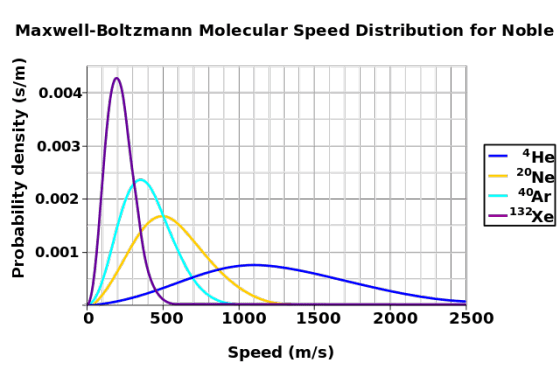
Venkatasubramanian等人建立的自由市場模型,則是推導出資方總薪水預算不變的狀況下,一群勞工薪水所得的分布狀況。統計力學能在此發揮作用,是因為模型中勞工的行為模式,可與熱力學中的氣體分子類比:
在熱力學所謂的理想氣體中,每個氣體分子可於限定的體積內自由的移動,而此自由市場模型中的每個勞工,也可於職缺間自由轉換;兩個理想氣體分子在相互碰撞時,其中一個分子的能量會轉移到另一個分子上。同樣的,在總薪資不變的前提下,當兩個勞工職缺異動時,很可能是其中一員薪水增加,而另一員減少。
不過氣體分子是隨機運動的,而勞工則時時刻刻想謀取更佳的職位。
模型中假設勞工謀職的考量主要有三個因素:「薪水」、「勞動成本」和「公平性」。「薪水」無須解釋,扣除勞動成本後的餘額越高,對勞工越有吸引力。「勞動成本」除了包含工時及勞動力等顯性成本外,亦包含練就工作專業所需投入的心血。因此在這個模型中,高薪的職務勞動成本也會提高,與現實生活中需要寒窗苦讀才能從事高薪專業的工作很像。
「公平性」則要舉例說明:假設甲、乙兩人分別是兩間鍋貼店的員工,他們每小時都可以做出60個鍋貼,得到的薪水也相同。若甲的同事們每小時也能做出60個鍋貼,但乙的同事每小時卻只能做出30個鍋貼,那麼就會導致「甲」安於工作,而「乙」想要另謀他職,即便他們的薪水和勞動成本的差額其實是一樣的。
依此模型推算,若這個自由市場運作正常,沒有惡性倒閉的老闆、也沒有靠關係不做事的員工,那麼當每位勞工感到公平時,就是此系統的平衡態。換句話說,「公平性」是這個系統的「熵」,當「公平性」最大化時,系統就穩定了。此外,研究論文也指出這個平衡態,就是賽局理論中的「奈許均衡點」。
在平衡態時,勞工人數對應薪水會呈現「對數常態分布」,大多數的勞工領取略低於平均的薪水,少部份的人領取高薪,大體而言,薪資最高的Top 10%之人,會領走總薪資中25%左右的薪水,其餘的90%勞工會則領走剩下的75%。
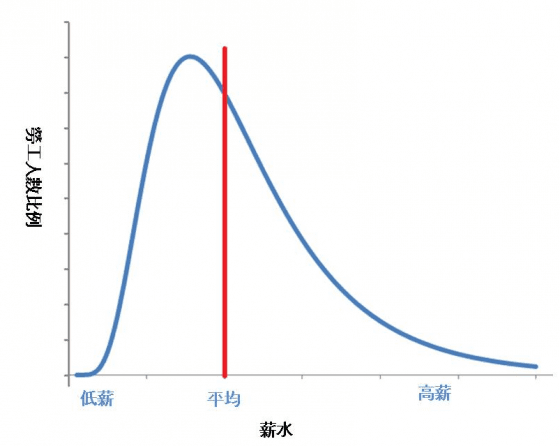
只要那Top 10%的人真的是靠自己付出的勞動成本,而不是靠別人來獲取高薪,那麼這樣的薪資分配應該是公平的。不過我們還是會懷疑,這種純理論的模型真的能反映現實世界的公平嗎?為了要解釋這方面的疑惑,研究人員蒐集了十二個國家的人民所得資料,並套入此模型的數學架構,分析出各國勞工收入分配的公平程度,排名依序為:挪威、瑞典、丹麥、瑞士、荷蘭、澳洲、法國、德國、日本、加拿大、英國和美國。
北歐各國名列前茅,而美國亦不負邪惡資本主義帝國的稱號敬陪末座。這個排名和您心中的印象是否一樣呢?
可惜館主統計力學沒學好,手邊也沒適當的資料,否則真想看看台灣的收入分配會落在排名中的哪個位置哩!
參考資料:
Venkatasubramanian, V., Luo, Y., & Sethuraman, J. (2015). How much inequality in income is fair? A microeconomic game theoretic perspective. Physica A: Statistical Mechanics and its Applications, 435, 120-138.
本文轉載自吳京的量子咖啡館