接下來我要告訴你一個很漂亮的發現,它是在第四世紀初做出來的,當時已是古典幾何時期的尾聲。當中的概念,最早出現於希臘幾何學家帕普斯(Pappus of Alexandria,西元320年前後)的數學著作裡。
首先我得說,要進入這個主題讓我有點惴惴不安,因為它的某些層面相當棘手,我不清楚該如何解釋。(可能有些地方我只能兩手一攤。)
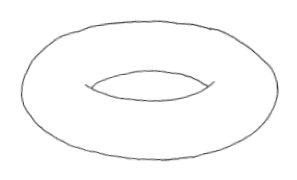
我們從甜甜圈開始談起──呃,我所指的是甜甜圈形狀,不是指甜點。
到現在為止,我們還不真正需要精確描述出形狀。形狀是由平面上或空間裡的點,以某種簡單、賞心悅目的排列方式組成的。我們可說已經很熟悉球體、圓錐或長方形了。那麼甜甜圈又是什麼樣的形狀?
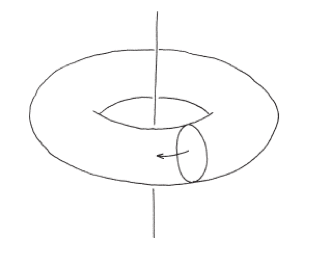
我最喜歡的思考方式,是想像有個圓形繞著空間裡的一條直線旋轉。
這種甜甜圈狀的抽象幾何形狀,叫做環面(torus)。所謂的環面,就是指一個圓沿著圓形路徑在空間中移動所構成的軌跡。
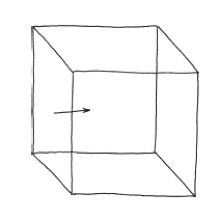
我認為,像這樣把一個幾何形狀描述成另一個形狀的運動軌跡,是很了不起的想法。這不僅產生了類似環面這種新奇的形狀,也讓我們能夠以新的眼光看待熟悉的事物。譬如立方體,就可以看成是一個正方形沿著直線路徑運動的軌跡。
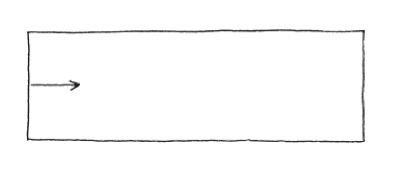
偶爾我喜歡假裝正方形是一隻史前動物,在數百萬年前沿著這條路徑爬行,於是立方體就是牠奮力爬行的「化石紀錄」。我想到的另一個畫面則是雪地裡的足跡。長方形正是一根棍子側向移動留下的「足跡」。
重點是,許多漂亮的形狀可以視為某種運動的結果。
你能不能想出兩種把圓柱體解釋成運動軌跡的方式?
問題是,以這種方式來解釋一個形狀,對於度量是否有任何幫助。描述與量度之間的關係,是幾何學上一再出現的主題。物件的量度會如何隨著描述方式的不同而改變?
尤其,一個物件如果是某個更簡單形狀的運動軌跡,它的量度與這個簡單形狀及其移動方式,究竟有何關係?這是一千六百年前帕普斯提出的問題,而我想要解釋的,正是他的偉大發現。
我就從我們在前面看過的鳳梨片開始好了。
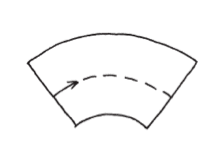
我們現在所講的,是夾在兩個同心圓之間的空間。這種區域叫做環形(annulus)。對於這個形狀,我們很自然會想成是中間去掉了一個小圓的圓形區域。
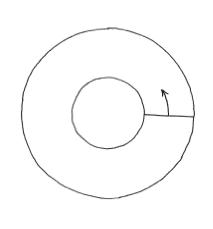
另一方面,環形也可以看成一根棍子沿圓形路徑運動所掃出的形狀,就像鏟雪車繞著一棵樹鏟完雪的結果。
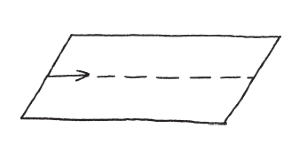
假如棍子(或鏟雪車)是直線行進,當然就會掃出一個矩形。現在我們就能把環形與矩形,視為與同一個概念有關連的不同面貌──此概念就是「由棍棒的運動所形成的形狀」。這很有意思,因為環形與矩形在幾何上大不相同。譬如說,如果你試圖把矩形彎成一個環形,可能不會太順利;內圈的邊會扭曲變形,而外圈的邊會扯破。這情景不大妙。
與環形和矩形有關的有趣問題,就是該怎樣比較兩者的面積。假設我們手邊有根棍子,讓它繞著圓形路徑掃一圈,構成一個環形。那麼需要多長的直線路徑,才能夠掃出同樣的面積?這正是帕普斯想知道的事情。
如果預期正確答案介於環的內、外圓周長之間,這很合理。最自然的猜測是兩圓周長的中間值。我們就假設可以特別安排,讓矩形的長度剛好等於這個「平均」圓周長。那麼兩者的面積一定相符嗎?
結果真的相同。事實上,還有個好方法可以看出這件事,這個方法關連到巴比倫的平方差公式。
概念如下。這個環形完全由內、外圓的半徑來決定。令外圓半徑為R,內圓半徑為r。當我們把這個環形想成兩圓的差,它的面積就會等於。
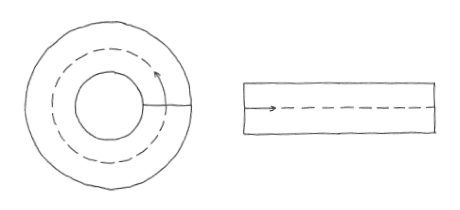
對於矩形,我們需要知道棍子的長度以及路徑長。棍子的長度很容易,就是R – r。知道為什麼嗎?而通過環形中央的圓,它的半徑是內、外圓半徑的平均,所以就此意義來說確實是平均值。換句話說,中間圓的半徑是。
由於圓周長永遠是2p 乘以半徑,因此路徑長(連同矩形的長度)必為
最後,矩形的面積等於長寬的乘積,也就是
恰好是環形的面積。我很喜歡代數與幾何像這樣互相連結起來。屬於代數的平方差公式,由環與矩形的幾何等價關係呈現出來。
不妨把中間的圓形,想成是棍子中心點的移動軌跡。換句話說,中心點行進的距離才是重點。具體來說,我們已經發現,如果棍子的中心點沿著圓形路徑移動一段長度,所掃出的面積會和沿著直線路徑時的面積相同。不管是直線還是圓形路徑,掃出的面積都等於棍子長度與路徑長的乘積。
這個例子正說明了描述(把環形描述成棍子的移動)對於量度(棍子和路徑很巧妙地決定了面積)的影響。就像我先前講過的,幾何學討論的正是描述與量度之間的關係。
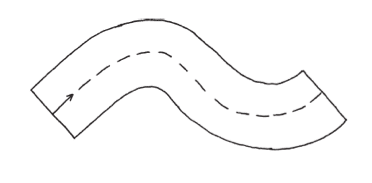
這個例子還可以進一步延伸。假設我們是沿著任意路徑推棍子(的中心點)。
這樣我們仍然會得出同樣的結果嗎?我們仍能說,所掃出區域的面積會和直線路徑的情形相同?面積就等於棍長與路徑長的乘積嗎?或說我們根本就是得寸進尺?
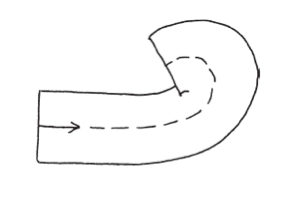
實際上,不管路徑是何形狀,上述的結果都是對的。看我能不能解釋一下為什麼如此。首先可以觀察到,這個結果也適用於圓弧(整個圓的局部)路徑。
這是因為,弧長及所掃出的面積,都會與整個環形的弧長及所掃面積成比例。特別是,對於環形「小段」和非常細的矩形,此結果也會成立。概念就是,把這些小碎片拼組成更複雜的形狀。
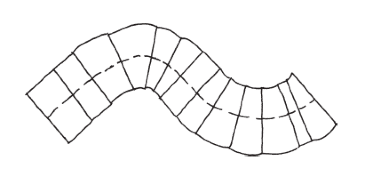
棍子中心點的各種移動軌跡,合起來就構成了一條大的路徑,細部來看是由許多圓弧線段及直線段組成。我們還可以經由適當的安排,讓所做出的路徑盡可能接近我們想達成的路徑形狀。
特別是,我們可以(透過這樣的無窮逼近)讓路徑的總長度,接近我們所想的路徑的長度,而組成小段的總面積,也會接近我們所想的區域的實際面積。由於面積近似值是棍長與路徑長的乘積,且逼近做得越好時,這仍是對的,因此對於我們所想的實際區域,這必然也是對的。窮盡法又幫了大忙。
這正是第一個例子,可說明帕普斯發現的結果適用範圍廣泛:移動棍子而掃出的區域面積,就等於棍長乘上棍子中心點的移動距離。
但有幾個微妙的細節。第一點是,棍子必須隨時與運動方向保持垂直。如果成一個角度斜著推棍子,情況會變得一團糟。
舉例來說,對於歪斜的矩形,帕普斯定理就束手無策了。因為形狀是由小片的環與矩形組成(至少大致上是),而在這些小片上棍子和路徑始終成直角,因此垂直運動是這個方法可處理的唯一一種移動方式。垂直運動正是帕普斯哲學的重要元素之一。
第二個問題是自相交的情形。
如果路徑彎得太劇烈,部分區域就會重複掃過,重疊處的面積也會重複計算。只要保持垂直,並防止急轉彎,就一切順利。
由移動的棍子所掃出的區域周長是多少?