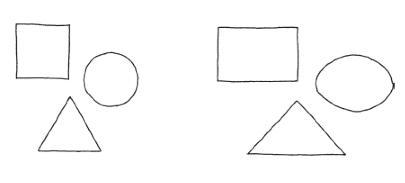我想繼續談一談窮盡法。這個方法的想法,就是想辦法用無窮無盡的逼近,去得到確切的量度,就像我們在前面用無窮多個正多邊形去度量圓形那樣。這是目前為止發明的度量技巧當中,最強大且最靈活的方法。原因在於,這個方法把曲線形狀的量度,簡化為直線形狀的量度。想不到我們竟能精確度量彎曲的形狀,而且還能度量得如此深入而漂亮。
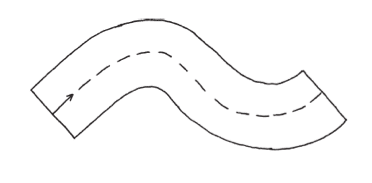
且讓我帶你看另一個例子:用窮盡法度量圓柱的體積。
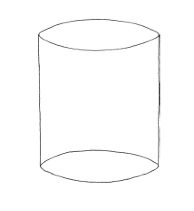
圓柱很有趣,既圓又直,像是介於立方體和球體之間。總而言之,圓柱的兩個底面是(等面積的)圓形,一個在上,另一個在下。
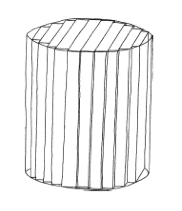
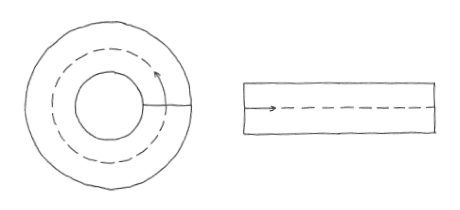
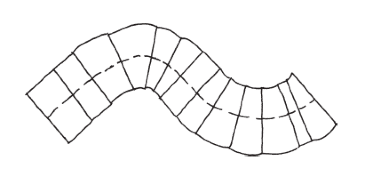
估算圓柱體積的其中一個方法,是想像把圓柱縱切成許多薄片,然後用長方塊來逼近這些薄片。
這些長方塊的長方形底面,可以非常逼近圓柱的底面積。切的薄片越多,長方塊的總體積就越接近圓柱的實際體積,長方形底的面積也越趨近於圓底的實際面積。
好啦,每一個長方塊的體積,等於各自的底面積乘以高,因此所有長方塊的體積,就等於底部所有長方形的總面積乘以高。在此我們利用了「所有長方塊的高都相等」這件事。意思就是,圓柱的體積近似值,會等於底面積的近似值乘上高。
這個模式已經夠我們解讀圓柱的實際量度。切片的數量越多,就能夠越逼近,而長方形底面積與高的乘積,也越趨近於圓形底面積與高的乘積,以及圓柱的體積。所以兩者必定相等,換句話說,窮盡法奏效了。圓柱的體積就等於底面積乘上高。
這讓我想到兩件事。第一,或許你早就知道這個結果了。直觀上不就很容易看出,圓柱所占的空間大小,會與高及底面積成比例嗎?我可不想解釋大家早就知道的事。更何況,把直觀與推理結合起來,這是件好事──也正是數學的本質。
第二件事情是,把圓柱切成這樣的長方塊,似乎很難看又不夠自然。在前面我們度量圓形的時候,是把圓切割成排列得十分對稱的三角形啊。為什麼不沿著中心縱切成三角形楔塊?批評得有理,真的。我用另一個例子來回答這個問題(說得一副我不是提問者似的)。
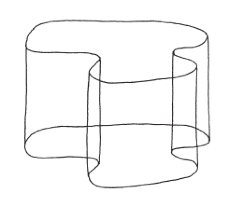
上面這塊立體的製作方式和圓柱相同,只不過上下兩面不再是圓形,而是其他形狀。我們就把這種東西稱呼為廣義圓柱吧。在這個例子裡,根本沒有對稱的切法了,所以最好的辦法只有切成長方塊狀。廣義圓柱的體積,仍會等於它的高乘以底面積。我想說的重點是,無論對稱與否,切成長方塊狀都行得通。這個例子也可以讓你清楚看到窮盡法的靈活度。
(廣義)圓柱的表面積要如何度量?
接下來我想帶你看看窮盡法的威力。在前面我們講過伸縮,也就是僅只沿著一個方向拉長某個倍數。有時候我喜歡把它想成是整個平面的變化,就好像拉著一片橡膠的兩側,而畫在平面上的任何一種形狀,就會跟著拉長。假設我們畫了幾個形狀,然後讓這些形狀(水平)伸縮某個倍數。
你可以看到這些形狀變形得多麼嚴重。拿正方形來說,就變成了長方形(所以四個邊長也不再全部相等)。另外,正三角形變成等腰三角形,圓形變成完全不一樣的形狀,叫做橢圓(ellipse)。
一般來說,伸縮是個很具破壞力的過程,往往會使長度與角度發生嚴重扭曲。特別是,形狀經過伸縮之後的周長,與伸縮之前的周長通常沒有任何數學關係。以橢圓的周長為例,就是個很經典的度量難題,原因正是它和圓周長無關。
另一方面,伸縮卻與面積的變化一致。我們已經曉得伸縮對於面積產生的效應:如果矩形(在平行於其中一邊的方向上)伸縮了某個倍數,它的面積也會乘以該倍率。由窮盡法,我們發現不管是哪種形狀,上述效應同樣適用。若說得更確切些,就假設有某種形狀,我們要讓它沿著某個方向伸縮r倍。我們想知道,此形狀的面積也會變成r倍。
概念就是,要把這個形狀沿著伸縮的方向切成長方條,使得長方條的總面積很接近這個形狀的面積。
伸縮之後,各個長方條也跟著拉長了,所以它們的面積都要乘以r倍。這表示該形狀在伸縮後的近似面積,是伸縮前的r倍。我們會發現,如果讓長方條的數量無限增加(這樣一來,它們的寬度會趨近於零),長方條的實際面積必定也會變成r倍。在嚴重扭曲變形之後,竟然還能掌握面積如何變化,在我看來實在太不可思議了。
橢圓的面積有多大?
同樣的,沿著某方向的伸縮也會讓體積產生相同倍數的變化。知道為什麼嗎?因為長方塊經過伸縮之後,行為仍是規矩的,所以可以如法炮製。當然,我們還是得小心點。比方說,如果一個立體伸縮了2倍,它的體積確實會變成2倍,但是表面積通常就會失控了。不信的話,你可以拿個立方體來試試!
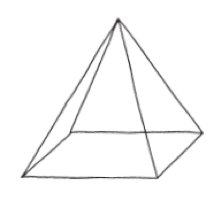
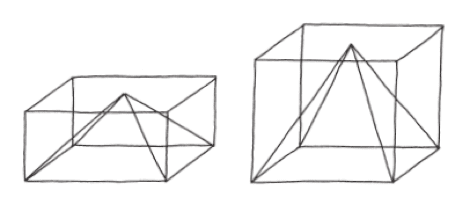
接下來,我要帶你看一個很漂亮的量度(希望這是需要我秀給你看的唯一一種)。我們要度量的是角錐(金字塔)的體積。
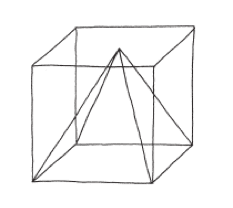
我最喜歡的度量方法,是把角錐放進一個等底、等高的方盒;也就是把這個方盒想成是裝著角錐的箱子。
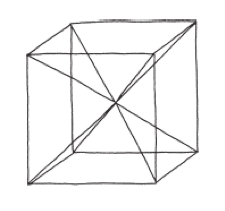
你自然而然就會想問:角錐占了方盒的多少體積?這個問題很難回答,也很年代悠久,最早可追溯到古埃及(那當然)。有個(很聰明的)觀察方法可以做為切入點:如果把一個立方體的中心點和八個頂點作連線,就可以把立方體切成角錐。
切出來的角錐有六個,因為立方體有六個面。這些角錐全都一模一樣,所以體積等於六分之一個立方體。裝著這樣的角錐的方盒,會是半個立方體,因此這些角錐的體積,就等於箱子體積的三分之一。我認為這是個相當漂亮的論證。
麻煩在於,這只適用於上述形狀的角錐(它的高恰好是底邊長的一半)。大多數的角錐可沒那麼恰到好處,不是太陡,就是太低平。
這是不是代表,我們只能度量特定一種形狀的角錐?當然不是!任何一種角錐其實都可以從上述這種特例,經過適度的伸縮變形出來。想要一個更陡的角錐,我們可以讓它任意上下伸縮,想要多高就拉多高。
現在要講到我最愛的部分了:伸縮對於角錐體積和方盒體積的影響,完全一樣。兩者都要乘上伸縮倍率。這表示兩者的體積之比保持固定不變。特殊角錐占了方盒的三分之一,那麼任何一個角錐也必定如此。所以,角錐的體積永遠是方盒體積的三分之一。我太喜歡這一連串概念了。看看窮盡法是多麼博大精深呀。
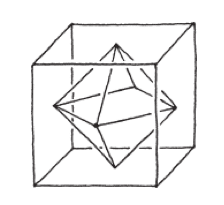
把立方體各面的中心點互相連起來,可以作出正八面體。它占了立方體多少的體積?
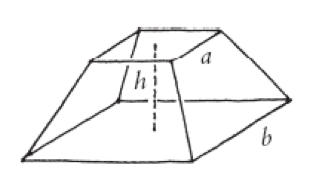
有個不完整的角錐,高度是h,上底是邊長為a的正方形,下底是邊長為b的正方形。它的體積與a、b、h有何關連?
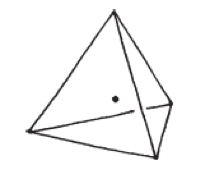
正四面體的中心點在哪裡?