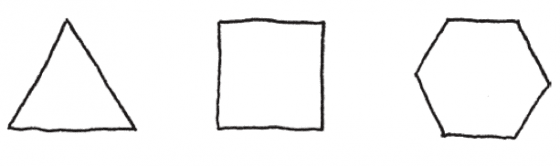
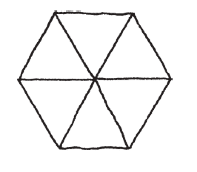
以下是個美麗的圖案。
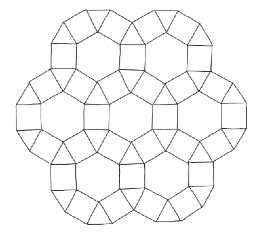
我來告訴你,為什麼我覺得這種圖案很吸引我。首先,裡面有幾種我很喜歡的形狀。
這幾種形狀簡單又對稱,所以我很喜歡。像這樣由直線構成的形狀,叫做多邊形(polygon)。所有的邊與每個角都相等的多邊形,稱為正多邊形。所以我想我應該要說:我喜歡正多邊形。
這個圖案設計吸引我的另一個原因是,當中的組成元件拼接得天衣無縫。鋪磚之間沒有縫隙,也不會重疊(我喜歡把這些元件想成瓷磚,就像馬賽克裝飾藝術)。至少看上去是如此。請記住,我們所談的東西,其實是假想的完美形狀。不能因為圖案看起來很好,便認為就是這麼回事。無論多麼費心製作的圖片,都是實體世界的產物;圖片不可能告訴我們關於假想數學物件的真理。幾何形狀做自己想做的事,不是做我們希望它們做的事。
那我們怎麼能確定,這些多邊形真的拼貼得完美無缺?對於這些幾何物件,我們真能知道些什麼嗎?問題的關鍵是,我們要度量這些多邊形──不是用尺或量角器這類笨拙的實體器具,而是靠心智去度量。我們需要找一種方法,能單單用哲學論證去衡量這些形狀。
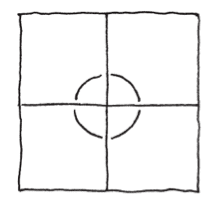
有沒有注意到,在這個例子裡我們需要量的是角度?為了檢查類似的馬賽克拼貼圖案做得出來,我們必須確認在地磚之間的每個接角,各多邊形的角度加起來是一整圈360度。譬如最普通的正方形鋪磚,正方形的各角是四分之一圈,所以四個正方形加起來剛好一圈。
附帶一提,我喜歡用一整圈來當作角度的度量單位,而不喜歡用度。我個人覺得這樣更簡單,也比把一圈分成360等份更自然些(你當然可以選擇自己喜歡的方式)。所以我的說法就會是:正方形各角的角度是1/4。
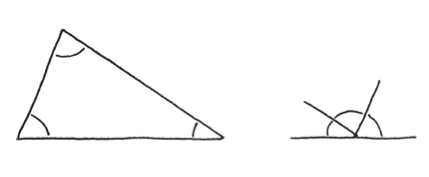
跟角度有關的第一件驚人發現是,不管是哪種形狀的三角形,內角和始終相同,加起來都是半圈(或180度,如果你必須從俗的話)。
如果想實際感受一下,不妨拿紙做幾個三角形,把角裁下來,然後排在一起,你就會看到它們一定能排成一條直線。多漂亮的發現呀!但我們怎麼知道真的就是如此?
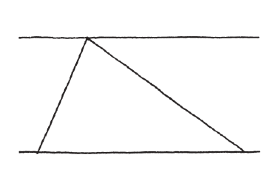
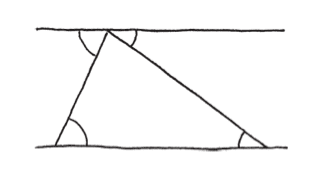
有一種方法是,把三角形改畫在兩條平行線之間。
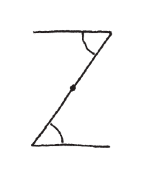
請注意看,這兩條直線與三角形其中兩邊構成的Z字形。(我猜你可能會把右邊的那個稱為倒Z形,不過怎麼稱呼都無所謂。)要請你看的重點是,Z字形的夾角永遠會相等。
這是因為Z字形是對稱的:假如我們讓它繞著中心點旋轉半圈,看起來會完全相同。這表示上下兩個角必定相等。有道理吧?這就是一個典型的對稱論證。如果一個形狀經過了某一組運動的作用之後仍保持不變,我們就可以由此推斷出,兩個或更多個量度必定相等。
回到剛才兩平行線夾三角形的圖示,我們現在曉得,底部的兩個角分別與頂部的對應角相等。
這也就表示,三角形的三個角湊在一起,會在頂部拼成一條直線。所以,三個角相加一共轉了半圈。這個數學推理很輕鬆愉快吧!
這正是做數學的意義。先做出發現(不管用哪種方法做出來都行,包括紙、繩子、橡皮筋之類的實體模型),然後盡可能以最簡單優雅的方式去解釋。這是數學的藝術,也是數學充滿挑戰與樂趣的地方。
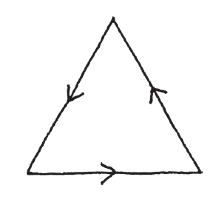
由這項發現產生的其中一個結論是,如果我們的三角形恰好是等邊三角形(即正三角形),那麼三個角會相等,一定都等於1/6。我們還可以換一種方法來看出同樣的結果:想像你是在開車繞著三角形的邊線。
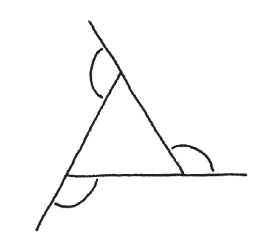
你轉了三個相等的彎之後,就回到起點。由於最後轉了一整圈,因此每個彎必定剛好等於1/3。請注意,我們所轉的角度實際上是三角形的外角。
由於內角與外角合起來是半圈,所以內角和就等於特別是,六個正三角形可以剛好鋪成一個接角。
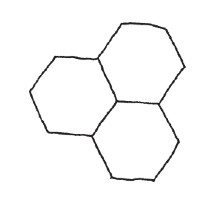
嘿,這不就做出了一個正六邊形!我們額外得到了一個結論:正六邊形的每個角必為正三角形各角的兩倍,也就是1/3。這表示,三個正六邊形可以拼在一起。
因此,我們還是有可能對這些形狀有些認識。尤其是,我們現在明白了為什麼最初的那幅馬賽克圖案拼得出來。
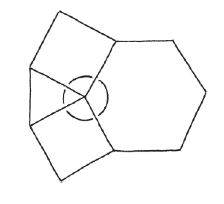
在圖案的每個接角,都有一個正六邊形、兩個正方形、一個正三角形。這些角度相加起來會等於所以拼得起來!
(附帶一提,如果你不喜歡分數運算,你隨時可以換掉度量單位,避開分數。譬如你可以用1/12圈當作單位,這樣的話,正六邊形的角度就會是4,正方形的角度會是3,正三角形的角度是2,那麼相加起來就會等於4 + 3 + 3 + 2 = 12;也就是一整圈。)
我特別喜愛這個鑲嵌圖案呈現出來的對稱性。每個接角都有同樣的形狀依序排在周圍:六邊形、正方形、三角形、正方形。這表示一旦我們檢查過其中一個接角能夠拼滿,就能順理成章推知其他接角也不成問題。這個圖案可以無限往外延伸,鋪滿整個無限平面。我不禁納悶,「數學實在」裡還有沒有其他美麗的鑲嵌圖案?
利用正多邊形做出對稱的鑲嵌設計,方法有哪些?
當然,我們需要知道各種正多邊形的角度。你能不能想想看該如何量出角度呢?
正n邊形的角度有多大?
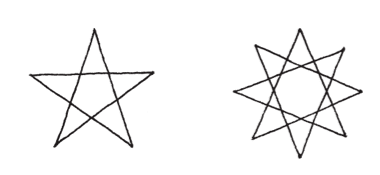
你可以量出正n角星的角度嗎?
從正多邊形的其中一角所畫的對角線,會切割出相等的角度嗎?
雖然我們現在談的主題是多邊形做出的漂亮圖案,我想讓你看看我的另一個最愛。
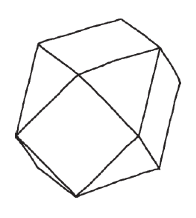
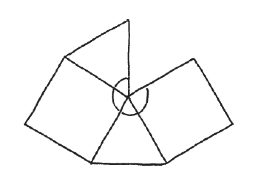
這一次我們用了正方形和三角形,但不是鋪成平面,而是做成某種球形。這種幾何體叫做多面體(polyhedron),幾千年來數學家一直在琢磨這種幾何形狀。思考的方法之一,是去想像多面體展開成平面的模樣。譬如剛才這個多面體,從其中一角展開後看起來會像這樣:
我們可以看到,有兩個正方形及兩個三角形圍繞著一個頂點,但留下了一個縫隙,以便摺成一個球。因此對於多面體來說,角度相加起來必須小於一整圈。
如果角度之和大於一整圈,會發生什麼情況?
多面體與平面鑲嵌的另一個差異點,在於多面體的設計只牽涉到有限多個地磚。模式仍舊可以持續進行下去(就某種意義上),但不會無限延伸到外太空去。我當然也對這些模式感到好奇。
對稱的多面體有哪些?
換一種問法就是:有哪些方法,可把正多邊形做成多面體,而且在每個角可看到同樣的模式?阿基米德找出了所有可能的方法。你能不能找得出來?
最對稱的多面體,當然是每個面都全等的多面體,譬如立方體。這種多面體稱為正多面體。古人已經發現正多面體只有五種(所謂的柏拉圖立體)。你能不能說出是哪五種?
有哪五種正多面體?