從哈伯法開始說起……

• 撰文｜許世穎

本文轉載自 CASE 科學報《整個宇宙，都是我的動物園——天文化學》

整個宇宙就像是一座「分子動物園」，藉由研究的分子光譜，我們可以得知這分子的分佈、溫度等性質；而由於不同的分子有著不同的「習性」，我們還可以得知孕育這些分子的星際環境。

天文化學是什麼？

天文學是研究宇宙間天體的自然科學，除了一般大眾較為知道的「天文物理學」以外，宇宙擁有很多的面向，其中一個就是本文的主題：「天文化學」。

同樣都是研究「物質」的科學，物理學與化學卻是以不太一樣的方式來觀察這個世界。天文化學著重那些宇宙間「不同天體環境中的原子、分子、離子」等，研究它們的形成、分布、彼此之間的交互作用，或是與環境的交互作用。（接下來為了方便起見，我們將分子、離子等統稱為分子。）

天文學雖然是最古早的科學之一，但是天文化學這個學門，則要到 20 世紀中期才開始慢慢出現。理由很簡單：因為分子看不到呀！星星那麼大一顆，用望遠鏡都不一定能看清楚了，更何況是擺在眼前都看不到的分子呢？

因此要研究宇宙中的分子，必須要靠特別的技術才行；其中，最重要的技術之一，就是「光譜學」。

光譜（spectrum）是將光依照波長或頻率排列出來的圖案，像「彩虹」就是一種光譜，是太陽光依照不同頻率分開來的圖案。而光的範疇除了可見光以外，還有很多肉眼看不到的波段，例如無線電波、紅外線、紫外線、Ｘ光……等。

每一種分子都有著屬於自己的光譜，在地球上的我們，如果想要知道分子的光譜長什麼樣子的話，除了可以做實驗量測以外，更多的是用電腦做精密的模擬計算來預測。分子的光譜就像它們的「指紋」，就像警察會將採集到的指紋與資料庫比對，來得知這枚指紋是哪個人留下來的，天文學家則是將觀測到的光譜與資料庫比對，來得知遙遠星際的另一端有哪些分子，甚至是它們的含量、溫度等（圖 1）。

想要了解更多天文學家如何使用光譜學，可以參考：＜把光拆開來看：天文學中的光譜＞。

為什麼宇宙是「分子動物園」？

動物們往往能反應出當地的環境，舉例來說，看到河馬就知道那邊是有水有草的環境；看到櫻花鉤吻鮭就知道有水溫偏低的溪流 ^[3]。將宇宙視為分子動物園也是一樣的，觀察分子的分佈、含量，也可以讓我們回推物理環境。目前，我們已從星際間，觀測到了約 200 多種分子，這裡就介紹幾種常見的星際分子吧！

氫分子（molecular hydrogen, H₂）

宇宙中含量最高的分子，也是「分子雲」的主要成分。分子雲中每一立方公分大約有一萬個氫分子（10⁴ cm^-3）。

分子雲是恆星、行星誕生的地方，所以了解氫分子的分佈，能幫助我們研究恆星形成。同時，氫分子能與較重的元素反應，是許多化學反應的催化劑，產生其他的分子如一氧化碳（CO）、二氧化碳（CO₂）、 氰基自由基（CN）等。

氫分子對天文化學來說相當重要，可惜在分子雲這種均溫只有零下 200 多度的環境，幾乎是不太可能觀測到（因為它是個對稱的分子，有興趣的讀者可以再進一步了解。）^[5][6]

一氧化碳（carbon monoxide, CO）

一氧化碳分佈在星際間低溫、高密度的區域。它是星際間含量第二高的分子。

比起氫分子，一氧化碳容易觀測太多了，所以天文學家更容易從一氧化碳的圖像，來得知分子雲的分佈。由於分子雲幾乎沒辦法用可見光直接觀測，早期的科學家根本不知道我們周邊有這麼多分子雲的存在，直到觀測了一氧化碳的圖像之後才大開眼界。 ^[5][6][7]

氨（ammonia, NH₃）

氨也是很容易被觀測到分子。歷史上第一個觀測到的分子是就是氨。氨有許多譜線，而這些譜線的強度對於環境變化非常敏感，能對應到很多種不同的星際環境。對氨的觀測能讓我們更精確地回推出該處的環境狀況 ^[8][9]。

宇宙中的環境變化太大了，不同的環境下化學反應可能會有很大的差異。宇宙間的發散星際雲（diffuse cloud）、密集分子雲（dense cloud）、恆星形成的熱原恆星核（hot core）等這些已經偵測到大量分子的區域，溫度分佈從 10 K～1000 K（約攝氏 -200 度到 +800 度）、密度從每立方公分一百顆粒子到十兆顆粒子（10² cm^-3～10¹³ cm^-3）都有！

這裡接著再介紹幾種分子含量高的星際環境。

恆星形成區域（star-forming region）

分子雲內部高密度、正在形成恆星的地方。獵戶座 KL 星雲（Orion KL）是獵戶座大分子雲中，恆星形成最活躍的區域。在這裡有許多的「複雜飽和有機分子」出現，如：甲醇（CH₃OH）、甲酸甲脂（HCOOCH₃）等，也有一些長鏈的碳分子，如：氰基乙炔（HCCCN）^[10]。

彗星 67P/Churyumov-Gerasimenko （comet 67P/C-G）

在近幾年的觀測資料中，科學家在這裡看到了含量極高的氧分子（molecular oxygen, O₂），這讓他們感到非常意外。因為氧分子在宇宙中很容易起反應、變成其它的分子，而在彗星這麼樣一個容易揮發的環境中，卻能有高含量的氧分子存在，代表這些氧分子很有可能是在彗星形成的時候，就已經存在周遭的環境中，並且冰封在彗星上 ^[11][12]。

天文化學所牽涉到的範圍很廣，橫跨了許多不同的領域。 整個宇宙就是一座「分子動物園」。天文學家觀察這些宇宙中的分子，來得知遙遠天體中具有什麼樣的環境。星際間也發現了許多有機分子，研究這些分子甚至能幫助我們理解生命的起源，這是現在天文化學研究的一個重點方向。

參考資料

• [1] sci-news / Astronomers Detect Organic Molecules in Starless and Prestellar Regions of Nearby Stellar Nurser
• [2] ALMA / Forest of Molecular Signals in Star Forming Galaxy
• [3] 雪霸國家公園 / 鮭魚與水質
• [4] EAS / The molecular journey from stars to disks
• [5] wiki / Molecular cloud
• [6] COSMOS / Molecular Hydrogen
• [7] NRAO / The Cold Case of Carbon Monoxide
• [8] wiki / Ammonia
• [9] Ho, P. T. P.; Townes, C. H., Interstellar ammonia, Annual Rev. Astron. Astrophys., Vol. 21, p. 239-270 (1983)
• [10] wiki / Kleinmann–Low Nebula
• [11] ESA / Molecular oxygen detected at comet 67P/C-G – ROSINA mass spectrum
• [12] wiki / 67P/Churyumov–Gerasimenko

植物的「硝酸鹽轉運蛋白」為什麼重要？

過去僅知道植物會利用氮肥中的硝酸鹽做為養分來源，而利用分子生物學的技術，可探討植物吸收硝酸鹽的機制，及如何有效利用硝酸鹽等未解之謎。藉由了解轉運蛋白的作用機制，進而提升植物利用氮肥的效率，從最微小的基因尺度，用科學方法來改善農業、環境以及能源等問題。

從大學時開始進入實驗室做實驗，到現在擁有自己的研究團隊，蔡宜芳也帶領著下一個世代繼續研究。她向我們分享這一路走來的點點滴滴，望著窗外一片青綠，蔡宜芳談起為什麼願意投身植物的研究，她笑說：「因為覺得植物很美，植物默默在那邊生長，無怨無悔地提供我們人類養分。」

氮肥吸收暗藏秘密

Q：植物是如何吸收硝酸鹽作為養分，及其中轉運蛋白如何運作？

植物可以吸收的兩種氮源型態為：硝酸鹽、氨鹽。不管是施用什麼形式的氮肥，土壤中的細菌都會幫忙轉換成植物可以吸收的型態。而在土壤中，由於硝酸鹽的含量比較高，所以植物主要是吸收硝酸鹽進入體內作為氮源。

我們在三十年前就知道氮肥很重要，並且多是以硝酸鹽形態被植物吸收，但相關的研究主要集中在傳統生理探討，並不知道在這個機制裡，植物體內負責吸收硝酸鹽的蛋白是什麼。

細胞膜是通往細胞內外的必經路障。而硝酸鹽是帶電離子，無法自己通過由脂質構成的細胞膜，必須由蛋白質的協助才能通過。

1990～1993 年，我在美國做博士後的時候，植物的分子生物技術才剛發展起來。在那之前的實驗多是測植物吸收硝酸鹽的能力；或是在不同環境下，吸收能力變化等較傳統的生理實驗。然而，我們以前都不知道，是什麼樣的蛋白質在負責硝酸鹽的通輸。

因為這個蛋白質很難找，差不多有兩年的時間，我經常整天都坐在電生理實驗檯上。在當時的技術背景下，需要建立新的研究方法。當時的實驗室老闆也曾經一度想停掉這個計畫案，擔心我白白花費太多時間在這上頭，但我想的是既然都作到一半了，就繼續堅持下去。

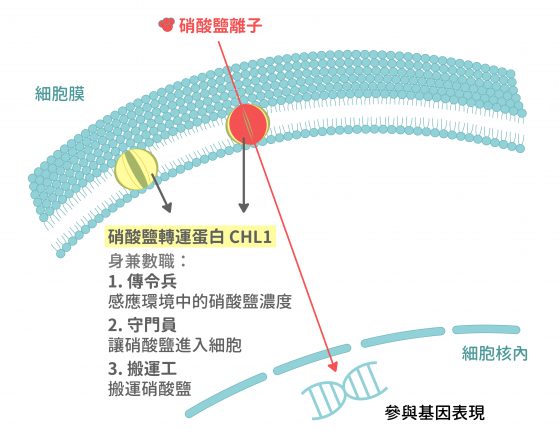
1994 年回臺灣之後，我們團隊陸續發現，位於植物細胞膜上的硝酸鹽轉運蛋白 CHL1 身兼數職。

CHL1 蛋白不僅轉運硝酸鹽進入細胞內進行運用，更會感測土壤環境中的硝酸鹽濃度後，調控下游基因表現來幫助植物更有效率地利用硝酸鹽。透過研究此轉運蛋白，我們可更進一步了解農作物利用氮肥的原理與機制。

植物對環境很敏感，全是為了活下去！

Q：從早期的植物研究方法，到現今的分子生物研究技術，如何在這類研究中進步、成長？

在有分子生物技術之前，多是進行遺傳學或生理學的研究。很早以前，荷蘭的研究團隊就已經找到無法正常吸收硝酸鹽的阿拉伯芥突變株 (mutant)，並開始研究它的生化特性，確認它就是硝酸鹽 (nitrate) 吸收壞掉的突變株，但當時因為沒有分子生物技術，而無法做進一步研究。

我常說，在我十歲的時候這個突變株就在了，可是因為沒有分子生物學的技術，而無法確知是哪個基因出問題導致它無法吸收硝酸鹽。

在 1990 年，分子生物技術剛建立起來，而我就利用這個工具去找。找到這個基因後，我們也開始做一些延伸性研究。由於在植物體內有另外 52 個基因和 CHL1 同屬一個蛋白家族，我們團隊也逐一地去了解它們的基因功能。經過數年研究，了解到植物是如何吸收硝酸鹽進來，而後送往地上部，又如何在不同環境下重新分配不同組織內的硝酸鹽。

我們發現，植物會想盡各種策略來確保年輕葉片有足夠的硝酸鹽，並且在開花結果後，植物也會把硝酸鹽輸送給種子做利用。

這樣一系列的反應都被研究出來後，就可了解硝酸鹽在植物中輸送的各種路徑。

小學跟中學常考的一個植物學考題是：根據教科書的教條，認為無機的氮源(例如硝酸鹽)只會在木質部中輸送，有機的氮源（例如胺基酸）才會在韌皮部篩管中輸送。但是，我們的研究發現教科書的教條需要修改，硝酸鹽可以在韌皮部篩管中輸送，而且這個輸送機制對植物的生長很重要。

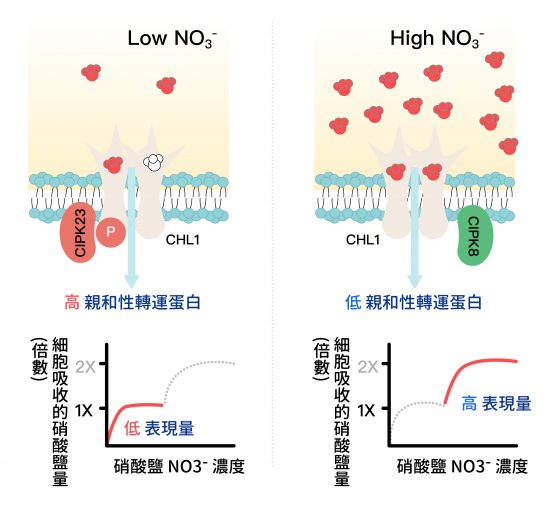
另一部分，我也對蛋白質的調控感興趣。植物本身有兩種硝酸鹽的吸收系統，在土壤硝酸鹽含量很低時，負責作用的系統為「高親和性系統」；在土壤中的硝酸鹽含量很高時，負責作用的系統為「低親和性系統」。植物利用此兩個吸收系統去應對外界多變的硝酸鹽環境。

以前科學家都認為這是兩個獨立的系統，直到 2003 年我們實驗室的博士班學生劉坤祥研究發現：轉運蛋白 CHL1 可藉由磷酸化的轉換，感受到細胞外面的硝酸鹽濃度變化，來調節自身的吸收模式。

這個研究告訴我們：植物有能力感應外界環境的硝酸鹽變化；不只是轉運蛋白會改變，植物也知道濃度低的時候省著點用、濃度高就貯存，因應變化來調控基因表現。這一系列反應很快，三十分鐘就會誘發基因表現。

我曾有一次聽植物鈣離子傳導的演講，演講者說：「實驗發現傷害植物的時候，鈣離子的訊息會增強。」所以會不會有可能當你吃生菜沙拉的時候，植物其實是會痛、有反應的？因為在自然界中，植物不能動，所以它對環境一定要有很好的偵測方法，還有因應策略。不管種子在哪裡發芽，都要想盡辦法在那個環境中存活下來。

改善植物吸收肥料的效率，以利生態環境

Q：過往普遍認知氮肥可幫助作物生長、提供產量，但近年發現氮肥會影響生態、也有食物殘留風險等，這如何能透過生物技術、研究來改善？

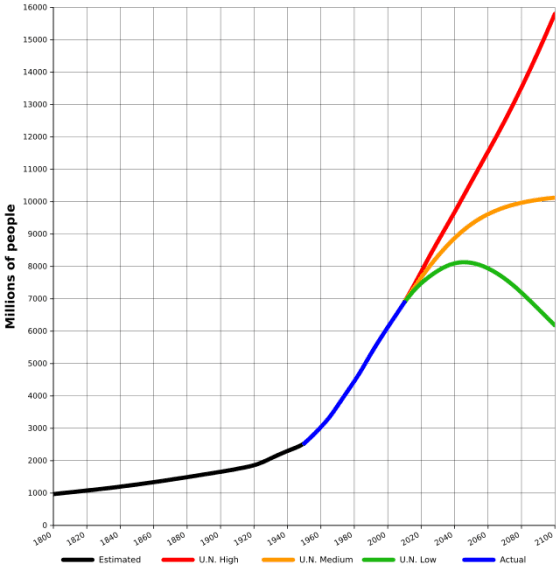
1950 年代的綠色革命發現氮肥可以讓產量翻倍，人口因此開始增加。原本的肥料是取自海鳥糞，後來找到了硝石礦，但仍是不足以應付需求，因此德國化學家弗里茨‧哈伯 (Fritz Haber)找到方法把氮氣轉換成植物能應用的形式。但氮氣的鍵結是很強的，要打斷鍵結要高溫高壓，是非常耗能的事，以至於全世界約有 1~2% 能源是花費在製造氮肥。

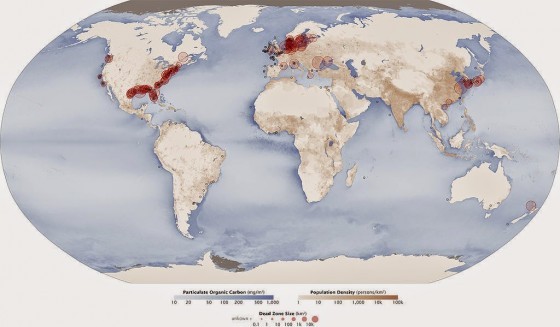
氮肥到土壤裡會被細菌轉換成硝酸鹽，但硝酸鹽不易保存在土壤中，下雨就會沖刷、進入到水循環。如此耗能生產的氮肥，施用下去田間，其實只有一半或少於一半能夠被植物利用。而湖川海洋中過多的硝酸鹽會造成優養化作用，形成藻華、Dead Zone，這其實是全球性的生態影響。

因此，我們希望想辦法解決這個問題，讓植物吸收硝酸鹽的效率好一點，進而減少環境的汙染、製造氮肥的能源消耗。

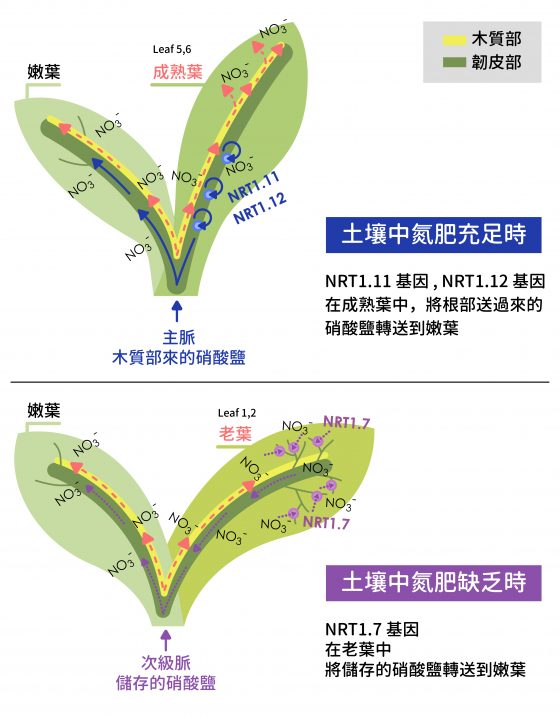
氮肥供應充足的時候，硝酸鹽養份主要會送往成熟葉；但在缺乏氮肥時，植物會把儲存在老葉的硝酸鹽運送到嫩葉。看到這種轉移的情況，我們就想：如果能夠強化這種轉移養分的機制，是不是就能夠加強氮肥的利用效率？

如下圖，我們研究發現，葉子中有一個 NRT1.7 基因有這個作用，如果能加強 NRT1.7 的基因表現，或是活化參與這個轉移機制的蛋白質活性，就可以提高植物利用氮肥的效率，進而促進植物生長。目前已經在阿拉伯芥實驗成功，也已取得臺灣和美國的專利，現在則是在水稻、菸草上進行試驗，這其實是個很漫長的過程，但一旦成功，對於生態環境是一大助益。

對我來說，要一直用新的技術來回答新的問題，因為新的技術一定能夠讓問題的答案更深入，但我認為最重要的還是找到你要問的問題。而我最想問的問題是：植物是如何去處理它的養分，來做它最好的生長反應？研究過程中經常解決了一個問題後，還會有下個問題。

我一直喜歡植物研究的一個特色是，你可以從分子生物的尺度、到整株植物的生理去探索你的問題的答案，並發現這一切都相互呼應。

因為太專注於分子生物層面的東西，有時候是細微到只看到蛋白質的交互作用，但這樣細微作用如何影響到整個作物的生長，甚至是最後到農業的產量，這是我最感興趣的。

不只是學術，科學研究的重重挑戰

Q：當初為何會投入植物、科學的研究？

我覺得投入研究的重點是「好奇」。你一定要有好奇心，會想追求一些新問題的答案。一名科學家必須要有好奇心，同時也需要有你的邏輯思考能力去尋求答案。

我大學是台大植物系的，會就讀植物系其實是個很浪漫的原因──只是因為我很喜歡植物而已。我喜歡走進森林的感覺，讓我很想去了解植物。

大四時，進到實驗室是做組織培養，那時候是很熱門的題目，因為很新奇。植物組織加入不同荷爾蒙，就會變成地上部的葉子或地下部的根，那是由於植物細胞有全能分化的能力。組織培養雖然有趣，但知其然不知其所以然，完全不知道是什麼原因造成這些變化，無法滿足我喜歡打破砂鍋問到底的個性，所以碩士就開始就往分子生物的領域走。不過因為那時植物的分生研究還沒發展起來，我就先從研究酵母菌開始，把分生基礎打好；等到讀完博士班，開始找研究題目、看論文時，發現仍是植物相關研究最能觸動我的神經，所以我就決定要再回去研究植物。

我覺得在科學的養成上，技術是一環，但邏輯思考的養成比技術的養成更難。邏輯思考的養成更要慢工出細活，很難一步到位。

看論文時，去找到這篇論文的核心價值是很重要的。做研究還要知道在這個領域中，最重要的問題是什麼。畢竟，找到問題後就是賭博了。要知道哪個方向的研究值得投資，要知道實驗資料和數據所代表的意義是什麼，如何解讀數據也是很重要的邏輯思考訓練，這些將都會成為你設計新的實驗時的依據。

其實，最辛苦的是剛開始設立自己的實驗室的時候。因為要訓練人，不是自己做就好，還要承擔所有的成敗。而且科學也是需要對外溝通，告訴資助單位、期刊還有大眾這個研究的重要性為何。

女性從事科學研究有多一層的考驗，因為社會對女性有許多的期許與要求，要兼顧家庭、事業兩方會是蠻大的挑戰。我覺得我算是蠻幸運，先生對我支持度也很高。在很多時候，女性碰到在家庭跟事業之間做抉擇時，會較容易放棄自己的事業。因此我常跟女學生說：對於家事能夠取得幫忙，就去取得，妳可以克服的，女性也可以顧全自己的事業。

延伸閱讀：

• 蔡宜芳的個人網頁
• 蔡宜芳的實驗室網頁
• 〈如何為植物調配五星級的營養特餐：談植物對於硝酸鹽 (Nitrate) 的吸收〉，作者：許博凱、蔡宜芳。《中央研究院週報》，第 1119 期。
• 〈身兼數職的硝酸鹽轉運蛋白〉，作者：郭朝禎。《科學發展》，2012 年 5月，473 期。
• 【第 11 屆臺灣傑出女科學家獎得主影片】臺灣綠色革命女強人，開創生物經濟契機
•  Liu, Kun-Hsiang, and Tsay, Yi-Fang. (2003) Switching between the two action modes of the dual-affinity nitrate transporter CHL1 by phosphorylation. EMBO J, 22:1005-1013.
•  C.-H. Ho, S.-H. Lin, H.-C. Hu, and Y.-F. Tsay* (2009) CHL1 Functions as a Nitrate Sensor in Plants. Cell 138, 1184–1194. (Recommended by Faculty1000, 12 stars)
•  S.-C. Fan, C.-S. Lin, P.-K. Hsu, S.-H. Lin, and Y.-F. Tsay* (2009) The Arabidopsis Nitrate Transporter NRT1.7, Expressed in Phloem, Is Responsible for Source-to-Sink Remobilization of Nitrate. Plant Cell 21: 2750–2761.
•  Y.-Y. Wang, P.-K. Hsu and Y.-F. Tsay* (2012) Uptake, allocation and signaling of nitrate. Trends in Plant Science 17:1360-1385.
•  J. I. Schroeder *, E. Delhaize, W. B. Frommer, M. Lou Guerinot, M. J. Harrison, L. Herrera-Estrella, T. Horie, L. V. Kochian, R.Munns, N. K. Nishizawa, Y.-F. Tsay, D. Sanders* (2013) Using membrane transporters to improve crops for sustainable food production. Nature 497 (7447):60-66.
•  Ya-Yun Wang∗, Yu-Hsuan Cheng∗, Kuo-En Chen and Yi-Fang Tsay (2018) Nitrate Transport, Signaling, and Use Efficiency. Annu. Rev. Plant Biol. 69:27.1–27.38.

本著作由研之有物製作，原文為《找到植物吸收養分的關鍵──專訪蔡宜芳》以創用CC 姓名標示–非商業性–禁止改作 4.0 國際 授權條款釋出。

本文轉載自中央研究院研之有物，泛科學為宣傳推廣執行單位

在網站上看不過癮？研之有物出書啦！

《研之有物：穿越古今！中研院的25堂人文公開課》等著你來認識更多中研院精彩的研究。

自從幾年前開始教通識課以後，對於許多課程要怎麼教，開始有了不同的想法。怎麼說呢？一般專業課程總是強調「專業」，舉個例子好了，學過國高中化學的同學應該都知道哈伯法（Haber-Bosch Process），在高溫高壓下以鐵粉做為催化劑將氮氣與氫氣轉化為氨（ammonia）：

通常化學課的時候，老師只會提到，因為氮氣(N₂)的兩個氮原子之間是三鍵，所以要打開氮氣很不容易；因此不但要用高溫高壓，還要用鐵粉當催化劑…

然後？就沒有了。講完了。

但是，哈伯法偉大的地方就只是這樣嗎？哈伯（Fritz Haber）因為發明了這個方法，得到1918年的諾貝爾化學獎。難道就是因為他成功的打斷了氮-氮三鍵而已嗎？

當然不是。哈伯法的重要性在於，從此人類打開了以人工提高作物產量的大門，農作物的產量從此大大的提高。

當然，產量提高其實也是有限度的，在植物的營養上，有個名詞叫做「關鍵濃度」（critical concentration）。當土壤中的養分低於這個濃度時，植物的生長與養分的濃度成正比；超過這個濃度以後，植物的生長跟養分的濃度就不成正比了，也就是說，用再多也沒有明顯的效果。

但是，在過去只能使用天然肥料（動物的屍體、糞尿、植物的落葉等）的時代，由於天然肥料必需要等待微生物分解（這部分在堆肥時已經大致完成），再經過土壤中的微生物將其中含氮成分分解為硝酸根（nitrate，NO3-）與銨離子（NH4+）後，才能為植物所吸收，因此效果緩慢。加上為了方便起見，農人們總是會以單作（monoculture）的方式來種田，這種在大片的土地上種植單一作物的方式，很容易會使土壤缺少某些特定的養分（尤其是氮與磷），所以在哈伯法還沒有出現以前，要提高土壤內的氮濃度，除了使用天然肥料之外，就只剩下使用綠肥，或是與豆科植物輪作了。

但是，這些方法，都不能使土壤中的氮的濃度超過關鍵濃度；因此，當哈伯法出現之後，農夫將化學肥料施放在田裡，立刻有了奇效–農作物的產量大大的提升。加上育種改良以及殺蟲劑、除草劑的使用，20世紀小麥與稻米的產量提升了8-10倍（平均產量是4倍）。

但是哈伯法對於科學界的貢獻，並不僅僅在於農作物產量的提升；在哈伯發明化學固氮之前，一直有一派學說認為，這些在生物體中的化合物，只有生物才能合成（也就是所謂的生機論Vitalism）。雖然生機論在科學上的地位在1828年在維勒（Friedrich Wöhler）合成尿素以後，已經岌岌可危；但是直到哈伯法出現以後，生機論才不再被提起。

但是哈伯法對全人類最大的貢獻，還是在於：從此想要多少氮肥，就可以製作多少氮肥。雖然在十九世紀Sach等人的研究，已經使大家了解，要能夠正常的生長與繁殖，植物需要17種元素（稱為必需元素essential element）；但是其中最關鍵的氮與磷，卻始終無法足量提供給植物。

但是，大量的施放氮肥，卻造成了另一個效應：死亡海域（Dead zone）。

死亡海域最早出現在1970年代。由於化肥的大量施用早在1930年代就開始了，因此也花了一些時間去釐清到底是怎麼回事。簡單來說就是，大量施放氮肥（主要是硝酸根）與磷肥（磷酸根）到土壤中，但是土壤主要是由矽酸鋁顆粒構成，也是帶負電的，所以同性相斥使得氮與磷無法久留在土壤中，很容易隨著雨水、灌溉水流到附近的湖泊與河流裡，最後流到海裡。

當海裡的氮與磷濃度上昇以後，造成藻類大量生長，形成藻華（algae bloom）；藻華隔絕了水下植物的陽光，使得水下植物開始死亡；植物的死亡與分解吞噬了水中的氧氣，接著動物開始死亡…然後就是死亡海域。

由於慣行農法的單作、密植，使得化肥成為農業的必要之惡；所以死亡海域一直都是難以解決的問題。2008年的統計，全球的死亡海域共有405個點；而死亡海域的「熱區」集中在人煙稠密的北半球。

而施放化肥加上灌溉，除了造成死亡海域之外，又會使得土壤酸化、鹽化。雖然哈伯法似乎在短時間內提高了農作物的產量，養活了許多人（這可以由1940年代開始，世界人口急速上昇看出來）；

但是，哈伯法所造成的副作用，包括死亡海域、土壤酸化、鹽化，以及因為人口大幅增長造成土地大量被開發的生態破壞等等…究竟是功是過呢？其實科學家發明了新技術，而這個新技術在大量被使用之後，產生了意想不到的變化，我想這也是當初哈伯始料未及的吧！

本文轉載自作者部落格

參考資料：

1. Taiz and Zeiger, Plant Physiology, 5th ed.
2. Laurance Mee. 拯救死亡海域。2006。科學人。
3. Wikipedia. World population, Dead zone.

氨燃燒可產生能源，作用後僅產生不會對環境造成污染的氮和水。但是氨合成須在高溫高壓下進行，耗費大量化石燃料，得不償失。根據中廣報導（轉引自Only Perception），東京大學「催化反應工程學」副教授西林仁昭團隊成功研發新技術，可透過含「鉬」的化合物作為催化劑，使氨合成在常溫常壓下進行，不需使用任何其他燃料，大幅減少成本。