文/黃敏晃 台大數學系退休教授
攝影/陳淳廉、任明芬
1. 對稱不對稱
有些朋友知道筆者左腳踝受過傷,行動不便。即使拄著拐杖,還是不利遠行(走路超過半小時,腳踝就會痛)。故在台大校區附近,我總是騎著單車活動。估計每天在單車上的時間,約有兩小時之久,這當然包含我刻意騎單車運動的時間。其實,台大校園裡各條主要道路騎一趟,就要花45分鐘以上,更不用說許多偏僻小徑尚可一遊。
長期練習,使我騎車技巧精熟。有次在台大校園裡,來個轉彎急煞車,停在老友黃榮村教授(台大心理系,曾任教育部長,現任中國醫藥大學校長)面前跟他打招呼。第二天到國科會開會,他見到我拄著拐杖蹣跚走路的模樣,根本不相信,直呼我騙人,乘公車、搭捷運時騙年輕人讓座。事實上,騎單車動到的是膝蓋,腳踝完全不受影響。我左腳踝的傷勢,還是有妨害到我騎單車,特別是上、下車的時候。因為一般人騎車的習慣,都是用左腳做為上、下車的支點(單車的設計是左、右不對稱的),而我的左腳踝常支撐不住我的體重(很不幸的,超過80公斤,且有越來越胖的趨勢)。於是我只好調整上、下車的方式。
我下單車的方式如下:在單車輪子停止滾動後,右腳著地,左腳跨過車頂,在單車右邊立定後,把單車牽到可以倚靠的地方如牆邊、樹幹旁等,手放開車把手小心走到車左邊去停車(單車的停車支架設在車左邊)。上車時則先用握住車把手的雙手,支撐部分的體重,把右腳跨到車右邊地面(我的單車屬舊式的淑女車,座墊前方沒有直槓向前連結單車把手軸),右腳用力把屁股撐上座墊,左腳踩踏板使車前進。
我想過,人是左、右對稱的,習慣使用左手右手,或左腳右腳,應是人進入社會後受到部分影響而形成的(當然有人是天生慣用左手的)。若加以訓練,我未嘗不可以模仿從左邊滑行上車的方式,從右邊上車。於是,我在腦中運用想像力,形成我從右邊上車的腦圖(mental map,是連續動作的動畫)。然後,人到單車右邊,右腳去踩踏板(想用左腳蹬地使車滑行),但在地上的左腳踝立刻感受到體重的壓力,使我無法站立而摔倒在地。這次並沒受傷(小小的皮膚擦傷不算),但沒第二次的嘗試。
這次失敗並未推翻我認為人體結構(一般而言)是左、右對稱的信念。我記得小時候為了學騎單車,摔過N次後終於成功。故我只要肯再接再勵,是會成功的。但據說,老人多有骨質疏鬆的症候,怕摔,故想了又想,沒敢繼續練下去。這恐怕是老人最大的毛病,想的太多,做的又太少。
2. 鄰域的概念
數學裡有門學問,叫做點集拓撲(Ponit Set Topology)。高等微積分裡會講一些入門,在大學數學系的三、四年級也常開一門專課(3學分)。它的主旨在定義一個更寬廣的理論架構,使我們可以將連續(continuity,以及之後的微分…,故研究所可以開differential Topology的課)這個概念延伸到歐幾里得空間Rn(這是數學裡習慣用來表示n維歐氏空間的符號)之外的空間去。這門課中有個概念叫做鄰域(neighborhood─函數連續的初淺意思就是,其值在任何的鄰域中變動不會太大),我騎單車時常體驗到鄰域在日常生活的意義。我的鄰域就是居家附近,常去的場所,輕易方便就可到達的地方,我喜歡拜訪的區域。這樣的鄰域會隨著你所使用的行動方式而改變。比如說內人,她是步行的,故她的鄰域就是台大校園(我們住的宿舍在台大校園的邊陲地帶),和周圍二、三條街以內的區域。我的交通工具是單車,鄰域就擴充到二二八紀念公園旁的台大醫院(看病),市北師(上課)和植物園(建中),以及在市民大道東端盡頭的漢聲出版社(開會),單程約為半小時。
在台大校園內、外騎單車的最大差異是,校外我常騎到人行道上,避免跟汽、機車爭道,以策安全。最近聽說,台北市有要通令「禁止單車騎上人行道」的意圖。若然,我是寧願挨罰,也要騎上人行道的。我撞行人,他最多輕傷;我被汽、機車撞到,起碼重傷收場。
目前,全世界都公認騎單車是最符合節能減碳的環保交通方式,歐洲大多數的都市,為了鼓勵騎單車上、下班,做了許多方便單車族的措施。台北市不但不積極籌謀這方面的方案,反過來要通過對單車族不友善的法令,是會被選民認為行政不力(跟不上時代潮流)的。在沒有單車專用道的狀況下,把道路分成汽車道和人行道,機車和單車需要被定位,屬於哪類?若認為自然的人體之外的道具,就不屬於人行道,則拄枴杖,坐輪椅者該到汽車道去,絕對不合理。另一種方式是用速度分類(不等級的速度容易產生車禍),則可先參考下列事實:
1. 人的步行速度約每小時3~5公里。
2. 單車的速度約每小時12~20公里。
3. 機車的速度約每小時40~60公里。
4. 汽車的速度約每小時50公里以上。
顯然,機車和汽車的速度是相當的,故它們使用相同車道是合理的。單車的速度是人步行的3到5倍,而汽、機車的速度又是單車的3到5倍,所以單車的歸屬是較尷尬的。故歐洲人特別設立單車道,有其道理。若無單車專用道,又該如何?通常我騎單車上人行道時,都故意放慢速度(時速低於10公里),因此不易發生撞人事件。也許這就是一種解法,騎上人行道的單車,速度不准超過時速10公里。
3. 一般狀況
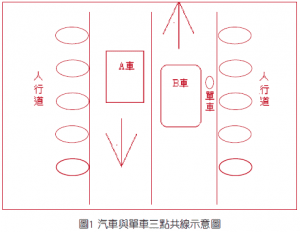
在校園內騎單車,因汽車速度慢(限速30公里每小時),又禁止機車入校(只有校警的機車可在校園內行駛),故我覺得應該用最高的標準(道德?)要求自己,即不騎上人行道。身為學校的老師,行為最好不要有任何瑕疵,讓人非議。但如此的結果是常產生「三點共線」危機如下,如圖1所示:
若兩部汽車相閃而過的剎那,你騎著單車剛好在邊上,即兩部汽車和你的單車形成一直線,而且此直線恰巧垂直於道路的邊線(保證空間最擁擠)。這種場景若發生在寬濶的椰林大道,一點問題都沒有。偏偏台大有許多路,比一般的兩線道還窄,兩部汽車相閃都要很小心(減速),你還要騎單車跟他們擠在一起。每次,我都恨不得是騎在人行道上。幾次經驗後,我的解法是不讓這種事件發生,即我察覺到它有可能發生時,會故意騎快或騎慢,避免「三點共線」的現象。
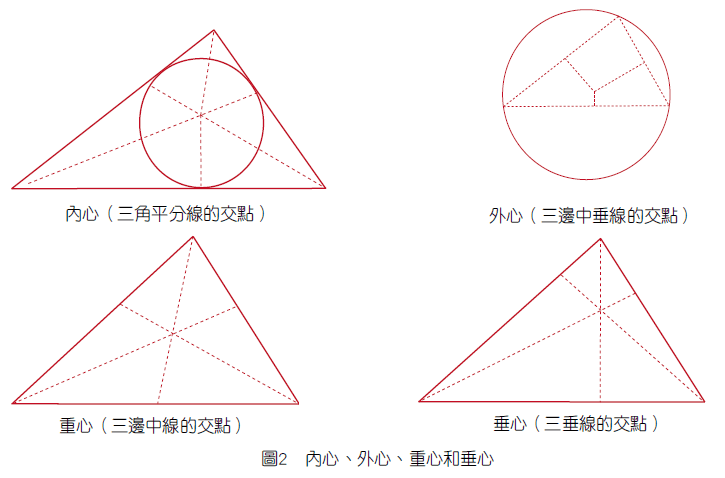
「三點共線」和「三線共點」是國中幾何教材裡必見的教材。這些教材的要點是,當此特殊狀況(或很強烈的條件)發生時,表示相關的幾何物件之間的相對位置關係,形成緊密結合的結構體(比如說,三角形是最堅固的幾何形,故其三條內角平分線會交於一點,叫做內心,以及外心、重心、垂心等都是三線共點的特例(見圖2))。
問題在於交通事務中,產生關係的物件一定包含人和車輛在內,這樣的物件要互相間,或和其他硬體如橋樑、圍欄之類的物件產生緊密的相互位置關係時,大概就有點危險了。故道路的設計當然避免三條道路交於一點的狀況(以前喜歡用圓環處理,但效果不佳,現多廢除),而希望它們在一般的狀況下。
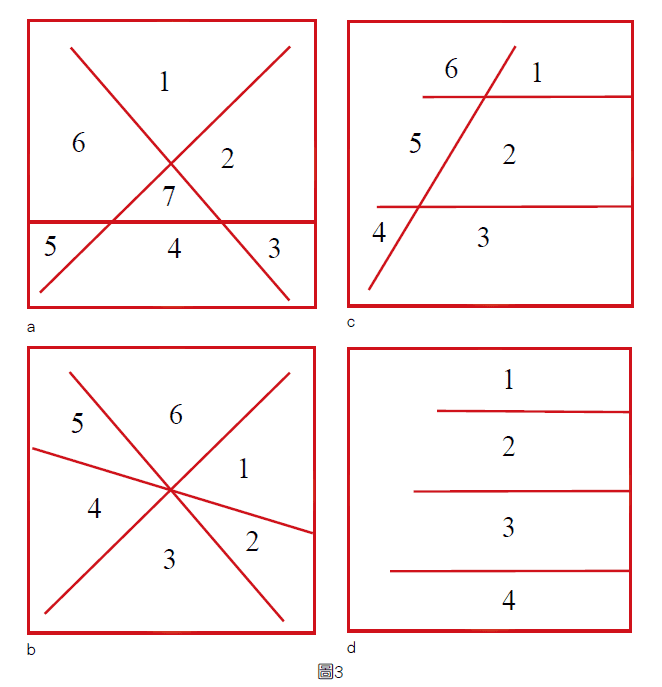
所謂的一般狀況(position in general),就是這些幾何物件可以合力產生最大的維數,如在一般狀況的三點可決定一個維數平面,及四點可決定一個三維空間;或最大的分割數目,如在一般狀況的共平面三條直線可將它們所在平面切割成七塊,如下面圖3a圖所示,三線共點或有平行現象發生時,平面被切割出來的數目,都會比七小。
下面有如下兩道題目給讀者作進一步探索:
(1) 在同一平面上的n條直線可把這個平面切割出的最多塊數( 如一條兩塊, 兩條四塊,三條七塊)是多少?
(2) 將上題延伸到三維,n個平面可把空間切割出最多部分是多少?
最後,出個題目讓讀者想想,或做實驗來探索。筆者有次騎單車,輾過一攤油漆,騎了一段路後回頭看,只見車輪留下的痕跡,好像有些規律(見圖4)。這個規律是如何的?它跟車輪的大小(如前輪小於後輪或是前後輪一樣大)有關嗎?它與兩輪之間的距離有關嗎?
本文原刊登於《科學研習月刊》No.50-5