
一個人的姿態很重要。
舉手投足,不僅影響到他人對自己的第一印象,根據研究指出,甚至會影響到自己的心情。好比說,如果開會前做出「信心滿滿、雙手叉腰」的姿勢一兩分鐘,言談將會更有自信,要是彎腰駝背,會讓人下意識地變得更怯懦。佛家也很強調姿態的重要,提出「四威儀」:
立如松、行如風、坐如鐘、臥如弓。
佛家認為,時時注意自己的姿態,就是一種隨時隨地的修行。然而,生活中有許多處境艱難,讓我們無法好好恪守四威儀,特別在梧桐花開的五月,或是整天蟬鳴的七八月,那是梅雨、颱風的季節。
在雨中撐傘還要立如松,行如風,除了心性的修行,恐怕還需要數學的輔佐。
※
請想像一下這樣的畫面:一位大和尚和幾個徒弟四處化緣,他們走在一望無際的草原上。天空中厚重的烏雲,忽然像被人擰過了一般,下起了雨。眾人撐起雨傘,繼續前進。一會兒,雨勢轉驟,颳起風來,就算撐傘,眾人的綁腿依然被雨水打濕,變成深色。大和尚問了個子最高的高徒弟,有沒有看見前方有村落。高徒弟搖了搖頭。
大和尚注意到高徒弟將傘撐得很低,甚至弓起了背,整個人彎腰蜷縮在傘底下。勉強要說是立如松,也只會讓人聯想到景觀盆栽裡曲折蜿蜒的老松。他搖了搖頭,怎麼這些徒弟不懂得觀察師傅呢。
「徒兒們,看看為師,不彎腰駝背,身上一點也沒濕。」
仔細一瞧,大和尚身子挺得筆直,傘也舉得老高,但下擺乾乾的,一滴雨水也沒有。
「因為師父比較矮?」
大和尚愣了一下,臉上閃過一片紅色,他回答
「雖然這是事實,也是原因之一,不過不是關鍵。重點是,面對雨水的迎擊,不需要讓自己變矮,變小。只要懂得『後退』就好。」
「師父在說禪嗎?」
「不,我在說數學。」
大和尚用手杖在地上畫了一幅圖
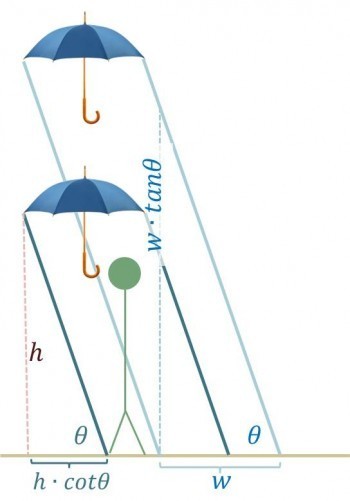
「這是我們在雨中行走的截面圖。假設雨跟地面夾角為θ,拿傘的高度為h,傘的寬w。
你們看,當雨是斜的,傘的遮蔽範圍將從長方形變成平行四邊形,傘正下方h.cotθ的範圍都會被雨淋濕。傘拿低一點讓h變小,的確有幫助。但更正確的方式,應該是往後退h.cotθ,即可確保褲管不會被淋濕。」
大和尚頓了頓,繼續說:
「不是常跟你們提起,要時時注意四威儀,『立如松、行如風』嗎。只要懂得這個道理,雨天不用駝背走路,還可以將傘舉得更高,更英挺,只要算好後退距離,依然得保全身不濕。」
徒弟們照著師父的話做了後,雖然傘舉再頭前,看起來有點像和尚版的自由女神像,但綁腿的確不再被雨淋濕了。正當大夥兒讚嘆師父博學多聞時,高徒弟發問
「師父,徒兒腳沒濕,可是臉卻濕了。」
眾人一看,只見他臉上滿是雨水,甚至僧袍領口顏色都變深了,那模樣有些滑稽。大和尚笑了笑,低聲說
「誰叫你長那麼高,活該。」
「師父說什麼?」
「噢,沒有。為師說,因為你長太高了,要是雨打得斜,註定會被淋到的。從方才圖的例子可以看到,要是傘拿低一點,遮雨的高度跟傘高度一樣是h,但當傘拿高一點時,遮雨的高度即是w.tanθ,竟然跟傘的寬度w和雨的斜度有關。而遮雨的高度是(h,w.tanθ)兩個數值取較小值。換句話說,只要身高高於w.tanθ的人,終究難逃被淋溼的命運。往後退,就像你現在這樣,腳不濕,但上半身卻淋溼了。」
大和尚邊說,邊用手杖又畫了個圖
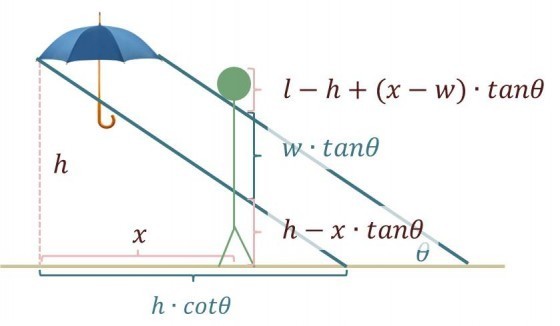
「這時,只好做出取捨,要讓褲管淋溼多少?頭淋溼多少?這樣的取捨可以靠調整傘的高度,和後退的幅度來達成。除了雨斜度θ、傘舉的高度h、寬度w,再假設三個數字,後退幅度x,身高l,以及褲管會濕掉的高度z。z可以利用相似三角形的概念求得
也就是說,褲管直到h-x.tanθ的高度都會濕掉。中間身體w.tanθ的部分不會濕。上半身從天靈蓋往下l-h+(x-w).tanθ的部位都會濕掉。」
大和尚將自己背上遮陽的斗笠卸下,遞給高徒弟
「你算好後,再調整斗笠戴的位置跟角度,用斗笠遮住上半身的雨勢吧。駝背讓l變小,的確可以降低淋到雨的部位,但有違修行,還是別做了。」
※
走了一個時辰,雨勢不但沒趨緩,上天彷彿在考驗眾人,還加強風勢,讓雨變得更斜,這下,除了最高的徒弟外,其他人也紛紛戴上斗笠,除了大和尚依然不用。
意外發現「原來我最矮啊」的大和尚,看著這些徒兒為了恪守他的教訓,在雨中不駝背,雖然還是有些氣他們怎麼都那麼高,活該被雨淋,但想了想,還是決定再傳授他們一道心法。
「把傘拿斜吧。」
「拿多斜呢,師父。」
「跟雨勢垂直。」
大和尚又拿起手杖,在地上畫著。
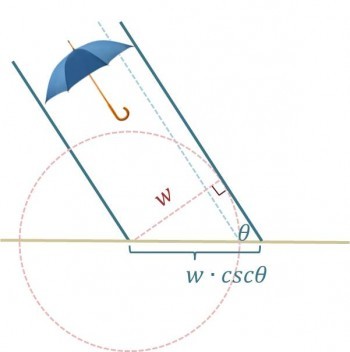
「我們可以用這圖來證明『傘與雨勢垂直』為最佳拿法。將傘一端投影到地表上的點為圓心,傘寬為半徑,可以畫出圖中的圓。再給定下雨方向為斜率,過圓上一點,符合『點斜式』所需條件,即能畫出一條直線。直線跟地表相接的點,與圓心之間的距離是避雨區域,水平拿傘時,此區域長度是w。乘上tanθ,即得到可遮雨高度w.tanθ。現在,當傘拿的角度與雨勢垂直,這條線就會變成圓的切線,通過圓上一點,線跟圓心的距離最遠,避雨區域最大,變成w.secθ。」
大和尚抬頭看,每一位徒弟,臉上沒被雨淋到,卻濕淋淋地「一頭霧水」。他只好換個方式解釋
「你們試試看,從原本水平拿傘,慢慢變斜,會淋到雨的部分越來越少,在某個角度會達到最大值,之後再更斜時,反而又會變小。對吧?」
徒弟們轉動手腕嘗試,點頭回應師父。
「再看剛剛地上這張圖,要是傘跟雨勢不垂直,這條線會變成割線,和圓相交兩點,要是這個角度是最大值,就表示有另一個角度也會提供最大的遮雨高度,兩個最大值,違反你們實際操作的體驗。」
徒弟們紛紛發出「噢噢」的聲音,像是知識被扔進了他們的心中,發出的回響。大和尚最喜歡聽到這種反應了。這時,最機靈的小徒弟開口了,
「師父,所以說,要是搭配第一張圖,遮雨高度即會從原本的 w.tanθ 變成 w.secθ,各自可以再寫成\( \frac{w.sinθ}{cosθ} \) 和\( \frac{w}{cosθ} \),前者比後者多了 sinθ 倍,因為 sinθ 永遠小於1,所以當傘拿斜,永遠會比傘拿直的能遮住更多。」
「很好,你說的沒錯。」
大和尚滿意地點點頭。
「雖然數學是世間法,但有些時候,世間法也能幫助我們修行的。」
看著地上的圖,大和尚忽然轉身問最高的徒弟身高
「一米八四。」
「假設眼睛距離天靈蓋10公分,好吧,看來4.72公里以內,都還是沒有村莊了。」
他想起,好久以前,他曾經在附著了氣霧的玻璃上,這樣畫圖解釋數學,但那時候他還太年輕,不知道數學有這麼廣泛的應用。
註:更多賴以威的數學故事,請參考《超展開數學教室》。























-200x200.jpg)






