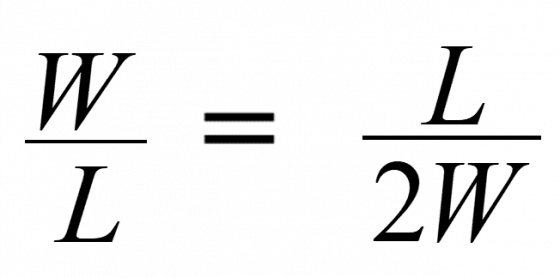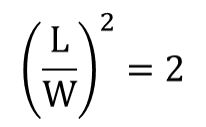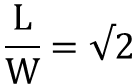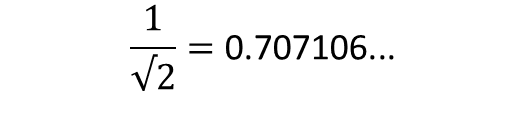站在巨人的肩膀上，看得比較遠

Photo Credit：rottnapples

“If I have seen further it is by standing on the shoulders of giants."

-Issac Newton

「如果說我看得比別人遠，那是因為我站在巨人的肩上。」

– 牛頓

說出這句話的牛頓，後來成了科學史上最偉大的巨人，比《進擊的巨人》漫畫裡能畫出來的巨人都還要大上許多，牛頓三大運動定律、微積分，無數的科學家與工程師站在他的肩膀上，發明出造福人類生活的技術。

不過，每次看到牛頓這句流傳千古的名言時，都會有一則回憶，從我內心深處彈出來。回憶裡的女孩那麼問著：「看得比較遠，是有多遠？」

※

我高中時還沒有101，台北市的頂點是台北火車站前的新光三越。當時，我們常說「約在新光三越的石獅子前面」。當時，手機只要能隨著來電時改變螢幕顏色，就是走在時尚與科技的最先端（如果你答出GD92，恭喜你至少跟我一樣老）。 當時，能跟暗戀的女孩子在周末補習後，拎著裝著補習班講義的紀念書包，用存了一周的零用錢買兩張到頂樓展望台的票，就是一個月、不，一學期以來最快樂的事情。

站在展望台的窗邊，行人小得像螞蟻、汽車小得像蟑螂（想到這裡，我打了個寒顫），整個台北盆地盡收眼底。下起雨，在地面是抬頭看雨滴從天而降，但在展望台上，是低頭看雨滴往地上撒。

「好漂亮的畫面噢。」

暗戀的對象這樣說，我在旁邊想說「再漂亮也沒你漂亮」，但想想拿人跟雨來比較好像不怎麼恰當，比雨漂亮這種讚美也應該讓人不知道該怎麼開心吧。這一猶豫，就錯過說話的時機了。

「如果沒有被盆地擋住，一直往外望，站在這麼高的地方看得比較遠，是有多遠呢？」暗戀的對象靠著窗邊說話。室內的冷氣很強，她的聲音停在牆上，化成一團霧氣。

我愣怔怔地站在一旁，只顧著忌妒那片玻璃，又想起小時候被同學罵過玻璃，到底罵人玻璃是什麼意思呢。耽溺於自己年少的過往，輕易錯過了一次在心上人面前表現的大好機會。

如果是現在，我會趕快結束妄想，挨近她身邊，在她造成的玻璃上的那團霧氣上畫一個大大的圓，圓上面畫兩個小人依偎在一起。當然，恐怕會因為畫太久，得叫她補呵幾口氣，別讓霧消失了。

接著，我會以小人為起點，畫一條與大圓相切的切線。

玻璃上的插畫示意圖

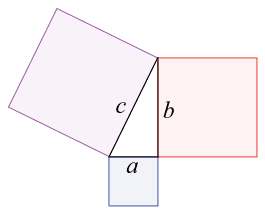
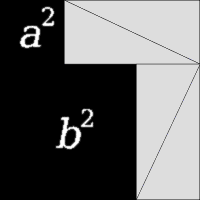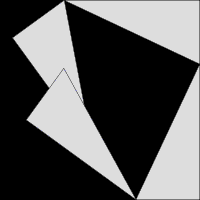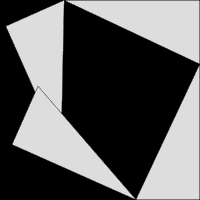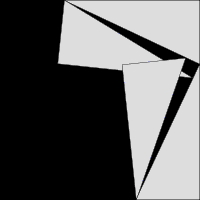
她一臉迷糊地看著我，我露出自信的微笑，告訴她：「這是地球，上面的兩個人，是站在新光三越頂樓上的我們。地球半徑約為 6400 公里，新光三越展望台高度為 250 公尺，利用畢氏定理，從我們所在位置畫出去的切線長度x為

(0.25+6,400) ²=6,400²+x²。

我俐落地列出一元二次方程式，但計算過程有點複雜，又不能要她連續呵氣，弄出一大面霧氣供我計算，畢竟是 250 公尺高的地方，這樣搞，她可能會缺氧吧!

不過這樣就可以作人工呼吸了也不錯……，不，我不能再妄想了！我趕緊化簡式子：

(0.250+6,400) ²=6,400²+x² 式子展開，

左邊是0.25²+2×0.25×6,400+6,400²，

第一項跟後面兩項比太小，可以忽略，第三項地球半徑平方又可以跟右邊第一項消掉，整理一下可得

x² 近似於2×0.25×6,400

x近似於根號√ (2×0.25×6,400)=56.6 公里。

也就是說，站在展望台的我們能看到 56.6 公里以外的景色。大概是宜蘭、還有東北角外海好幾公里的地方。」

她露出崇拜的眼神看著我，扯著我的袖子問我怎麼那麼聰明，要我教她數學。我裝作勉為其難，苦笑地答應，繼續若無其事地賣弄：

「先別說數學了，妳聽過『站在巨人的肩膀上，可以看得比較遠』這句話嗎？」

「嗯嗯，我記得是……」

「牛頓說的。」

她崇拜的眼神又增加了幾燭光。

方才的式子可以化簡成，看到的距離=根號(2H)×80公里，H是眼睛的高度，以公里為單位。如果要換算成以公尺為單位，要除以1000，變成

看到的距離=根號(20h)×0.8公里，這時h的單位就是公尺了。

換句話說，假設有一天我們去旅行。飛機失事在一片平坦的大草原上，倖存但走散的我們，在草原走來走去，尋找對方的蹤影。這時候，我比較有可能找得到妳。

「為什麼，說不定是我會先找到你啊。」

她賭氣地說

「因為我身高1.7公尺，眼睛位在1.6公尺的位置左右，而你的眼睛大概位在1.5公尺高。所以我們各自能看見的範圍大概是4.53公里和4.38公里左右，只要沒有障礙物，我看得可以比妳遠150公尺。我還是高中生，說不定我還會再長高到1.8公尺，那樣的話，我可以再多看130公尺。為，為了妳，我會長高的。」

「那答應我，你不能只是長高，還要練習跑步。」

「為什麼？」

「因為就算看到我了，我們之間的距離還有 4.53 公里。你要趕快跑過來接我……」

她說到最後，聲音越來越小，頭越來越低……我深深吐了一口氣，彷彿將肺裡所有的空氣吐出，走上前將她擁入懷裡，他的身體震了震，一股從曾體驗過的巨大喜悅從我心頭湧上。

「我不只是會早一點，遠遠地就會看到妳。我還希望從今以後，我都能看到妳所看見的一切，除了妳眼中的我，替換成我眼中的妳。」

※

那是我想出來最棒的告白台詞。嚴格來講，台詞有點問題，因為我們眼中的彼此左右還要對調。不過我想在那種情況下應該沒人會去認真追究這個細節。

可惜想出來時，三年已經過去了。

這三年間，我時常想起這段往事，在新光三越的我和她。想像裡的我每次都表現得更好，更能打動想像裡的她的心。奈何現實之中，不管是她、我的身高、或我的跑步，都失敗了。要是能早點站在巨人的肩膀上，早點懂得將數學應用在生活當中，或許就不會是這樣的結局了。

註：更多賴以威的數學故事，請參考《超展開數學教室》。

泛科學總編輯鄭國威招牌課程再度開課，面對面傳授閱讀理解、科普寫作到內容行銷的心法，幫助你打造個人品牌。

慶祝泛科學院周年慶，快來領取專屬優惠，現在購買課程還有機會抽中 $1,111 折價券喔！課程傳送門請點我