只要知道黑洞的質量和自旋速率,我們就能從愛因斯坦的相對論定律推導出它的其他特性:大小、重力的引力強度、它的事件視界受離心力影響在赤道附近向外伸展多遠,以及它的重力透鏡效應如何影響其背後的星體。一切的一切。
這實在非常神奇,跟我們的日常經驗是那麼不同。
這就好比只要知道我的體重,還有我能跑多快,就能夠推導出關於我的一切:我的眼珠是什麼顏色、鼻子有多長、智商有多高⋯⋯我的恩師惠勒─創造「黑洞」這個名稱的人─用「黑洞沒有毛」這句話來描述這一點:黑洞它別無其他獨立特性,除了質量和自旋之外。
所以,其實他應該說「黑洞只有兩根毛,而你可以從這兩根毛推導出關於它的一切」才對。但這句話實在不如「沒有毛」那麼順口,於是「沒有毛」這個用詞很快在黑洞這門學問和科學家的語彙中生根。
從《星際效應》片中所述米勒的星球所屬特性,懂得愛因斯坦相對論定律的物理學家,就能推導出「巨人」的質量和自旋,從而得知有關那個黑洞的其他所有特質。讓我們看看這是怎樣辦到的。
「巨人」的質量
我們會知道這一點,是因為庫柏一行人在這裡損失極大量的時間,這只有在非常靠近「巨人」的地方才可能發生。
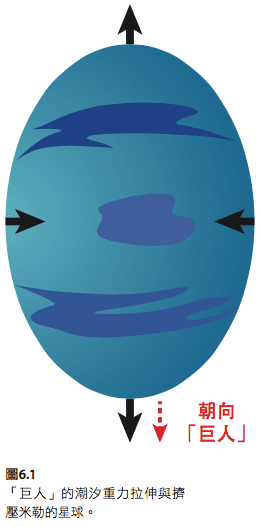
在那麼近的距離下,「巨人」的潮汐重力作用(第四章)會特別強大。它拉扯著米勒的星球朝向與遠離「巨人」,並擠壓星球的側邊(圖6.1)。
這種拉伸和擠壓的力道,與「巨人」質量的平方成反比。為什麼?
當「巨人」的質量愈大,它的圓周也愈長,於是「巨人」作用於米勒星球各不同部位的重力強度也會比較相近,而這麼一來,潮汐力就會比較弱(見牛頓對潮汐力的觀點;圖4.8)。
經過許多精密的運算後,我推斷出:「巨人」的質量至少必須達到太陽質量的一億倍。「巨人」的質量若低於這個數值,它就會撕裂米勒的星球!
我在《星際效應》一片中提出的科學詮釋,全都是假設「巨人」的質量就是這麼大:相當於一億顆太陽。
比方說,第十七章談到「巨人」的潮汐力時,我就是設定它具有這種質量,據此說明它如何在米勒的星球上掀起滔天巨浪,向「漫遊者號」撲來。
黑洞事件視界的周長,與黑洞的質量成正比。以「巨人」相當於一億顆太陽的質量來計算,可得出視界的周長大約相當於地球的繞日軌道:十億公里左右。真的很大!
富蘭克林的視覺特效團隊和我商議後,採用了這個周長來打造《星際效應》片中的影像。
物理學家認為黑洞的半徑等於其視界周長除以2π( 約6.28)。由於黑洞的內部有極高度的翹曲現象,所以那並非黑洞的真正半徑─不是在我們這處宇宙中所測得的從視界到黑洞中心的真正距離,而是在「體」之中測得的事件視界半徑;見圖6.3 的下部。
在這種意義下,「巨人」的半徑約為一億五千萬公里,相當於地球繞日軌道的半徑。
「巨人」的自旋
當克里斯多福.諾蘭告訴我,他希望時間在米勒的星球上減速多少─他要那裡的一個小時等於老家地球上的七年─我聽了後整個傻眼。我覺得那是不可能的,所以我告訴克里斯多福辦不到。
但他堅決地表示:「沒有商量餘地。」於是我只能回家埋頭苦思(這不是頭一遭,也不是最後一次),用愛因斯坦的相對論方程式算了又算,終於想出一個辦法。
我發現,假如米勒的星球和「巨人」之間相隔的距離,約等於不會讓它墜入黑洞的最近距離,16 加上如果「巨人」自旋的速度夠快,則克里斯多福的「一小時等於七年」的時間減速作用是有可能辦到的。但「巨人」的轉速必須非常非常快。
黑洞的自旋速率有一個最大值。當自旋速率高於這個最大值,它的視界就會消失,使整個宇宙都看得到它裡面的奇異點;意思是,它整個裸露在外,一無遮掩─這恐怕不是物理定律所能容許的事(第二十六章)。
我發現,想達到克里斯多福的時間極度減速要求,「巨人」的轉速就必須逼近最大值,只比最大值低約百兆分之一。我在《星際效應》片中所做的科學詮釋,大多採用這個自旋速率。
當機器人塔斯墜入「巨人」時(圖6.2),18「永續號」的成員可以從非常、非常遙遠的地方直接觀測「巨人」的自旋速率。
從遠處看去,塔斯始終沒有跨入視界(因為當它跨入其中後,就無法把信號傳出黑洞)。事實上,塔斯的墜落速度看起來整個慢了下來,而且好像盤旋在視界的正上方一樣。當塔斯在盤旋時,從遠處看去,它也被捲進「巨人」的旋動空間,繞著「巨人」一圈圈打轉。而由於「巨人」的自旋速度非常接近可能的最大值,因此從遠處看去,塔斯的軌道周期約為一個小時。
你可以自己動手計算一下:環繞「巨人」運行的軌道距離為十億公里,塔斯只花一個小時就跨越那段距離,所以,從遠處測定的結果,塔斯的速度約為每小時十億公里,這已經接近光速了!
倘若「巨人」自旋速率高於最大值,塔斯就會快馬加鞭以超光速繞行黑洞,而這違反了愛因斯坦的速度限制。這樣思考下來,你就會明白為什麼黑洞的自旋速率要有一個可能的最大值。
我在一九七五年發現了一種大自然藉此防範黑洞自旋速率超過最大值的機制:當黑洞的自旋速率接近最大值時,它很難再捕獲繞軌方向與黑洞本身旋轉方向相同的物體,否則該物體一旦被捕獲,就會提高黑洞的自旋轉速。
但黑洞可以輕易捕獲繞軌方向與黑洞本身旋轉方向相反的物體,而該物體一旦被捕獲,就會減緩黑洞的自旋轉速。所以,當黑洞自旋速率接近最大值時,會很容易減緩下來。
我的這個發現,重點在討論一種盤狀氣體構造,有點像是土星環,而且和黑洞自旋以同方向繞軌運行。它叫做吸積盤(accretiondisk,第九章)。
吸積盤內的摩擦力,會導致氣體逐漸螺旋墜入黑洞中,並提高其轉速。摩擦還會使氣體升溫,使之放射出光子。黑洞周圍的空間旋轉作用會抓住與黑洞自旋同向行進的光子,將它們向外甩去,於是光子進不了黑洞。
相對地,空間旋轉也會抓住試圖與自旋反向行進的光子,將它們吸進黑洞,從而減緩自旋轉速。最後,當黑洞自旋達到最大值的0.998 倍時,就會達到一種均勢,這時候,被捕獲光子所造成的減速作用,正好抵銷了吸積氣體造成的加速作用。這種均勢看來還算穩健。就大多數天文物理環境來說,我認為黑洞的自旋都不會比最大值的0.998 倍左右還快。
但我可以想像在某些情況下─非常罕見,或永遠不會出現在真實宇宙,只是仍然有可能性─自旋可以極逼近這個最大值,甚至逼近到可以讓時間在米勒的星球上減速、達到克里斯多福的要求:比速率最大值只低了百兆分之一的自旋─這雖然不太可能,卻還是有可能。
要拍出好電影,高明的電影人經常得把事情推到極致。這在電影界是司空見慣的事。就《哈利波特》這類科學奇幻片來說,它的極致狀況遠遠踰越了科學可能性的邊界。至於科幻片的極致狀況,則一般都約束在可能性的範疇之內。
這就是科學奇幻片和科幻片的主要區別。《星際效應》是一部科幻片,不是科學奇幻片。「巨人」的最高自旋轉速,在科學上是有可能成真的。
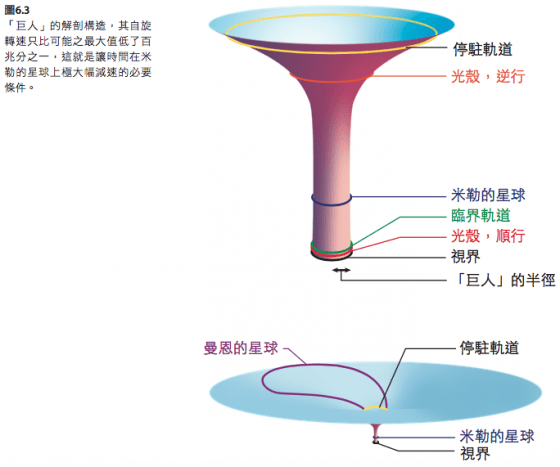
「巨人」的解剖構造
決定「巨人」的質量和自旋速率之後,我再用愛因斯坦的方程式估算出它的構造。就像前一章的做法一樣,這裡我們只先專心討論外部構造,內部(尤其是「巨人」的奇異點)就留待第二十六和二十八章再討論。
圖6.3 的上半圖,顯示從「體」審視「巨人」赤道面時所見的形狀。它和圖5.5 非常相像,只是由於「巨人」的自旋轉速遠遠更為逼近可能之最大值(百兆分之一相對於圖5.5 的千分之二),因此「巨人」的咽喉也長了更多,向下延伸很大的長度才觸及視界。從「體」觀察它,視界附近看來就像個長形圓柱。圓柱形部份的長度,約兩倍於視界的周長,也就是二十億公里。
圖中的圓柱的截面都呈圓形,不過倘若我們移動脫離「巨人」的赤道面,恢復我們的「膜」的第三次元,那些截面就會變成壓扁的球面(球狀體)。
我在「巨人」的赤道面上標出好幾個特殊位置,它們全都含括在我對《星際效應》的科學詮釋之中,諸如:
- 黑圈:「巨人」的事件視界;
- 綠圈:臨界軌道─電影接近尾聲時,庫柏和塔斯就是從這裡墜入「巨人」(第二十七章);
- 藍圈:「米勒的星球」的軌道(第十七章);
- 黃圈:停駐軌道─庫柏一行人探訪米勒的星球時,「永續號」停駐在此;
- 紫圈:「曼恩的星球」從非赤道面突伸進入「巨人」赤道面的片段軌道。
在這當中,由於「曼恩的星球」軌道的外側部份偏離「巨人」極遠(約相當於「巨人」半徑的六百倍或更遠;第十九章),因此我必須用大上許多的比例尺再另外畫一張圖來表現它(圖6.3 的下半圖),但儘管我已經這麼做了,還是沒有據實將它畫出來。我把它的外側部份畫在只跟「巨人」相隔一百倍半徑距離的位置上,事實上應該相隔六百倍半徑才對。
除了上述細節之外,還有一個紅圈,我標示為「光殼」,意指「火光殼層」(shell of fire, Sof);詳情請見下文。
我是怎麼決定這些位置的?這裡我先舉停駐軌道為例,之後再討論其他的位置。
庫柏在電影裡是這樣描述這個停駐軌道:「所以我們進入『巨人』一條比較大圈的軌道,跟米勒的星球平行,只是稍微偏外側一些。」他還希望這個停駐軌道能和「巨人」保持充分的距離,這樣才能「避開時間偏移」,意思是,和「巨人」保持一段「時間減速作用不會與地球時間相差過大」的距離。
這促使我最後選定「巨人」五倍半徑的距離(圖6.3 下半圖的黃圈)。「漫遊者號」從這條停駐軌道航向米勒的星球得花兩個半小時─這一點,也強化了我這個決定。
但是這個決定有個問題。在這個距離之下,「巨人」會看起來非常龐大;它會跨越「永續號」約五十度的天空。那景象,簡直令人歎為觀止。但這樣有氣魄的場景太早出現在電影裡─這可不是大家樂見的!於是克里斯多福和保羅決定,從停駐軌道看到的「巨人」尺寸必須大幅縮小,從五十度變成約兩度半,相當於我們從地球看月球所見尺寸的五倍大小─仍然相當可觀,但不至於大到嚇人。
光殼
「巨人」的附近,重力非常強大,空間和時間也翹曲得非常厲害,導致光線(光子)有可能被困在視界外側的軌道上,不斷環繞黑洞無數圈之後才逃逸散去。
這麼看來,視界外側的軌道其實是不穩定的,因為最後光子終究會逃逸。(相對地,視界內側被捕獲的光子就永遠出不來了)我習慣把這種短暫「受困」的光稱為「火光殼層」,簡稱「光殼」。它在構成《星際效應》片中「巨人」視覺外觀基礎的電腦模擬作業(第八章)上扮演非常重要的角色。
就不自旋黑洞來說,光殼是個球面,周長為視界周長的一.五倍。受困的光線在這個球面上,順著大圓(就像我們的地表恆定經線)一圈圈繞行;當中有些逸入黑洞中,其餘的向外流洩,遠離黑洞。當黑洞加速自旋,光殼也同時分別朝內、外擴展,從而擁有了一定的體積,而不只是一個球體的表面而已。
以「巨人」來說,由於它的自旋速率極高,赤道面的光殼於是從圖6.3 的底部紅圈,擴展到上方紅圈,規模大到連米勒的星球和臨界軌道都含括在內,甚至比這還更大更遠!
圖6.3 底部的紅圈是順著「巨人」自旋方向(順行)、一圈圈繞行「巨人」的一道光線(光子軌道),上方的紅圈則是與「巨人」自旋方向逆向運行(逆行)的光子軌道。很顯然的,空間旋動使順行光線與視界貼得很近─逆行光線則沒那麼靠近─又不至於落入黑洞。
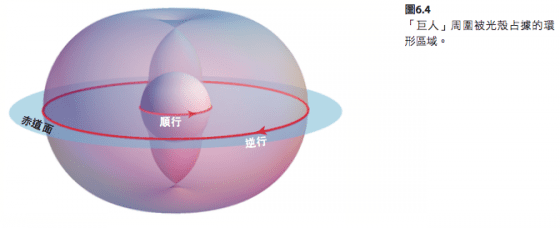
由此可見,空間旋動的影響是多麼巨大!赤道面上、下空間被光殼占據的範圍,如圖6.4 所示。這是一個很大的環形區域。這幅插圖省略了空間翹曲現象,因為呈現空間翹曲就無法畫出光殼完整的三個次元。
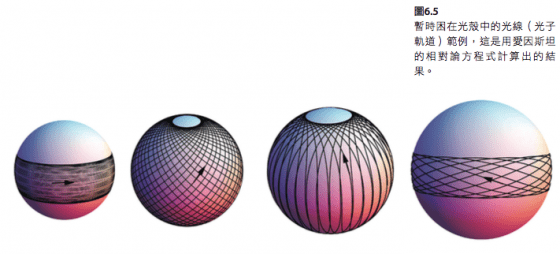
圖6.5 所示為暫時困在光殼中的光線(光子軌道)之幾個範例。黑洞就位於這些軌道的中央。最左側的軌道盤繞著一個較小球體的赤道區域,始終與「巨人」的自旋同向順行。它和圖6.3 底部與圖6.4 內側的紅圈幾乎完全相同。
圖6.5 中,左邊第二條軌道則環繞著一個稍大球體,行進方向接近兩極並稍微偏順行。第三條軌道的環繞範圍還更大,但方向為逆行,並接近兩極。第四條軌道非常貼近赤道並逆向行進,亦即與圖6.3 上方與6.4外側的紅色赤道軌道相似。
這些軌道其實是彼此相互交疊的,這裡我將它們拆開來描繪以便檢視。
暫時困在光殼中的光子有些會向外逸出,螺旋行進脫離「巨人」黑洞;其餘的光子則向內螺旋行進逃向「巨人」,一頭栽入視界中。
那些險些受困但成功脫逃的光子,對《星際效應》片中「巨人」的視覺外觀有非常重大的影響:它們勾勒出「永續號」隊員眼中所見的「巨人」陰影邊緣,並在陰影邊緣製造了一道明亮的細線:「火環」(ring of fire)─我們在第八章會談到它。