- 作者/蔣維倫|泛科學 PanSci 專欄作家、故事專欄作家、udn 鳴人堂專欄作家、前國衛院衛生福利政策研究學者。喜歡虎斑、橘子、白底虎斑和三花貓。
Take Home Message
- 近視是因為角膜或眼球變形,使眼球折射光線能力太強,焦點落在視網膜前方,所以無法獲得清楚的景象。
- 雷射治療近視以達到減弱折射力為目的,主流術式有雷射原位層狀角膜塑型術(LASIK)和微創角膜透鏡提取術(SMILE)。
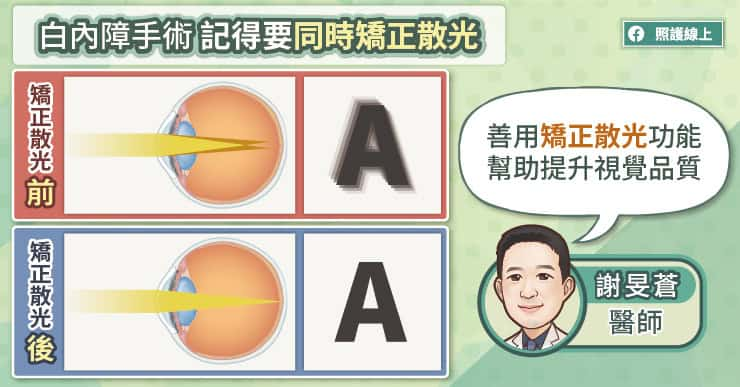
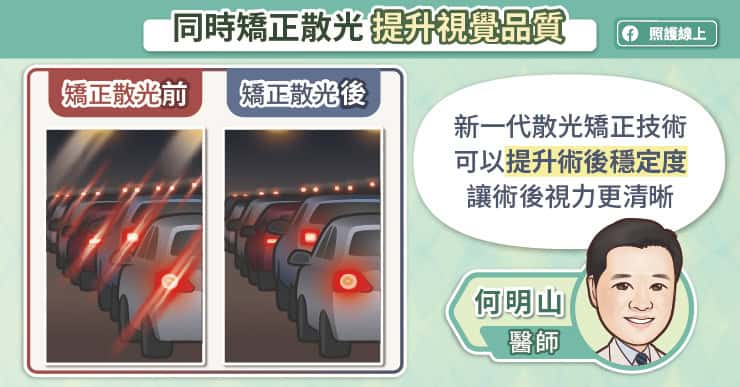
- 經雷射手術後,患者視力可以回到配戴眼鏡前的水準,散光減輕到輕度散光。不過術後最常見的副作用是乾眼症,因此手術前需和專業醫護團隊討論。
你常覺得遠處的景物看不清楚,總是要瞇著眼看東西嗎?這些都是近視的典型症狀。近視通常在 6~14 歲之間出現,多數人於 20 歲後趨向穩定。目前尚未釐清近視出現的原因,但戶外活動時間較長的兒童,近視的風險較低,不過仍不清楚是因為「看比較遠」、「戶外光線」,或「運動量較高」等因素所致。全世界的近視盛行率非常高,在美國,超過四成的人罹患近視,而東亞的一些國家,如臺灣,兒童的近視率甚至達八成以上。
壞掉的攝影機
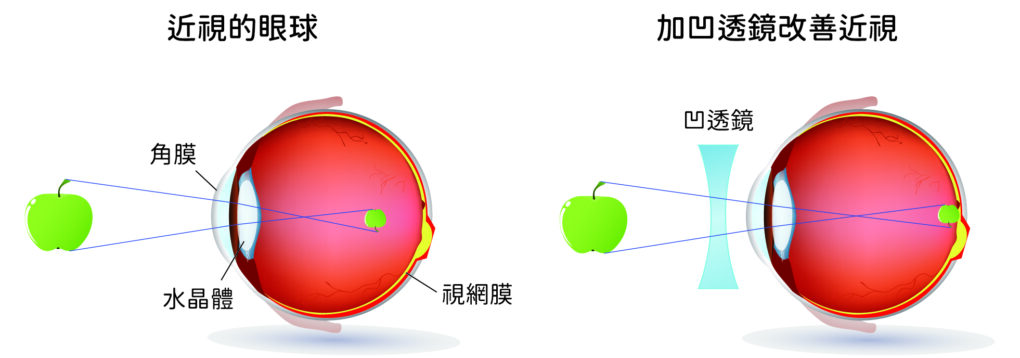
為什麼會近視?主要是因為眼睛的結構是透過「折射光線、將光聚焦在眼底的視網膜」來獲得清晰的投影輪廓。所以當眼球變形(變扁)或角膜折射光線能力有問題(形狀出錯)時,光線聚焦的焦點會落在視網膜前方(圖一),投影在視網膜時就會呈現模糊的輪廓,無法獲得清楚的景象,此時稱為近視。當你的近視度數愈深,焦點就會距離視網膜愈遠。因此最簡單的改善方式,就是加一塊凹透鏡(眼鏡)來發散光線,進而調整光的路徑,讓光線重新聚焦在視網膜上。
切掉一點眼睛如何?雷射治療近視的原理
既然近視是「眼球折射光線的能力太強」,那麼用刀削掉一點眼睛,這樣可行嗎?可以。
如前所述,近視是由於眼球變形或折射力太強,使光線焦點落在視網膜之前。目前無法矯正變形的眼球,因此調整光線折射路徑,就成了最佳的治療方式。而眼球負責折射光線的組織,為最前方的角膜和位置在後方些的水晶體(圖一);而又因為角膜暴露在外,醫師能用刀械直接削除,或是雕塑外型,所以角膜組織就成了外科手術治療近視的最直接選擇。雖然調整水晶體也能改善近視,但較不普遍。
最早,醫生便是利用刀具削去角膜以治療近視。 但需注意,削去眼球結構減弱聚焦能力,進而改善近視,仍不算是「治療」。由於這個方法無法改變眼球的整體形狀,因此眼球變形後,造成視網膜剝離等疾病的風險仍存在。
在雷射技術發明之前,醫師會用層狀角膜重塑術(automated lamellar keratoplasty , ALK)——微型刀械移除角膜組織,達到減弱折射力的目的,這種手術方式約盛行於 1980~1990 年代。直到雷射技術成熟後,才開始應用於治療近視,雷射依原理和發展時程可分為雷射屈光角膜切除術(photorefractive keratectomy , PRK)、雷射原位層狀角膜塑型術(laser-assisted in-situ keratomileusis , LASIK)、微創角膜透鏡提取術(small incision lenticule extraction , SMILE)。
雷射屈光角膜切除術(PRK)
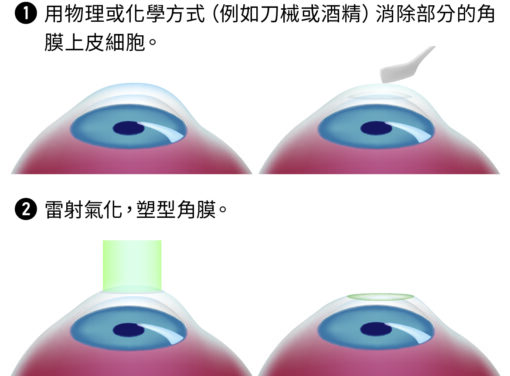
雷射於 1980 年代開始用於治療近視,並逐漸發展出 PRK 術式。PRK 原理是利用雷射能固定能量的焦點、升高局部組織的溫度、進而氣化掉部分角膜最外層的上皮層細胞(epithelium,圖二),達到減少角膜厚度、降低折射力的目的(圖三)。
在此技術問世後,PRK 迅速地成為治療近視的首選,但因為要削掉角膜上皮層,同時也氣化了角膜裡的痛、觸覺神經,容易導致術後劇烈疼痛和視力恢復期過長等問題;再加上大面積的傷口直接暴露在外,術後洗頭、洗臉也容易導致感染,所以在新技術出現後,選用 PRK 的患者也逐漸減少。
雷射原位層狀角膜塑型術(LASIK)
LASIK 為目前雷射治療近視的主要術式之一。為了要減少 PRK 術後疼痛且感染風險高的困擾,科學家思考,是否能改善術式,盡可能地減少暴露在外的傷口呢?在 1990 年代,醫師開始建構另一種術式,也就是現在常聽到的 LASIK。
它所氣化的部分和 PRK 不同,主要是削除角膜裡的基質層(stroma)、盡可能地保留上皮層組織完整性;手術先切出一個類似「C」的傷口、創造並掀開一片角瓣膜(corneal flap),然後以雷射直接氣化、雕塑基質層細胞後再將角瓣膜覆蓋住傷口(圖四)。和 PRK 相比,LASIK 較少暴露於外界的傷口,感染風險較低。
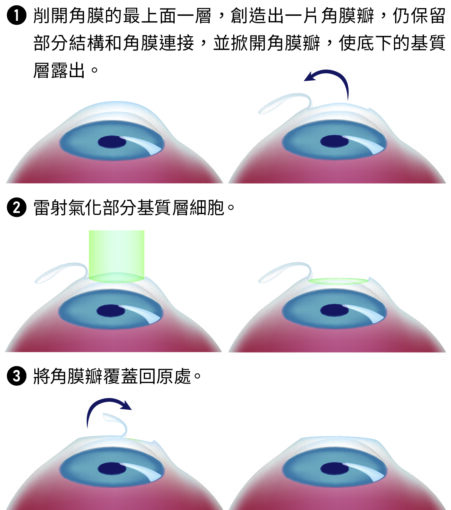
由於術後恢復期較短且傷口較不會感到疼痛,使 LASIK 逐漸取代 PRK,成為主流術式之一,目前接受 LASIK 的眼球超過數百萬顆以上。
微創角膜透鏡提取術(SMILE)
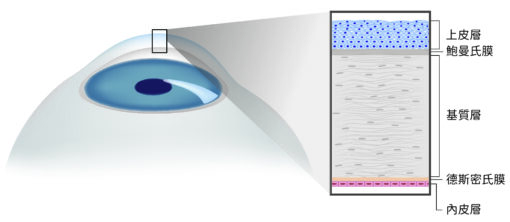
為什麼要一直改良手術?因為醫學界希望能減少破壞角膜神經、縮小暴露外界的傷口。角膜是布滿神經的組織,能感受細微異物、刺激淚水分泌,達到排除異物、潤滑眼球的功能。神經束從內而外伸出、穿出鮑曼氏膜(Bowman’s membrane)並彎曲近直角、在上皮層細胞和鮑曼氏膜之間形成豐富的神經末梢(圖二)。
從角膜神經的分布可以推測出,最早的 PRK 氣化上皮層細胞的缺點,就是削除了神經末梢,造成傷口大面積的暴露,進而導致術後疼痛。而 LASIK 雖然減少了傷口暴露,但由於切出「C」形狀傷口、創造角膜瓣時,也同時切除了大部分的神經,導致大規模的神經受損,進而使眼睛無法自主分泌淚水,引起嚴重的乾眼症。所以科學家持續地構思新的解決方法。
相較於前兩種術式,SMILE 的歷史最短,它起源於 2002 年德國團隊的想法,直到 2007 年才開始臨床試驗。幾年後術式逐漸成熟,在 2016 年獲得美國許可治療近視,僅一年時間,全球就累積超過 100 萬次手術。
SMILE 使用雷射「可在特定深度聚焦」的優勢,手術分成兩個步驟:首先,聚焦雷射,隔空在角膜的基質層裡切出一個極小的凸透鏡結構;接著,在角膜表面切出約三毫米(mm)的小傷口,取出小透鏡。與 LASIK 須開出「C」形狀的傷口、斷開大部分的神經相比,SMILE 的創口較小,理論上切斷的神經比例較少、乾眼症的機率也較低,所以快速地成為患者主要選擇的術式之一。
雖然 SMILE 為較新的技術,但不能就此認定 SMILE 比 LASIK 更優秀。醫療手術仍須視個人體質、需求、經濟能力等,進行專業的個人考量。
雷射以後,連打靶都比較準了
許多人的工作高度仰賴視覺,軍人就是其中之一。在美國,SMILE 可治療近視和散光。去(2021)年《白內障與屈光手術期刊》(Journal of Cataract & Refractive Surgery)刊出一篇論文,研究 37 名軍人(74 顆眼睛)在 SMILE 術後的短期視力改變 。術前,患者皆有輕至中度的近視或散光,且分別有 10% 和 20% 的患者反應近視困擾了他們的工作和生活狀態。
而在 SMILE 術後的三個月內,約 96% 的眼睛在不戴眼鏡(裸視)的情況下,視力可以達到正常人的標準[註]。而原先生活和工作受到視力問題困擾的患者,全都降為 0%。在感受度調查也發現,約 83% 患者對手術後擁有的視力更加滿意。其中 14 名軍人在手術前後都接受槍法打靶測試,儘管統計結果並無顯示出差異,但手術後的打靶成績稍稍高了些。不過,仍不能認為雷射近視手術使槍法更精準。
[註]正常視力的標準為裸視遠視力(uncorrected distance visual acuity , UDVA),意思是在史奈侖(Snellen)視力表裡,能看到 20/20(對應視力約 1.0)或更小的字。
手術的功效可以維持多久?
中國上海復旦大學附屬眼耳鼻喉醫院,發表了一系列長期的研究,追蹤接受 SMILE 手術後的患者多年,並討論他們的視力改善。團隊招募了 26 人(26 顆眼睛,皆為單眼接受手術),接受 SMILE 約七年或更久。發現 26 顆眼睛在術後七年的視力,比七年前戴眼鏡時更好!以史奈侖視力表上 20/20 的字母為標準,術前 96% 的眼睛戴眼鏡時可看清楚,術後有 100% 的眼睛在裸視或脫離眼鏡後可看清楚。
而視力表裡更小的一行字(20/16,對應視力約 1.2),術前有 38% 的眼睛戴眼鏡時可看清楚,術後有 73% 的眼睛在裸視或脫離眼鏡後可看清楚。再小一行的字(20/12.5,對應視力約 1.6),有 19% 的眼睛在雷射手術後可辨識清楚;而手術前,所有的眼睛在戴眼鏡後,都無法看清該行字。
換言之,經過近視雷射手術後的患者不僅擺脫了眼鏡,視力還可回到或優於配戴眼鏡前的水準;在散光方面,所有人在術前都有輕至中度不等的散光,而手術七年後,幾乎所有人都減輕為輕度散光。
雷射後會有後遺症嗎?
任何醫療手術都會有副作用,SMILE 最常見的術後副作用是乾眼症。儘管多個研究都認為,SMILE 的乾眼症比例及嚴重度都比 LASIK 少,因為和 LASIK 相比,SMILE 的優勢是創口較小且切斷的神經較少,因此術後保有較多神經,眼睛控制淚腺的能力較佳,乾眼症也較輕微,且恢復期較短。但這不代表不會出現乾眼症,和未接受手術的眼睛相比,SMILE 後眼睛分泌的淚水仍可能比較少。因此術後的自我照護,例如短期內避免感染和定時且長期地使用人工淚液,是雷射治療近視的必要作業。
儘管 SMILE 是安全的手術,且全球已有百萬例手術的經驗,但仍可能有手術中途失誤的情況發生,例如移除雷射切除的部分時,仍有殘存組織遺留在角膜內,或是失誤而切穿角膜上皮組織等。根據統計結果,這些手術中途失誤的發生率總和小於 1%,且似乎和醫護團隊的學習曲線有關,可能新手醫師比較容易發生手術中途失誤。不過,SMILE 令人最有感的副作用應該是金額,價格在十萬以上,並不是能輕鬆負擔的數字。


- 〈本文選自《科學月刊》2022 年 5 月號〉
- 科學月刊/在一個資訊不值錢的時代中,試圖緊握那知識餘溫外,也不忘科學事實和自由價值至上的科普雜誌。