「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2019數感盃青少年寫作競賽 / 高中職組專題報導類銀獎 之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
- 作者:權嘉、謝念彤/慈大附中

「好奇心是科學工作者產生無窮的毅力和耐心的源泉。」—愛因斯坦
近幾年來,以「時空變換」為題材的電影,愈加吸引觀衆的眼球。這些結合科幻、驚悚、懸疑、燒腦為一體的視覺盛宴,主角往往在超越時空的過程中,因為種種不可預知的原因下,無法順利重返自己的家園。他們會想盡一切辦法,結合自己所學的知識,嘗試避免事故再度發生。但螢幕前的我們只能提心吊膽的牽掛著主角未卜的命運,靜靜的守候後續的發展,其他都無濟於事。
2018 年 10 月 21 日下午四時五十分,臺鐵 6432 次普悠瑪自强號列車在新馬車站旁發生火車脫軌事故,全車 366 人,18 人死亡,215 人輕重傷,震驚社會大衆。此次發生事故的臺鐵 TEMU2000 型電聯車是投入營運以來第一次發生如此嚴重的死傷,所有人的目光都關注著事故原因的調查結果,作為高中生的我們也不例外。我們多麽想超越時空,幫他們「度」過回家的路啊。
隨著新聞媒體雜七雜八的報導,獲取的大量資訊也引起我們的好奇。「列車過彎超速」、「新馬站彎道過急」、「列車ATP關閉」、「350度大彎道!」、「超速140km/hr」……我們注意到諸多的討論聲浪都有它們共同的特點,沒有數據作為依據,或是利用數據危言聳聽的嫌疑。於是我們想要查詢出相關參數,結合在學校學習的知識,用數字説話,找出答案。
根據行政院事故調查小組公佈的結果顯示,列車超速過彎是導致脫軌的原因之一。6432 次普悠瑪列車過彎速度高達 140km/h,過彎並未減速,遠超過新馬站過彎速限 70~85km/h。可是根據車輛參數,TEMU2000型電聯車的設計最高速度是 150km/h,營運最高速度是 130km/h,明明在合理的速限內,為什麼要在新馬站過彎限速呢?
經過進一步查找資料,我們發現過彎限速與新馬站 306「度」的彎道有關,而這個 306「度」是鐵道的曲線半徑,也就是指鐵道的彎曲程度。新馬站的306「度」軌道是全台灣最彎的路段之一,所以列車經過時需要限速,就像開車過彎時需要減速一樣。下圖是台灣鐵路局-列車曲線運轉速度表,傾斜式列車通過曲線半徑 306 公尺的彎道安全速度為 85km/h,所以事發列車若超過限速確實會有不安全的隱憂。
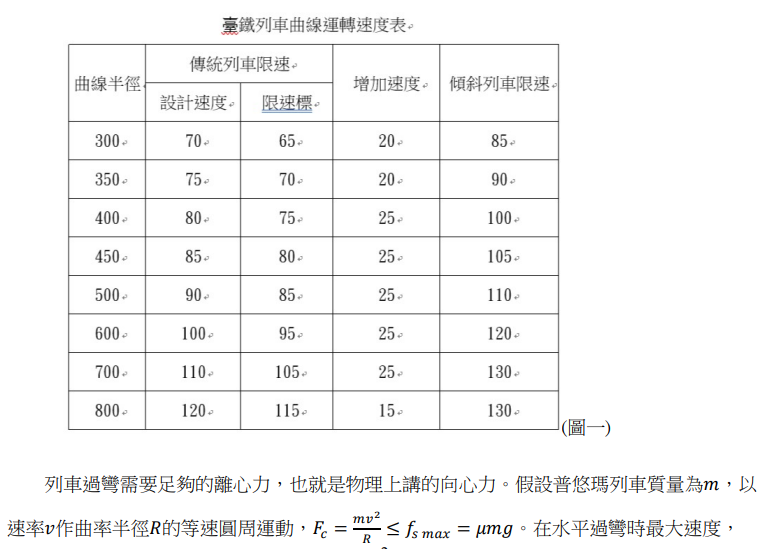


表格中的黏著係數指機車動輪不空轉時的最大輪周牽引力與黏著重量的比值﹐也就是摩擦係數。因為我們不瞭解事發鋼軌是否做撒砂處理,東部地區環境又潮濕,故採用三種情況分別計算。
而當時的火車時速又是多少,才導致了火車的翻覆?根據已知的資料,台鐵表示當時列車是以 140km/hr 進入半徑 306 公尺的新馬站彎道,但司機卻說當時控制車速在 82、83 公里,雙方說詞不同,而事後台鐵員工也表示當時數位時速顯示 57 公里,但 ATP 卻顯示 100公里,各方表示的時速都不盡相同,到底正確的時速是多少呢?於是,我們利用影格分析事發時的監控錄像來計算普悠瑪事發時速,計算方法以火車全長(含車頭 22095mm、車尾20700mm)
經過參照物柱子的時間差來計算。已知參數如下:
總車長:22096𝑚𝑚 × 2 + 20700𝑚𝑚 + 6 = 168390𝑚𝑚
車頭過第一根柱子時間:1”23
車尾過第一根柱子時間:6”21
經過時間 :4”28 → 4.9 秒
168390 ÷ 4.9 × 3600 = 123.7𝑘m/ℎ𝑟
經過影格分析,我們算出的事發列車通過時速是 123.7km/hr,並未到 140km/hr。雖然有影片畫質和影格截取等外在影響因素,也會有少許的誤差。但和台鐵公布的 140km/hr,還有司機方面的 82、83km/hr 都有明顯的落差。孰是孰非,無人知曉。而且,時速 123.7km/hr也遠超過官方規定新馬站過彎速限70~85𝑘m/ℎ𝑟。
這讓我們想到 2005 年 4 月 25 日,日本也發生過和台灣一樣的翻車事件。因為火車誤點了 1 分 20 秒,司機為了避免「JR 西日本」的誤點處分,以時速 116km/hr 經過曲率半徑 304 公尺的彎道,而此路段的安全限速是 70km/hr,因此而翻車。但據瞭解,原本這段道路並不是如此彎曲,而是在 1997 年時,JR 為了縮短至尼崎的行車耗時,在塚口以南貨物站的改建工程中,將曲率半徑由原本較緩和的 600 公尺改建較彎曲的 304 公尺,所以才會和新馬站一樣有過彎限速。
但台灣的鐵路也不只有新馬站需要過彎限速,在瑞芳-猴硐路段、八堵-四腳亭路段、南靖-後壁路段,曲線半徑都有 300~400 公尺。以普悠瑪來說,限速也都在 85 公里,都是有危險性的。可見,彎道對高速列車的影響是很大的。
除了彎道對高速列車會有很大的影響,列車的傾斜角度也是會有影響的。經過查詢交通部鐵路工程局的資料,臺鐵採用 1067mm(窄軌)軌距,軌道外軌超高上限為 105mm.我們假設軌道外軌超高傾斜角為 θ,可以得出:
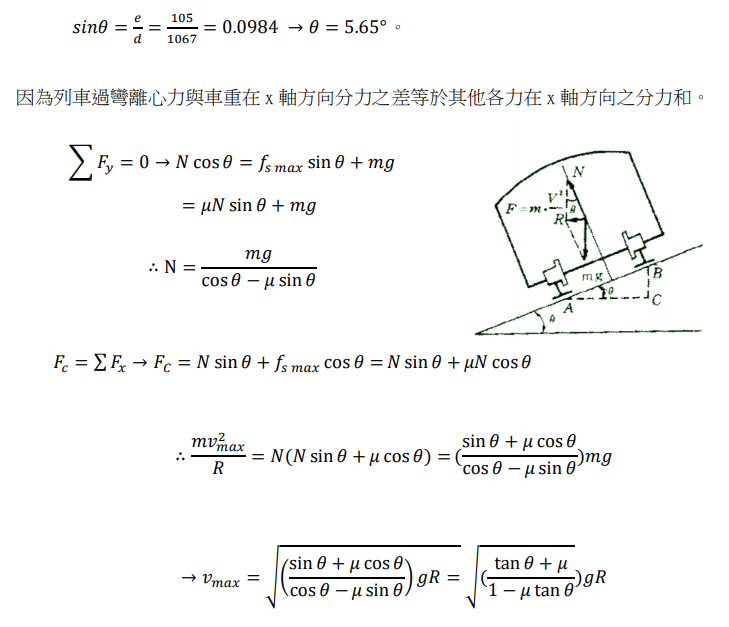

倘若沒有其他外在因素,根據以上數據我們可以知道,即使普悠瑪列車未依照限速規定通過彎道,只要列車時速控制在 112.41km/hr 以下,都可以安全通過。
存在物就像是奔騰不息的河流,事物處於不斷變化之中。—馬可·奧勒利烏斯:《沉思集》
在不同的軌道面黏著係數和傾斜角的情況下,列車最大過彎時速:
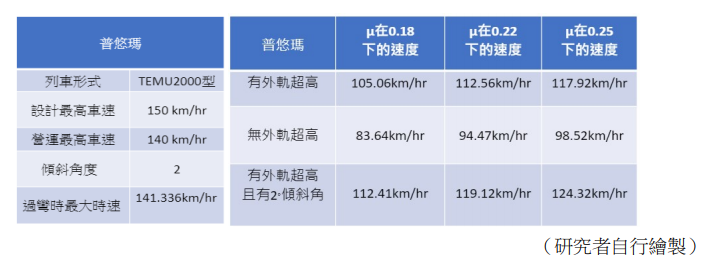
表格中普悠瑪列車在新馬站彎道不同軌道面黏著係數、不同軌道傾斜角的數據環境下,計算得出的過彎最大時速都稍大於臺鐵營運限制最高時速。這些速度差可能來源於軌道壽命、乘車舒適度、輪緣傾斜角等其他外在因素。
「學問是解決問題的,而且真的學問是解決自己的問題的。」—梁漱溟《出世入世》
經過研究普悠瑪事件,我們意外發現儘管生活在資訊科技發達的社會,想要取得正確的資訊仍然是一波三折,且還會推諉責任。例如:人民對政府掌握的公共領域的資訊,並非垂手可得,甚至無解!同時我們發現數字的背後隱藏著不可告人的秘密,以致媒體斷章取義、做出誇張不實的報導。這時我們就需要有敏銳的判斷力和對數字的敏感性,不能人云亦云。
我們在探究的過程中,釐清了媒體對於彎道曲率半徑的概念混淆,也用數字解答了我們的疑惑。通過計算水平過彎和傾斜過彎的速度極值瞭解設置外軌超高提高行車效率的意義。思考臺鐵新馬站彎道的限速和利用影格分析出的列車事發速度,對比我們模擬計算的理論最大安全速度,得出結果: (一)我們利用影格分析的事發車速數據高於理論最大安全速度,證實超速是悲劇的肇因之一;(二)臺鐵對於該路段的限速略低於理論最大安全度,説明臺鐵有將構成影響的外在因素考量進去,確保行車安全。
不管該班普悠瑪列車在新馬站過彎的真實速度為何,列車出軌事故所造成的創傷都已經無法挽回。列車事故絕非單一的因素所造成,更加深入的機械工程原因是我們高中生無法探究的,還待專業的部門去解開謎團。作為高中生的我們,看到各種不同的説法與解讀,而感到困惑,也想要運用自己所學得出一個答案。經過查找相關必要的數據,計算出的結果可能與專業鑑定報告有所差距,但我們仍想讓學過的數學公式可以得到應用,為我們解答生活中遇到的問題,坐上「紙上談兵」的時光機,超越時空,陪伴他們「度」過回家的路。