現在,我們先問問自己:「你對數學有什麼感覺呢?」
最近為了準備線上課程,我和我的學生在舊金山街頭找了形形色色的路人進行訪談。我們訪問大約三十個人,有各種年齡、族裔、成就高低、社經背景。我們的訪談都用這句話當開場白:「能不能告訴我你對數學有什麼感覺?」
這透露了非常有趣的事,因為每個人會馬上告訴我們他們在學校時數學表現得如何。倘若我們問的是他們對藝術、科學或文學有什麼感覺,就不會發生這種情況。然而因為成長於看重表現的文化中,數學扮演了毫不留情的角色,被當成評判自身價值的衡量工具。
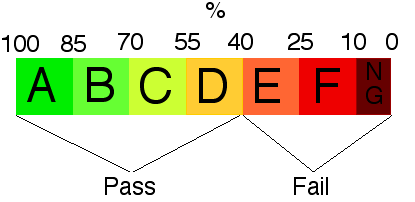
超前學習就是好嗎?學得快不如學得透徹
我經常遇到家長,對孩子在英語、科學等科目的學習泰然處之,但對於數學就緊張萬分。這樣的父母通常希望孩子能盡快學到進階數學,越早修進階數學課程越好,彷彿不這麼快學就會落後或是失去優勢。這很不幸,因為我們知道從小在數學上成績較好的學生,在他們學到低階數學時反而更傾向放掉數學。
比爾. 傑考(Bill Jacob)是加州大學的數學教授及加大學術委員會副主席,當學區和家長詢問他能不能讓學生提前修進階數學時,他建議不要,告知若急著學微積分,往往會造成準備不足,讓學生提早放棄,最後反而害了他們(Jacob, 2015)。
他還告知,微積分 BC 課程並不會讓學生的數學更上層樓,在低年級階段準備得更扎實,反而會讓學生有比較好的狀況。雖然大學很重視在高中階段修微積分的學生,但學生只需要在十二年級結束前修完微積分就行了,不必急著提早開始,只為了讓成績單更好看。此外,微積分也不是非修不可;我有幾個史丹佛的學生高中時就沒有修微積分,甚至還是理工科系的學生。

最近有個媽媽設法跑到我在史丹佛的辦公室來申訴,因為她的學區取消了進階班,結果變成所有的學生都能修進階數學。她一開口就極力指責我影響該學區的決策,但在我們的交談過程中,她經歷了各種情緒轉折,包括哭泣和如釋重負。她先是告訴我她女兒的前途已經毀了,因為她修不了進階數學課。
我於是向她解釋,學區替她女兒安排的學習軌跡仍然修得到微積分,她還是可以在自己的班級學到進階數學。我還建議,如果她的女兒需要接受更多挑戰,比較有效益的方式是把所學的觀念理解得很深入透徹,而不是快點學到進階的內容。交談過程中這位媽媽越來越平靜,離去時算是疑慮已消,只是依然打算要讓女兒「在家自學」──只有數學這一科。
只在意分數高低:贏在起跑點,卻輸在終點?
傳統的數學教學方式和已滲透進數學教學與學習的重表現文化,對高成就學生與低成就學生造成的傷害是一樣大的。研究結果顯示,有非常多的高成就學生放棄數學,而他們被推上進階數學課程與班級之後,概念理解力反而下降了(Paek & Foster, 2012)。
英國及國際數學奧林匹亞主席傑夫. 史密斯(Geoff Smith)最近公開談到讓學生倉促進階到更高的程度這件事。他表示,讓學生加速通過這個體系是「災難」也是「錯誤」,高成就的學生應該要深入探究數學,而不是匆促邁向更高的程度。不過,菁英主義的表現文化還會以另外一種方式傷害高成就學生,我們在為前途做出錯誤抉擇的學生人數上可看到這點。
你自以為擅長數學,對它又沒有愛,該如何堅持下去?
英國做過的一項研究顯示,不少大學生因為自己一向擅長數學而選擇數學當作大學科系,但當他們進了大學,卻發現身邊其他的同學跟他們一樣擅長數學(Solomon, 2007)。他們的自信心與自我認同在那一刻出現了危機(Wenger, 1998)。他們還沒有學會愛上數學或欣賞數學之美;相反地,他們是因為自己有能力做到,讓他們覺得自己特別好,才選擇了數學。
在顯然和他們一樣「特別好」的眾人環繞之下,他們失去了目標,領悟到自己從未對數學本身產生興趣,最後決定放棄(Solomon, 2007)。走上大學數學這條路卻發現自己並不是真正想讀數學的學生人數,與可能可以讀且喜歡讀數學、卻被學校賦予數學的錯誤形象打退的學生人數,兩者的比例大概是一比一百。

數學的三個層面:只懂程序但不懂意義是不夠的
Youcubed 平台的執行總監凱西. 威廉絲(Cathy Williams)在來到史丹佛之前,是學區數學科主任,她的工作是和前來理論的家長面對面接觸,這些家長多半是想爭取孩子修進階數學課的機會,因為他們的孩子程度很好又很聰明。
碰到這種情況,威廉絲都會提議和他們的孩子會面,然後為這些孩子做一次數學評鑑,好讓她了解他們的需求。結果威廉絲總是發現這些學生對於程序的反應很快,但沒辦法理解數學的意義,或是解釋不出觀念為什麼合理。舉例來說,這些學生算得出 1÷3/4 的答案是 1 又 1/3,可是他們無法解釋自己算出的答案為什麼是合理的。
威廉絲讓那些家長明白,數學是一門很寬廣的科目,不是只有計算與求快,而是牽涉到觀念的理解。她給他們看一張圖,上面畫出數學的三個層面。
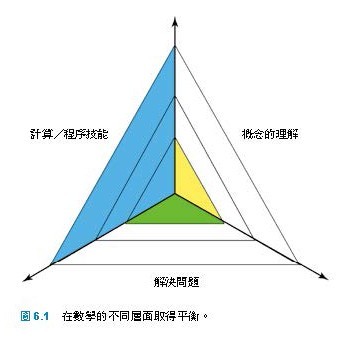
接著她向那些家長說明,他們的孩子只在其中一方面有很強的能力,而在另外兩個重要的數學面向才剛要開始累積實力;他們的孩子需要的不是更多的數學內容,而是需要多多理解他們已學過的數學,在反覆練習程序之餘,要能夠應用數學觀念。這些都是雇主最需要的數學思維。
菁英主義bye bye,人人都能欣賞數學之美
重表現的菁英主義文化充斥在數學中,並不是老師的錯,因為數學老師也受績效考核,就和他們的學生一樣。錯在我們的文化喜歡拿數學當作揀選機制和判定資優生的指標。
不管對高成就還是低成就學生來說,數學都亟需改變,要從被當作學生(和老師)排名分類依據、菁英主義且重表現的科目,變成開放、重視學習的科目,因為目前高成就學生棄數學而去的人數刷新紀錄,而低成就學生又被擋在門外,接觸不到他們完全有能力學習的觀念。
許多人同意,學生需要正面的思維信念,但假如我們真的希望給學生這些觀念,那就必須從根本改變美國社會中呈現及傳授數學的方式。我在給 Youcubed 每位訂閱者的電子郵件信末都會附一句話:「Viva la Revolution!」(革命萬歲!)我這麼做的原因是,我很清楚我們需要一場革命,要改造大家對數學、對這個科目、對學生潛能和思維模式的既有信念;要摒棄充斥在此科目中的菁英主義;要從表現轉向學習;要接受數學是多元的、美的、人人都能學習的科目。
本文摘自《幫孩子找到自信的成長型數學思維》,2018年12月,臉譜出版。




































