旅鴿:曾與智人一樣多的鳥類
住在北美洲的旅鴿(passenger pigeon,學名 Ectopistes migratorius)是種非常獨特的鳥,最特殊的是牠們的數量,毫無疑問排名美洲第一,或許也是世界冠軍——全盛時期估計有30到50億。然而,不久前仍如此龐大的族群,竟然已經步向滅亡的命運,1914年以後,世界上就再也沒有旅鴿了。

古代 DNA 近來成為研究滅絕生物的利器,而消失不久、目前仍有不少標本保存在博物館的旅鴿,它的基因組也在其滅絕的一百週年,也就是2014年時被定序發表。這項由台灣學者主導的研究,最驚人的發現是:旅鴿的遺傳多樣性與牠們龐大的鳥口數目,完全不相稱。[1]
通常我們會直覺地認為,某種生物的數目愈多,其遺傳多樣性應該也會愈大;旅鴿可能一度是世界上最多的鳥類,有如此多個體能累積遺傳差異,DNA 多樣性應該會大的嚇死人。可是由基因組看來,旅鴿的遺傳變異反而低的驚人,如果不考量旅鴿的個體數量、單純從他們的DNA序列來估計鳥口的話,估計值只有大約 33 萬左右……對,單位沒有寫錯,但旅鴿實際上至少有 30 億個體啊!

為什麼旅鴿的族群很大,遺傳多樣性卻很低?
為什麼旅鴿數量的理論估計與實際情況的落差會這麼巨大呢?影響遺傳多樣性的因素除了個體數目以外,還有何方神秘力量?在2017年發表的論文,提出相當具有啓發性的解釋,讓旅鴿無法累積 DNA 變異的主要因素是:天擇!?[2]
讓我們來從頭說起:新發表的論文獲得了更多旅鴿的 DNA 序列,包括 2 個新的基因組(加上之前發表的一共有 4 個),以及 41 個粒線體 DNA。除此之外,還定序了旅鴿的近親班尾鴿(band-tailed pigeon,學名 Patagioenas fasciata)的 2 個基因組,一同用於研究旅鴿的遺傳史。
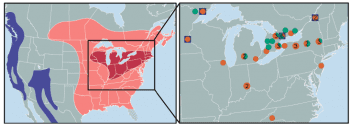
用 DNA 差異計算出的族群大小稱為「有效族群量(effective population size)」,採用粒線體 DNA 估計的結果是 1300 萬,比之前計算的 33 萬高出不少,不過仍遠遠低於實際上的 30 到 50 億。和班尾鴿比較,更能看出旅鴿反差的驚嚇程度,旅鴿的鳥口遠遠超過這種親戚,基因組的 DNA 多樣性卻只有班尾鴿 2 倍;假如以「有效族群量除以實際族群量」換算,也就是反差愈大、數值愈小,班尾鴿是 0.2,亦即實際鳥口是遺傳估計值的 5 倍,而旅鴿約為 0.0002,足足有 5000 倍之多!
與天擇利害糾葛,沒有中立空間
為何旅鴿的個體變多,卻無法累積相應的遺傳多樣性?我們常常聽到「多樣性大便是好的」,這背後的潛台詞是:多樣性小,代表個體數少,容易近親交配,導致不良後果。但是回頭思考,憑什麼族群個體變多,多樣性也要跟著變大?這是有前提的,那就是新的遺傳變異是中性的,亦即對個體沒有利、也沒有害;在沒有利害關係之下,新突變造成的 DNA 差異能保留在基因組中,因為每隻鳥的突變機率一樣,所以族群中有愈多個體、就會有愈多差異,使得族群整體的遺傳多樣性愈大。
可是實際上,個體間許多遺傳差異並非中性,而是會影響生存與繁殖。這又有兩個可能,一種是有利的,亦即有此變異與沒有此變異的個體相比,會比較有優勢;另一種是有害的,分配到這類變異的鳥比較倒霉,傳承後代的機率較低。以上是路邊過馬路的老爺爺老太太和扶他過馬路的我們都知道的天擇。
以 DNA 差異來看,牽涉利害關係的天擇多半會降低多樣性:舉例來說,如果單一品牌的市占率上升、或是一個牌子長保穩定優勢,會讓新品牌不易進入,「品牌多樣性」便會下降;相對的,如果大家都不挑品牌、買東西都碼是隨機選擇,那麼當有新品牌進入市場時,我們就多了一個牌子可以挑選、讓品牌多樣性變大,而之後影響其興衰的就只是機率而已了。
在演化上,隨機影響力的正式名詞叫作「遺傳漂變(genetic drift)」,它和非隨機的天擇都會影響 DNA。演化理論預測,比較大的族群中天擇的作用較強;比較小的族群遺傳漂變則較有影響力。旅鴿和班尾鴿相較,兩者多數特徵都差不多,旅鴿族群卻大了很多倍,應該會更強烈被天擇影響。那麼天擇的強大,與旅鴿遺傳多樣性不如預期之間,有關係嗎?
同一條染色體上不同區域,遺傳多樣性竟然不一樣?
分析基因組後觀察到的狀況非常奇妙,不過要解釋起來也很複雜,希望以下文字能正確傳達論文的概念。旅鴿染色體不同的位置,遺傳多樣性有明顯的差別。在同一條染色體的中間,遺傳多樣性普遍較低,而邊緣區域則顯著較高。相比之下,班尾鴿染色體不同區域間,遺傳多樣性的差異程度遠遠不如旅鴿劇烈。
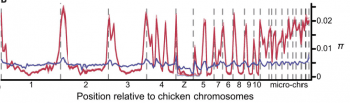
論文指出此一分佈模式,與染色體重組率(recombination rate)的高低一致,鳥類 DNA 重組率低的區域,也就是染色體中央的多樣性也低,重組率高的邊緣,多樣性也比較高 [3]。重組的影響是什麼?根據論文的說法,要與天擇的作用一起看。一個遺傳變異若是有利益糾葛,受到天擇作用時,影響的往往不是只有本身,還包括周圍的 DNA 序列,也就是遺傳學上說的「連鎖」。本身為中性的 DNA 片段,若是鄰居有利也會跟著受益,更容易傳遞下去,反之亦然。
天擇會消滅差異,除非被重組拯救
在強大天擇力量的影響下,由於遺傳連鎖之故,整段 DNA 都不容易累積差異;就像買 A 牌手機,連帶也會買整套 A 牌週邊配備,壓縮他牌的空間;假如重組率低,連鎖的範圍較大,天擇能影響的範圍也會跟著變大,正是旅鴿染色體中央的狀況。相對的,在基因組中重組率高的區域,比較不受天擇與連鎖的影響,中性變異的生還率高,也就能觀察到族群個體很多之下,遺傳多樣性應有的上升。

論文還做了一些細緻的分析,對相關議題有興趣的讀者請自行欣賞。跳到結論,不論是有害變異的清除(淨化選汰,purifying selection),或是有利變異的增加(正向選汰,positive selection),旅鴿整個基因組受天擇的影響都更勝班尾鴿。可見族群較大,的確也會有較強的天擇力量。
天擇兩個方向中,吻合淨化選汰特徵的 DNA 變異,比較旅鴿基因組中,重組率不同的區域,不管高低皆有明顯差異,意謂掃蕩有害變異的能力都比較強;但是重組率高的區域內,儘管序列乍看之下符合正向選汰的特徵,論文卻警告,這可能只是染色體重組時 DNA 突變的傾向所致(AT 突變為 GC 的機率更高,影響序列判斷),而非讓有利變異更容易留下的演化力量作用。總之,旅鴿基因組受天擇作用時,顯然也受到重組機率影響。
比較具體的基因方面,旅鴿有 32 個基因疑似受到正向選汰影響,有些基因與免疫、壓力、吃飯消化有關。想來十分合理,鳥口多,大家住在一起也容易得到傳染病,需要較強的免疫力;另外,有人會因為人多而壓力大、感到恐懼,鳥也一樣。
所以一度繁盛的旅鴿,為何會滅絕?

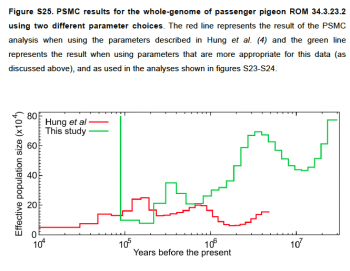
個人答案是:不知道,不過應該不單純。已經發表的 2 個論文,對這問題的見解不同。2014 年論文的論點是,旅鴿並非一直這麼多,牠們經歷過多次劇烈的鳥口波動,是導致其滅絕的重要因素。然而新的論文分析指出,過去幾萬年來旅鴿的族群量不斷增加,到 2 萬年前達到高峰,之後就一直保持穩定,直到滅絕,所以波動不像是主因。
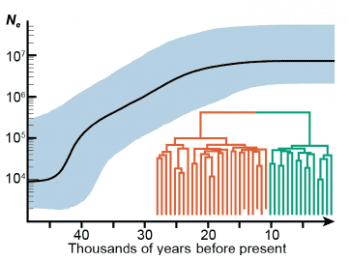
新論文的見解是,一度有利的天擇,讓旅鴿族群大增,卻也付出遺傳多樣性嚴重損失的代價,反倒使得環境轉變時,難以適應人類獵捕的壓力而短時間內徹底滅團。不過這個解釋……看起來也就只是另一個解釋,沒有進一步證據。
旅鴿的遺產
曾經能跟智人數目相提並論的旅鴿,消失一百多年。但是藉由研究牠們的 DNA 遺產,我們仍然能得到許多非常有價值的收獲。
一般認知中,族群大,遺傳多樣性也會跟著變高,然而旅鴿卻是極端的反例。對遺傳演化學家而言,即使都學過理論,知道大族群中天擇的作用力量也強,大概也難以想像現實世界中天擇的影響力,在極端龐大的鳥類族群中能如此驚人,強大到甚至會把正常累積的遺傳多樣性,大半排擠掉的境界。
重組率高低會導致基因組不同區域的 DNA 多樣性差異明顯,也告訴我們,探討抽象的演化力量作用時,不可忽略具體分子機制的影響。假如把旅鴿基因組視為一個整體,將無法釐清天擇的影響,而會把大部分區域錯誤地假設為中性演化,造成各種估計結果的偏差。
看完旅鴿的研究,雖然一些舊有認知受到挑戰,大家先別驚慌;也許旅鴿驚人的鳥口,讓牠們成為極端的特例,並非常態。可是回頭想想,遺傳學上大家研究最多,最在意的智人,不也是動物世界中,實際人口遠遠超過遺傳估計值的特例嗎?誰知道研究旅鴿獲得的知識,未來能有多少用於人類?
延伸閱讀:
參考文獻:
1. Hung, C. M., Shaner, P. J. L., Zink, R. M., Liu, W. C., Chu, T. C., Huang, W. S., & Li, S. H. (2014). Drastic population fluctuations explain the rapid extinction of the passenger pigeon. Proceedings of the National Academy of Sciences, 111(29), 10636-10641.
2. Murray, G. G., Soares, A. E., Novak, B. J., Schaefer, N. K., Cahill, J. A., Baker, A. J., … & Gilbert, M. T. P. (2017). Natural selection shaped the rise and fall of passenger pigeon genomic diversity. Science, 358(6365), 951-954.
3. Ellegren, H. (2010). Evolutionary stasis: the stable chromosomes of birds. Trends in ecology & evolution, 25(5), 283-291.
本文亦刊載於作者部落格《盲眼的尼安德塔石匠》暨其 facebook 同名專頁。