文/高崇文|中原大學物理系教授
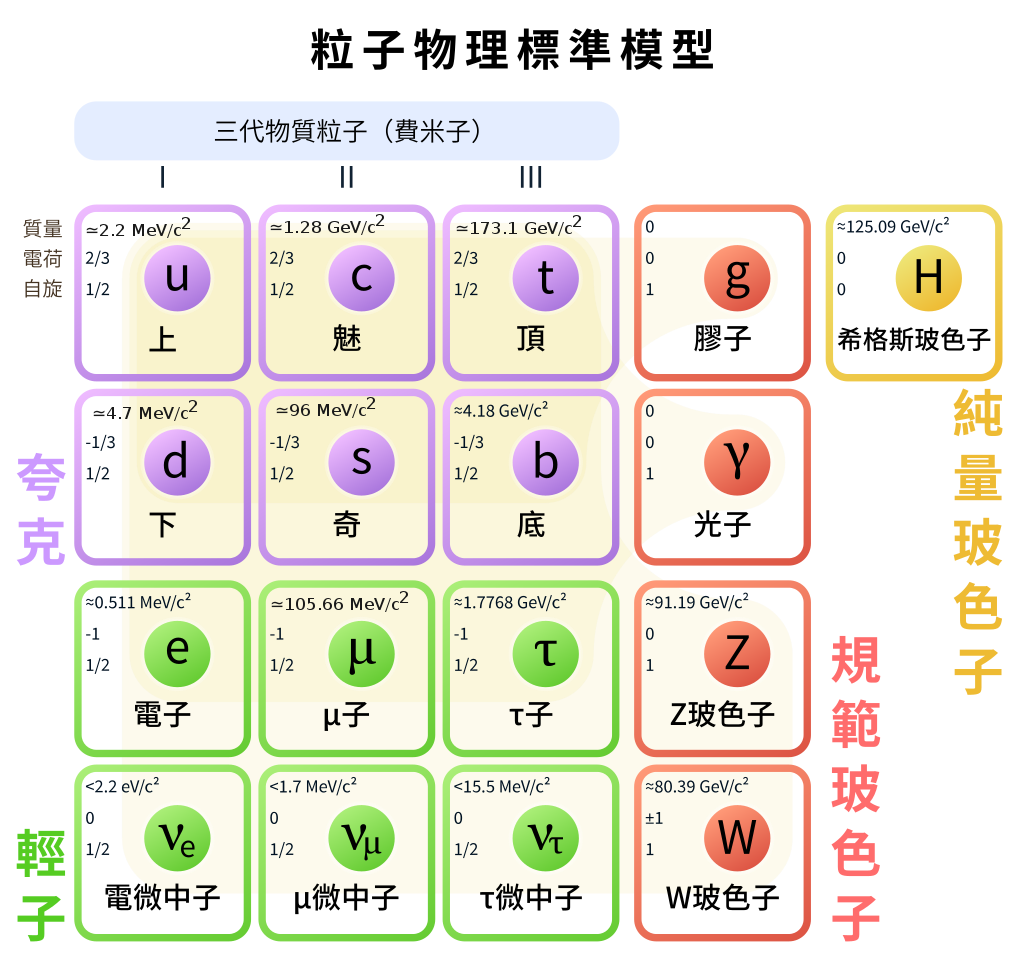
自從上世紀以來,我們一直以為物質世界是由一群自旋為 1/2 的費米子(Fermion)組成,而這些費米子藉著自旋為 1 的玻色子(Boson)交換動量與能量,其中電磁作用的媒介是沒有質量的光子,強作用透過沒有質量的膠子在夸克間來媒合形成強子,而弱作用則藉由相當重的 W 玻色子與 Z 玻色子來傳遞。這三個作用都可以用所謂的「規範場論」(gauge field theory)來描寫,而這些自旋為 1 的玻色子都是「規範玻色子」(Gauge boson)。
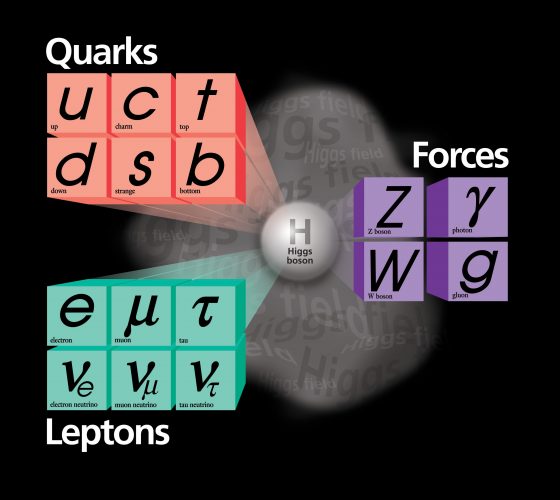
規範不變性(Gauge Invariance)保證了理論是可再重整化(Renormalizable)的「好理論」,可以系統性地處理掉量子場論中出現的發散問題,所以是不可或缺的。原本在規範不變性的要求下,這些玻色子都該是沒有質量的,而四年前發現的希格斯粒子則賦予原本該沒有質量的 W 與 Z 玻色子質量。希格斯粒子是目前唯一無自旋的基本粒子。
萬一我們又找到新的規範玻色子的話,那就表示新的作用力被發現了!
這可是非同小可,比起一般發現新粒子,發現全新的作用力是更加革命性的發現,這也是為什麼科學家不斷蓋能量愈來愈高的加速器,企圖尋找那些質量更高的未知粒子,特別是自旋為 1 的玻色子。
為什麼認定未知粒子的質量很高呢?那是因為質量不高的話,早就該出現在我們眾多實驗室的結果上了。然而,如果真的有前所未知的作用力存在於我們周遭,而它相應的玻色子(我們甚至不知是否有規範玻色子)與一般費米子的交互作用很微弱的話,那還是有可能會成了漏網之魚,逍遙於我們自認「無所不包」的粒子物理教科書之外。只有透過非常精密的實驗才能「補破網」,補捉到這些前所未知的新物理。
此外要測量質量非常低的粒子其實也是相當棘手的事情,這也是最近有人提倡的「第二個前沿」的原因。意即在追求更高能量的粒子物理實驗之外,也要努力提昇相對低能量的粒子碰撞實驗的精密度以及加強搜尋質量異常低的粒子。爾來最經典的例子就是對渺子-氫的蘭姆位移的精密測量,由它得到比通用值小 4% 的質子電荷分佈半徑。至今仍是一個待解的謎。
引發討論的「第五力」
編按:目前科學家知道物質間有四種基本交互作用力,分別為:重力交互作用(Gravitation)、電磁力交互作用(Electroweak interaction)、強交互作用(Strong interaction)和弱交互作用(Weak interaction)。
最近引發熱烈討論的所謂「第五力」其實也是這個方向的研究。乍看之下它只是個一般的核反應。匈牙利科學院 Attila Krasznahorkay 領導的研究團隊在 Debrecen 的核子物理實驗室花了過去三年的時間,研究一個特殊的核反應,他們將一顆質子打到鋰的同位素 Li7 形成鈹的同位素的激發態,然後處於激發態的原子核放出能量回到基態。
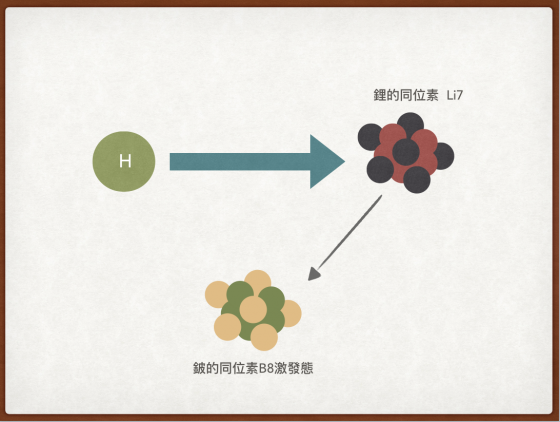
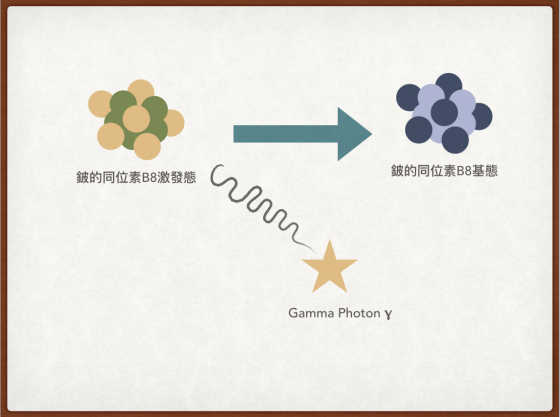
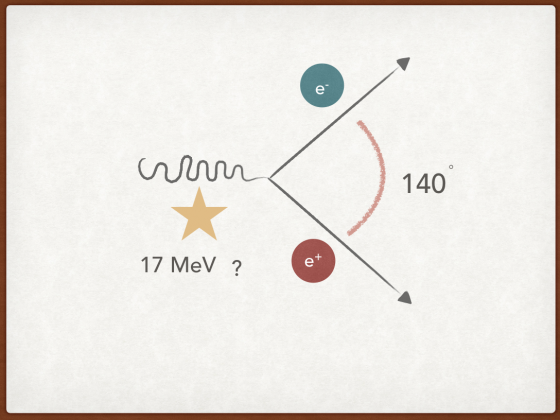
這些被放出的能量絕大部份會以光子型態釋放出來,但是有非常少的機會原子核會放出一個實光子一個虛光子,虛光子最後轉變成正負電子對。在標準模型中,這些能量一定是以光子的型態釋放出來,所以科學家們可以計算出正負電子對的四動量和的平方以及相應的正負電子的角度分佈。
令他們吃驚的是,實驗結果顯示觀察到的正負電子對似乎是由一個質量為 17 MeV 的中性玻色子所產生的!因為照計算正負電子對的數目應該單純地隨兩者之間的角度而減少,然而他們卻發現在角度在 140 度正負電子數目異常地多,這對應到的中間態其不變質量為 17 MeV。他們實驗做的非常精確,達到 6.8σ,這意味著這個「發現」只是統計產生的「雜訊」的機率只有 5.6×10–12!他們認為他們發現了一個自旋為 1、質量為 17 MeV 的新玻色子。這個結果登在今(2016)年一月的《物理評論快報》(Physical Review Letters)上。
有意思的是剛開始這篇論文並未引起太多討論。因為如果真有這麼一個新的玻色子存在的話,怎麼可能過去都沒發現呢?特別是它與電子跟核子(包含質子與中子)都必須有交互作用,而相關實驗數據早已汗牛充棟了。也許仔細分析之後這個「發現」就會如同其它類似的發現一般無疾而終吧!
但是在上個月在加州的加州大學爾灣分校的 Jonathan Feng 的研究群發表了他們的分析指出,如果這個 17 MeV 的中性玻色子與中子相互作用的程度遠高過與質子的交互作用的話,先前許多強作用實驗設定的限制都無法排除這個粒子存在的可能性。而它與電子的耦合強度約在 10–5 上下,現行的實驗只有給出上限約 10–3。所以到目前為止科學家們還無法找到與這個新玻色子存在相衝突的實驗證據。
此文一出,果然立刻引發熱烈的討論。當務之急,當然做更多的實驗。許多實驗室已經躍躍欲試了。其中最積極的莫過於位於維吉尼亞州的傑佛遜實驗室。傑佛遜實驗室原本為了尋找「暗光子」而設計了「暗光」(DarkLight)實驗,就是用一個電子轟擊一個質子來找尋末態會多出一個正負電子對的碰撞事件。原本正負電子對的能量是估計在 10 到 100 MeV 之間,現在他們將首先針對 17 MeV 附近做地毯式的搜索。
而兩個即將擁有正子束的實驗室:座落在羅馬近郊的 INFN Frascati National Laboratory 與座落在西伯利亞 Novosibirsk 的 Budker Institute of Nuclear Physics 也都將鎖定 17 MeV 來展開新一波的搜尋。它們將在明年啟動,屆時我們將會有更多的資訊,到時候到底匈牙利實驗室是否真的找到新的中性的 17 MeV 玻色子的謎底將會揭曉。
當然啦,也許會如同許多「著名」的實驗一樣只是空歡喜一場,但是萬一後續的實驗都證實了這個「厭質子」的新玻色子的存在,那麼新的粒子物理的嶄新一章可是將從一個匈牙利的核子物理實驗室中產生,那可真是叫人跌破眼鏡的。
身為強子理論物理學家的我,當然希望這個發現是新的突破,不過萬一這個新粒子被證實了,那麼還有許多迷團有待解決。它是基本粒子還是複合粒子?它是規範玻色子嗎?它對應的規範群是 U(1) 嗎?這些都是首先要回答的問題,再來還有如它與電子的交互作用為何比與夸克小兩個數量級?它與緲子有無交互作用?它是否可以解釋渺子的 g-2 的問題?它是否可以解釋「質子電荷半徑之謎」?這一些都還要等待下一波實驗才能逐漸闡明。
不過,我倒是覺得這是好機會來提醒莘莘學子,物理學之所以特別迷人,就是驚奇總是從你料想不到的地方出現,不要小看那些歷史悠久而又看起來平凡無奇的研究領域,說不一定哪天新一波的物理革命就從那裏開始呢!
參考資料:
- A. J. Krasznahorkay et al., Observation of Anomalous Internal Pair Creation in Be8: A Possible Indication of a Light, Neutral Boson, Phys. Rev. Lett. 116, 042501 – Published 26 January 2016
- Jonathan L. Feng et al., Protophobic Fifth Force Interpretation of the Observed Anomaly in 8Be Nuclear Transitions, Phys. Rev. Lett. 117, 071803 (2016) arXiv:1604.07411
本文轉載自《物理雙月刊》 38 期 8 月號,更多文章請見物理雙月刊網站。