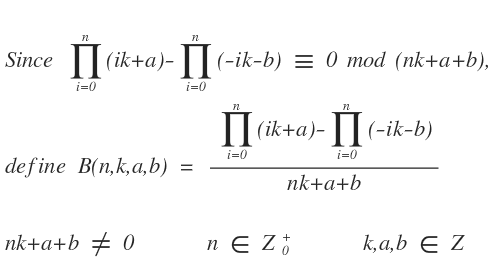2016 端午好運接「粽」而來,這段時間我與網友們聯合申請幾個數列成功,在此除了以較淺顯易懂的方式介紹 OEIS A274119 數列的故事,分享我們的喜樂之外,希望藉由這個故事,讓有志於數學研究的朋友參考,看能不能有更多有趣的數學新發現。
一切的故事從一題 2003 倍數開始,它是我小朋友學校所出的資優數學考題,題目是:
請問 (1 x 3 x 5 x ….. x 2001) + (2 x 4 x 6 x ….. x 2002) 是否為 2003 的倍數?
平時小朋友會分享學校有趣的題目,考驗看我會不會解,天啊,這題數目之大,一般計算機是算不出來的,還好我會用 Python 寫程式,可以驗算答案可以整除,但是個人並非數學系畢業,同時把這題目放在研發養成所部落格上看有沒有精簡有效解法。
那時沒有想到 modular arithmetic 可以輕易證明答案是整除的,這方法是網友 z423x5c6 所提供。
甚麼是 modular arithmetic?簡單說除法餘數可以加減乘除,看看幾個例子就懂,
5 / 11 = 0 … 5
2 / 11 = 0 … 2
(5 + 2) / 11 = 0 … 7
(5 x 2) / 11 = 0 … 10
(5 + 11) / 11 = 1 … 5
(5 – 11) / 11 = 0 … -6
A / B = C … D 在數學上除法餘數會用右式表示,A ≡ D mod B
只要證明(1 x 3 x 5 x ….. x 2001) + (2 x 4 x 6 x ….. x 2002) ≡ 0 mod 2003,就可解出來,
(1 x 3 x 5 x ….. x 2001) + (2 x 4 x 6 x ….. x 2002)
≡[1 x 3 x 5 x ….. x 2001 + (2-2003) x (4-2003) x (6-2003) x ….. x (2002-2003)] mod 2003
≡[1 x 3 x 5 x ….. x 2001 + (-2001) x (-1999) x (-1997) x ….. x (-1)] mod 2003
≡[1 x 3 x 5 x ….. x 2001 – 2001 x 1999 x 1997 x ….. x 1] mod 2003
≡ 0 mod 2003 整除
在求解題目時,與網友赤子西瓜同時發現如下規則,
(1 + 2) / 3 = 1
(1 x 3 x 5 + 2 x 4 x 6) / 7 = 9
(1 x 3 x 5 x 7 x 9 + 2 x 4 x 6 x 8 x 10) / 11 = 435
以及香港網友 flyingdusts 的提醒,1, 9, 435, … 在 OEIS 是一個全新數列,還沒人申請,因此大家聯名登記了這個數列 A273889。
我們四人都不是職業數學家,網友 flyingdusts 是香港一所小學的中文老師,沒錯就是中文老師不是數學老師,但對業餘數學非常熱愛;網友 z423x5c6 是一位維基百科的貢獻者,正準備就讀香港一所大學;網友赤子西瓜,雖然是一位國中一年級的學生,由於他的勤學,整體文化程度早已超過同齡的學子;而個人只是一位資深電子產品開發者,從我們的例子,可以了解數學的研究可以跨界合作,它也不是數學家專屬的工作,其實數學蠻貼近日常生活,只是大家沒特別留意而已。
OEIS (The On-Line Encyclopedia of Integer Sequences,整數數列線上大全)它是數學家尼爾·斯洛恩(Neil James Alexander Sloane)在 1960 年代中開始搜集整數數列,於 1996 年設置網站供大眾查閱,然後每年有上萬件各類研究者提供新數列登錄,從 A273889 就知道這是第 273889 號數列。
我們怎麼會知道這個全球性的數學資料庫?再把時間往前推移三年,在 2013 年暑假,我的小朋友當時考驗我一題總和 22,這題目的解法正是最近一部電影「天才無限家」主角拉馬努金所研究領域之一 ─ 整數分拆問題,為了求解它而開始研究 OEIS 數列。
計算數列的目的,個人原先以為只是為了科學研究,但研讀一些 OEIS 數列後,才發現有人用它記錄音樂旋律甚至數位圖檔!?其實 OEIS 資料庫登記的數列,以排列組合的數量佔最大宗,並且這個資料庫,現在約以每月上千筆資料的速度在增長。三年前查了一下,全台灣約十二人登記會員,有數條數列被核可,上千條資料補充,對數列有興趣的朋友可以加入研究行列,這甚至小學生都可以參加 (不過要會英文及寫程式),只要一張紙一枝筆以及一顆沉靜的心,應該可以尋找到自己的數列,就像天文學家在浩瀚的星空中尋找未名的星星一樣。
不過請注意,OEIS 是一個數列資料庫,許多科學論文與其連結,因此它要求刊登的內容必須正確無誤,並且具有實質意義的數列,而非硬湊出來的,除了內容說明以英文撰寫外,還須附上程式,如果知道公式也附上,建議數列項目 100 項以上,可以與他人聯名發表,並以真名發表,否則應該不會正式刊登。
在登錄 A273889 數列後,由於 z423x5c6 遲未申請 OEIS 帳號,無法將他同列數列作者群中,等他申請好了要加名,多數人持反對態度,並不認同他的數學證明貢獻就可以列名,因此鼓勵他另外申請一個他發現的三重階乘的 A274117 數列,
(1 x 4 x 7 + 2 x 5 x 8) / 9 = 12
(1 x 4 x 7 x 10 x 13 + 2 x 5 x 8 x 11 x 14) / 15 = 1064
同時,網友 z423x5c6 也發現 IBM 的研究員 Chai Wah Wu受到 A273889 證明的啟發又找出數列 A273983,表示這系列數列的新發現受到專家肯定,他發現的數列是,
(2 x 4 – 1 x 3) / 5 = 1
(2 x 4 x 6 x 8 – 1 x 3 x 5 x 7) / 9 = 31
(2 x 4 x 6 x 8 x 10 x 12 – 1 x 3 x 5 x 7 x 9 x 11) / 13 = 2745
受到這些數列研究的啟示,想找一個可以整合這些數列的公式,想出來之後,又再想有沒有通式可以整除,結果還真被我想到,
因此用它申請了 A274119,第一個以 Bridan formula B(n,k,a,b)公式申請的數列,
(2 x 2 x 2 x 2 x 2 + 1 x 1 x 1 x 1 x 1) / 3 = 11
(2 x 3 x 4 x 5 x 6 + 1 x 2 x 3 x 4 x 5) / 7 = 120
(2 x 4 x 6 x 8 x 10 + 1 x 3 x 5 x 7 x 9) / 11 = 435
以及第二個 B(2n+1,1,2,1) 數列 A274136,
(2 x 3 – 1 x 2) / 4 = 1
(2 x 3 x 4 x 5 – 1 x 2 x 3 x 4) / 6 = 16
(2 x 3 x 4 x 5 x 6 x 7 – 1 x 2 x 3 x 4 x 5 x 6) / 8 = 540
最後補充一些花絮,申請 A273889 數列時,網友 z423x5c6 未能列名,個人覺得非常遺憾,如果沒有他的幫助是不可能找到這麼多數列,因此在 OEIS 討論版以事實陳述並強烈推舉 z423x5c6 的貢獻,終於獲得 Sloane 首肯而名列作者群中,從這裡學到的經驗是正面的貢獻可以極力爭取應有的榮耀。還有申請數列時,了解台灣部落格文,美國竟然沒辦法直接閱讀,竟然要七十多歲的 Sloane 翻牆過來,光想像這畫面就又為這篇故事橫添一筆趣味!

目前找出這些數學式的感想為,以前大家都是在尋找一維的數列變化,但以後可能會出現很多這類二維數列(數列之間的關係),這算是這系列數列的創舉。
暑假將至,有興趣的朋友可以嘗試用 B(n,k,a,b) 尋找質數數列(2,3,5,7,11,13,…),到目前為止,還沒有人可以完整找到質數數列,如果你找得到,數學史絕對會記錄你的大名,因為目前是以數學質數保護密碼系統不易被破解,以前數學家採用多項式尋找,而現在多了一樣工具,或許可以挖到寶藏,從別人的研究再發現,科技的發展就是這樣慢慢進步的。