本文由民視《科學再發現》贊助,泛科學獨立製作
文 / Peter Chiang(中興大學物理系學生,大專足球運動員)
成功的香蕉球會完美地繞過防守的人牆,然後眼看就要飛到球門外時忽然一拐,直入球門!伴隨著裁判哨聲的,是守門員錯愕的表情及對手神秘的笑容。每次被對手以香蕉球進球,人牆中的我總會萬分懊惱,心裡又不屑地咕噥著:「你只是懂得利用流體力學而已!」
身為一個真實身分是足球員的物理系學生,當我想要踢出直直飛出去的球,我會讓腳著力於球面的中心(通常就簡稱球心);理論上,球將不會旋轉而直直朝著目標方向前進,並且會有最大的力道。當然,如果要使球飛高的話,可能需要朝著球心偏下一點點踢。而當我想要讓球路呈一完美弧線,我會偏左下或偏右下一點。

如果一個以左腳為慣用腳的球員(筆者慣用腳為左腳),選擇了綠色的點來做擊球點,球會朝著左前方的高空飛去。因為擊球點偏離了球心,於是會造成球的旋轉,你一定會認為球是朝著逆時針方向旋轉。然而,常看足球的人知道,足球員在踢自由球或角球時,都會稍微往側邊站一點。透過使腳踝呈L型、用腳內側摩擦球的邊緣,加強順時針旋轉的力道,使球路有漂亮的弧線產生。
日本山形大學的研究人員在 1998 年發表的論文中,利用 finite element analysis 來模擬足球員踢球的動作。研究確認了這個絕大多數足球員都知道的訊息-如果將踢球的點稍微偏離中心,並使腳和小腿呈 L 型,就能踢出香蕉球 [1]。下圖為山形大學團隊所模擬出的圖形。
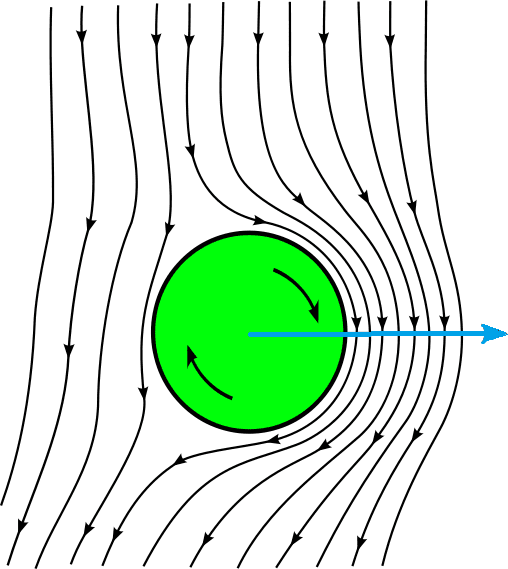
根據白努利定律,速度快的流體壓力會較小,反之則壓力大。因此可知,圖中的藍色箭頭指向球受力的方向。球路徑於是會成為一向右上運動的弧線。這就是著名馬格努斯效應(Magnus Effect)的應用。
這個道理同樣能夠運用在棒球、桌球及網球等 [2, 3]。當球員的腳離開球以後,因為速度相當快,球會先處在流體力學中所講的 turbulence regime,所受到的阻力相對較小。一旦球的速度降到某種程度,進入 laminar regime,球就受到阻力非常大的影響,而球的旋轉仍再作用。此時 Magnus Effect 的影響就變為明顯。這也是為何比賽常常會看到球直直朝觀眾席衝過去,在最後幾公尺忽然轉彎飛入球門的現象 [1]。
在某些特殊的狀況下,左腳的足球員會選擇用左腳的外側朝藍色的點踢過去,並摩擦帶動球以逆時針旋轉。這時候球就會朝著右前方飛出,繞過人牆,在飛向觀眾席的前一秒應聲 落入球門網中。這個高難度的動作需要足球員擁有強健的腳踝,有力的大小腿肌肉(使球能更快速地旋轉)及對身體的高度協調。知名的巴西球員 Roberto Carlos 就以這個技巧踢出了聞名世界的「The impossible goal」。
https://www.youtube.com/watch?v=8qH9ECcJ_DE
除了 Magnus Effect 之外,當然還有其他因素都還是有可能讓球的路徑跟預期的不同,如球表面的顆粒。2010 年南非世界盃所使用的球 Jabulani,就讓很多自由球高手表現失常。許多球員歸咎於球的重量,然而科學家發現其實球表面的光滑度不同反而是造成球路及速度和球員們以往經驗不符的主因 [4]。一個好的足球員,懂得利用不同的參數,為球隊創造出最佳的利益。
這幾年來我們的球隊被自由球殺的無地自容,但我永遠會記得大一那年,我們的俄國學長在中場以一球強而有力又刁鑽的香蕉球,帶我們進入了八強賽。我也永遠記得,那天我們順風。
參考資料
- The Physics of football. physicsworld [Jun 1, 1998]
- 馬格努斯效應。wikipedia
- What is the Magnus Force. YouTube
- Why the Adidas soccer ball, Jabulani, promises to confound goalies with its ‘otherworldly’ behavior. Design Engineering []
—————————–
更多內容也可以上科技大觀園搜尋「運動」,或每週六上午8點收看民視53台科學再發現。



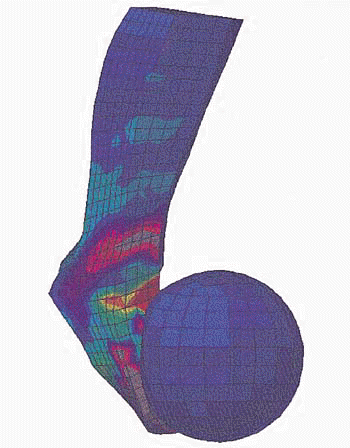






























-200x200.jpg)