簡瑋靚：別再說我們是用「擲筊」來播氣象了！

本文由 紐崔萊 委託，泛科學企劃執行。 

營養品的吸收率如何？

藥物和營養補充品，似乎每天都在我們的生活中扮演著越來越重要的角色。但你有沒有想過，這些關鍵分子，可能無法全部被人體吸收？那該怎麼辦呢？答案或許就在於吸收率！讓我們一起來揭開這個謎團吧！

當我們吞下一顆膠囊時，這個小小的丸子就開始了一場奇妙的旅程。從口進入消化道，與胃液混合，然後被推送到小腸，最後透過腸道被吸收進入血液。這個過程看似簡單，但其實充滿了挑戰。

首先，我們要面對的挑戰是藥物的溶解度。有些成分很難在水中溶解，這意味著它們在進入人體後可能無法被有效吸收。特別是對於脂溶性成分，它們需要透過油脂的介入才能被吸收，而這個過程相對複雜，吸收率也較低。

你有聽過「藥物遞送系統」嗎？

為了解決這個問題，科學家們開發了許多藥物遞送系統，其中最引人注目的就是自乳化藥物遞送系統（Self-Emulsifying Drug Delivery Systems，簡稱 SEDDS），也被稱作吸收提升科技。這項科技的核心概念是利用遞送系統中的油脂、界面活性劑和輔助界面活性劑，讓藥物與營養補充品一進到腸道，就形成微細的乳糜微粒，從而提高藥物的吸收率。

還有一點，這些經過 SEDDS 科技處理過的脂溶性藥物，在腸道中形成乳糜微粒之後，會經由腸道的淋巴系統吸收，因此可以繞過肝臟的首渡效應，減少損耗，同時保留了更多的藥物活性。這使得原本難以吸收的藥物，如用於愛滋病或新冠病毒療程的抗反轉錄病毒藥利托那韋（Ritonavir），以及緩解心絞痛的硝苯地平（Nifedipine），能夠更有效地發揮作用。

除了在藥物治療中的應用，SEDDS 科技還廣泛運用於營養補充品領域。許多脂溶性營養素，如維生素 A、D、E、K 和魚油中的 EPA、DHA，都可以通過 SEDDS 科技提高其吸收效率，從而更好地滿足人體的營養需求。

隨著科技的進步，藥品能打破過往的限制，發揮更大的療效，也就相當於有更高的 CP 值。SEDDS 科技的出現，便是增加藥物和營養補充品吸收率的解決方案之一。未來，隨著科學科技的不斷進步，相信會有更多藥物遞送系統 DDS（Drug Delivery System）問世，為人類健康帶來更多的好處。

小心啊，打雷囉，下雨收衣服啊！

氣象報告說好是晴天的，怎麼一踏出門就開始下雨了？

昨天都說要直撲的颱風，怎麼又彎出去了？

多麼希望天氣預報能做到百分之百正確，只要出門前問一下手機，就能確定今天是出大太陽還是午後雷陣雨，是幾點幾分在哪裡？又或是最重要的，颱風到底會不會來？

但你知道，現在的氣象預報，已經動用全球最強的超級電腦們了嗎？既然如此，我們現在的氣象預報能力到底有多準？我們什麼時候能徹底掌握這顆蔚藍星球上發生的所有天氣現象？

天氣預報有多困難？

雖然我們常常嫌說氣象預報不準、颱風路徑不準、預測失靈等等。但我們現在的實力如何呢？

目前美國國家海洋暨大氣總署的數據分析，對西太平洋颱風的 24 小時預測，誤差平均值約 50 英哩，也就是一天內的路徑誤差，大約是 80 公里。其他國家的氣象局，24 小時的誤差也約在 50 到 120 公里之間。台灣呢？根據中央氣象局到 2010 年的統計，誤差大約在 100 公里內。也就是臺灣對颱風的預測，沒有落後其他先進單位。

現在只要打開手機隨便開個 APP，就能問到今天的天氣概況，甚至是小區域或是短時間區間內的天氣預報。但在過去沒有電腦的時代，要預測天氣根本可以不可能（諸葛孔明：哪泥？）。

近代且稱得上科學的天氣預測可追溯回 1854 年，那個只能靠人工觀測的年代，英國氣象學家為了保護漁民出海的安危，利用電報傳遞來蒐集各地居民的觀察，並進行風暴預報。後來演變成天氣預報後，卻因為有時預報不準，預報員承受了輿論與國會批判的巨大壓力，最後甚至鬱鬱離世。

在電腦還在用打洞卡進行運算的年代，一台電腦比一個房間還大。氣象局要預測天氣，甚至判斷颱風動向，得要依賴專家對天氣系統、氣候型態的認知。因此在模擬預測非主流的年代，我們可以看到氣象局在進行預測時，會拿著一個圓盤，依據量測到的大氣壓力、風速等氣象值，進行專家分析。

當時全球的氣象系統，則是透過全球約一千個氣象站，共同在 UTC 時間（舊稱格林威治時間）的零零時施放高空探測氣球，透過聯合國的「World Weather Watch」計畫來共享天氣資料，用以分析。關於氣象氣球，我們之前也介紹過，歡迎看看這集喔。

也就是說，以前的颱風預測就是專家依靠自身的學理與經驗，來預測颱風的動向，但是，大氣系統極其複雜，先不說大氣系統受到擾動就會有所變化，行星風系、科氏力、地形、氣壓系統這些系統間互相影響，都會造成預測上的失準，更遑論模擬整個大氣系統需要的電腦資源，是非常巨大的。

那麼，有了現代電腦科技加持的我們，又距離全知還有多遠呢？是不是只要有夠強的超級電腦，我們就能無所不知呢？

有了電腦科技加持，我們的預報更準了嗎？

當然，有更強的電腦，我們就能算得更快。才不會出現花了三天計算，卻只能算出一個小時後天氣預報的窘況。但除了更強悍的超級電腦，也要更先進的預測模型與方法。現在的氣候氣象模擬，會先給一個初始值，像是溫度、壓力、初始風場等等，接著就讓這個數學模型開始跑。

接著我們會得到一個答案，這還不是我們真正要的解，而是一種逼近真實的解，我們還必須告訴模型，我容許的誤差值是多少。什麼意思呢？因為複雜模型算出來的數值不會是整數，而是拖著一堆小數點的複雜數字。我們則要選擇取用數值小數點後 8 位還是後 12 位等等，端看我們的電腦能處理到多少位，以及我們想算多快。時間久了，誤差的累積也越多，預測就有可能失準。沒錯，這就是著名的蝴蝶效應，美國數學暨氣象學家 Edward Norton Lorenz 過去的演講題目「蝴蝶在巴西揮動了翅膀，會不會在德州造成了龍捲風？」就是在講這件事。

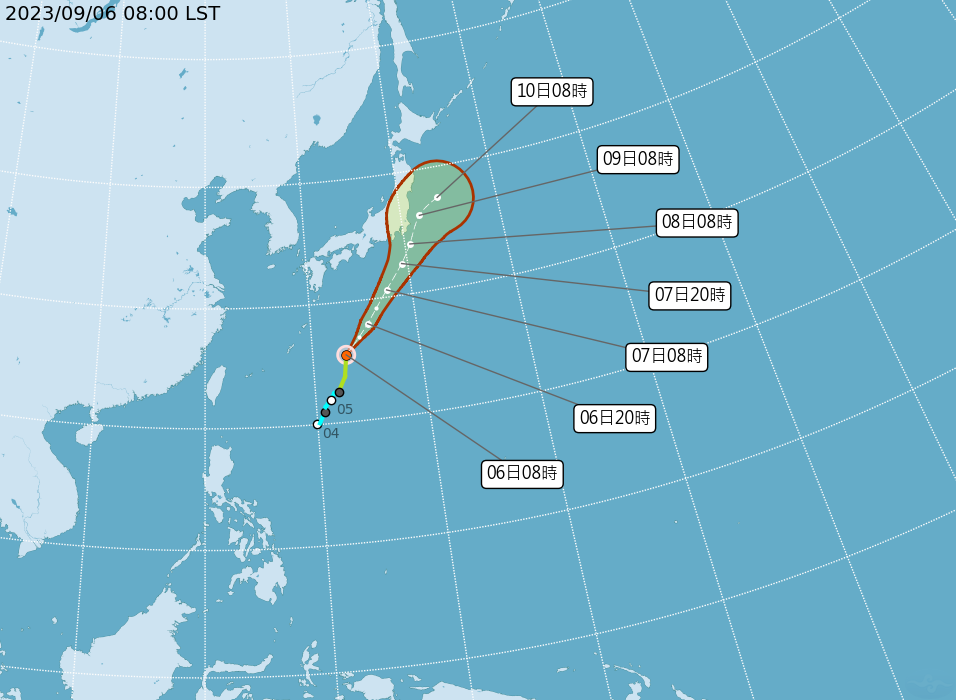
回到颱風預報，大家有沒有發現，我們看到的颱風路徑圖，颱風的圈怎麼一定會越變越大，難道颱風就像戶愚呂一樣會從 30% 變成 100% 力量狀態嗎？

其實那不是颱風的暴風圈大小，而是颱風的路徑預測範圍，也就是常聽到的颱風路徑潛勢圖，​是未來 1 至 3 天的颱風可能位置，颱風中心可能走的區域​顯示為潛勢圖中的紅圈，機率為 70%，所以圈圈越大，代表不確定性越大。​

1990 年後，中央氣象局開始使用高速電腦，並且使用美國國家大氣研究中心 (NCAR) 為首開發的 Weather Research and Forecasting 模型做數值運算，利用系集式方法，藉由不同的物理模式或參數改變，模擬出如同「蝴蝶效應」的結果，運算出多種颱風的可能行進路線。預測時間拉長後，誤差累積也更多，行進路徑的可能性當然也會越廣。

「真鍋模型」用物理建模模擬更真實的地球氣候！

大氣模擬不是只要有電腦就能做，其背後的物理複雜度，也是一大考驗。因此，發展與地球物理相關的研究變得非常重要。

2021 年的諾貝爾物理學獎，就是頒給發展氣候模型的真鍋淑郎。他所開發的地表模式，在這六十年間，從一個沒考慮地表植物的簡單模型，經各家發展，變成現在更為複雜、更為真實的模型。其中的參數涵蓋過去沒有的植物反應、地下水流動、氮碳化合反應等等，增強了氣候氣象模型的真實性。

當然，越複雜的模型、越短的時間區間、越高的空間精細度，需要更強大的超級電腦，還有更精準的觀測數據，才能預測接下來半日至五日的氣象情況。

世界上前百大的超級電腦，都已被用來做大氣科學模擬。各大氣象中心通常也配有自己的超級電腦，才能做出每日預測。那麼，除了等待更加強大的超級電腦問世，我們還有什麼辦法可以提升預報的準度呢？

天氣預報到底要怎樣才能做得準？

有了電腦，人類可以紀錄一切得到的數據；有了衛星，人類則可以觀察整個地球，對地球科學領域的人來說，可以拿這些現實資訊來校正模擬或預測時的誤差，利用數學方法將觀測到的單點資料，乃至衛星資料，融合至一整個數值模型之中，將各種資料加以比對，進一步提升精準度，這種方法叫做「資料同化 (Data Assimilation)」。例如日本曾使用當時日本最強的超級電腦「京」，做過空間解析度 100 公尺的水平距離「局部」超高解析氣象預測，除了用上最強的電腦，也利用了衛星資料做資料同化。除了日本以外，歐洲中程氣象預測中心 (ECMWF)，或是美國大氣暨海洋研究中心 (NOAA)，也都早在使用這些技術。

臺灣這幾年升空的福衛系列衛星，和將要升空的獵風者等氣象衛星，也將在未來幫助氣象學家取得更精準的資料，藉由「資料同化」來協助模擬，達到更精準的預測分析。

如果想要進一步提升預報準度呢？不用擔心，我們還有好幾個招式。

人海戰術！用更多的天氣模型來統計出機率的「概率性模擬」

首先，如果覺得一個模型不夠準，那就來 100 個吧！這是什麼意思？當我們只用一種物理模型來做預測時，我們總是會追求「準」，這種「準確」模型做的模擬預測，稱為「決定性模擬」，需要的是精確的參數、公式，與數值方法。就跟遇上完美的夢中情人共度完美的約會一樣，雖然值得追求，但你可能會先變成控制狂，而且失敗機率極高。

不如換個角度，改做「概率性模擬」，利用系集模擬，模擬出一大堆可能的交往對象，啊不對，是天氣模型，再根據一定數量的模擬結果，我們就可以統計出一個概率，來分析颱風路徑或是降雨機率，讓成功配對成功預測的機率更高。

製造一個虛擬地球模擬氣象？

再來，在物理層面上，目前各國正摩拳擦掌準備進行等同「數位攣生 (Digital Twin) 」的高階模擬，簡單來說，就是造出一個數位虛擬地球，來進行 1 公里水平長度網格的全球「超高」解析度模擬計算。等等，前面不是說日本可以算到 100 公尺的水平距離，為什麼 1 公里叫做超高解析度？

因為 500 公尺到 1 公里的網格大小也是地表模式的物理適用最小單位，在這樣的解析度下，科學家相信，可以減少數值模型中被簡化的地方，產生更真實的模擬結果。

電腦要怎麼負荷這麼大的計算量？交給電腦科學家！

當然，這樣的計算非常挑戰，除了需要大量的電腦資源，還需要有穩定的超級電腦，以及幾個 Petabyte，也就是 10 的 15 次方個位元組的儲存設備來存放產出的資料。

不用為了天氣捐贈你的 D 槽，就交給電腦科學家接棒上場吧。從 CPU、GPU 間的通訊、使用 GPU 來做計算加速或是作為主要運算元件、到改寫符合新架構的軟體程式、以及資料壓縮與讀寫 (I/O)。同時還要加上「資料同化」時所需的衛星或是全球量測資料。明明是做氣象預報，卻需要等同發展 AI 的電腦科技做輔助，任務十分龐大。對這部分有興趣的朋友可以參考我們之前的這一集喔！

結語

這一切的挑戰，是為了追求更精確的計算結果，也是為了推估大魔王：氣候變遷所造成的影響必須獲得的實力。想要計算幾年，甚至百年後的氣候狀態，氣象與氣候學家就非得克服上面所提到的問題才行。

一百年來，氣候氣象預測已從專家推估，變成了利用龐大電腦系統，耗費百萬瓦的能量來進行運算。所有更強大、更精準的氣象運算，都是為了減少人類的經濟與生命損失。

對於伴隨氣候變遷到來的極端天氣，人類對於這些變化的認知還是有所不足。2021 年的德國洪水，帶走了數十條人命，但是身為歐洲氣象中心的 ECMWF，當時也只能用叢集式系統算出 1% 的豪大雨概率，甚至這個模擬出的豪大雨也並沒有達到實際量測值。

我們期待我們對氣候了解和應對的速度，能追上氣候變遷的腳步，也由衷希望，有更多人才投入地球科學領域，幫助大家更了解我們所處的這顆藍色星球。

歡迎訂閱 Pansci Youtube 頻道 獲取更多深入淺出的科學知識！

• 作者／ 班‧歐林 (Ben Orlin)；譯者／王年愷

若說人類「不擅長」機率，太過簡化又太讓人難堪了。

機率是現代數學裡一門相當精妙的分支，當中處處有悖論陷阱。即使是基本的問題，也可能讓冷靜無情的專家暈頭轉向。嘲諷別人機率算錯，就像是在笑他們怎麼那麼不會飛，或是怎麼那麼不會喝下一整個海洋的水，或是怎麼那麼不防火。

如果真要說句公道話，應該說人類處理機率的能力實在爛透了。康納曼和特沃斯基在心理學研究中發現，人類對於不確定的事件有頑固的錯誤想法。他們會一而再、再而三地高估可能性微乎其微的事件，並低估幾乎鐵定會發生的事件。

這沒什麼大不了的，不是嗎？老實說，我們什麼時候看過機率在真實世界裡冒出頭來呢？又不是一輩子都在想辦法抓住知識性的工具，讓我們也許能在每一個清醒時刻的種種不確定性混沌中稍稍有些安穩⋯⋯

好吧，為了以防萬一——本章是一個操作指南，說明各種不同的人類怎麼去思考不確定性。這個東西就算再難，也不表示我們不能拿它來玩一玩。

如果你是政治記者

哈囉！你是一位政治記者。你會報導即將到來的選舉。你會報導失敗的選戰。在罕見的特別日子裡，你甚至還會報導像是「政策」和「治理」的事。

另外，稍微不可能的事情發生時，你好像會感到困惑。情況並非一直如此。在某個遙遠的過去，你會把選舉視為無限可能的神奇時刻。你輕描淡寫最可能發生的結果來增加刺激感，讓每一場選戰看起來都像是比賽結束鈴聲響起時從中場丟球正中籃框定勝負的。

2004 年美國總統大選當天晚上，小布希在俄亥俄州領先 100,000 票，未開出的選票不到 100,000 張時，你卻說俄亥俄州的選舉結果「太接近，無法確定」。到了 2012 年的總統大選，機率模型預測歐巴馬獲勝的可能性是 90%，你卻說選戰是「兩邊都有可能贏」。

然後，2016 年又把你的世界完全顛倒過來了。川普贏了希拉蕊．柯林頓。第二天醒來時，你覺得你經歷了一次量子奇異點，選舉結果就像是一隻突然憑空冒出來的兔子一樣完全無法預料。但對機率學家席佛（Nate Silver）及看法相近的人來說，這個結果只不過有一點意外而已，發生的機率為三分之一—就像丟骰子丟出 5 或 6 一樣。

如果你是氣象預報員

哈囉！你是一位氣象預報員，是電視上的雲層先知。你的一舉一動都自信滿滿，每一次交談的結尾都是「現在把現場交還棚內主播」。

另外，你會故意把機率說得模稜兩可，讓觀眾不會對你生氣。當然，你會盡可能誠實。如果你說明天的降雨機率是 80%，你所說的完全正確：在這樣的日子當中，降雨的日子總共有 80%。

但是，當降雨比較不可能發生時，你會誇大這些數據。你害怕有人把雨傘留在家裡，天空卻下起雨來，他們跑到網路上罵你。因此，當你說明天降雨機率是 20% 時，這種日子實際上只有 10% 會降雨。你會增加機率，來減少觀眾的咒罵。

假如觀眾更了解機率是什麼，也許你就能夠說出真話。當觀眾聽到「10%」的時候，好像會理解成「不會發生」。假如他們真的理解真正的意思（「每十次會發生一次」），你就能放鬆講出心裡真正想說的數據。在這一天到來以前，你仍然只能兜售半真半假的數據。

現在把現場交還棚內主播。

如果你是千年鷹號太空船船長

哈囉！你是「千年鷹號」（Millennium Falcon）¹ 太空船船長。你是一位星際暴徒、壞蛋，也是心腸寬大的俠盜。你一生的伙伴是一隻身上只穿一條子彈帶的 8 英尺長太空狗。

另外，你完完全全否認有「可能性」這件事。你不是一個會冷靜反思和考慮戰略的人。你會走私違禁品，也會顛覆整個帝國。你是快速拔槍殺人的冒險之士，只要稍有遲疑便會喪命，多猶豫幾下的話還會更慘。

在散兵坑裡沒有機率專家，而且你一生都躲在散兵坑裡。對你來說，繁複的機率算式只是累贅，和某個一直說「我的天啊」及「請容我建議」的神經質金色機器人一樣是拖油瓶。

我會覺得，我們每一個人的心裡都有一點你的特質。在需要冷靜、細心評估的時候，機率是相當有用的東西，但有時候我們需要一種自信，是頑強的量化數據給不了的。在需要直覺和行動的時刻，被機率拴住的人可能會畏縮，不敢跳出非跳不可的一大步。在這種時候，我們必須忘掉數據，儘管去飛。

註解：

1. 譯注：《星際大戰》中的宇宙飛船，用於走私業務，影史上最著名的太空船之一。

——本文摘自《塗鴉學數學：以三角形打造城市、用骰子來理解經濟危機、玩井字遊戲學策略思考，24堂建構邏輯思維、貫通幾何學、破解機率陷阱、弄懂統計奧妙的數學課》，2020 年 5 月，臉譜出版