台灣一年約有13萬對新婚夫婦。
但根據統計，民國九十九年，全台有高達58,037對夫妻離婚，平均下來一天有159對夫妻簽下離婚協議書，一小時6.6對，十分鐘1.1對。這是一組相當不浪漫的數字，對月下老人來說，綁了又解，解了又綁的，更造成嚴重的超時加班，導致迄今依然沒輪到我。有關單位必須正視這個問題，我建議將離婚定為法定傳染病，宣布台灣為疫區。不過這得挺住婚宴飯店還有婚禮相關產業的抗議，畢竟他們是離了又結的唯一受益者。
每一對夫妻，都想尋找一組能分析婚姻的方程式。知名心理學家提出一道只有減法的解答：
The frequency of love-making minus the frequency of quarrels.
－Robyn Dawes
好像怪怪的。這種事情，還是請數學家來解釋比較可靠。
※
牛津大學數學教授James Murray花了好幾年，邀請數百對夫妻到研究室，針對生活中特定主題對談，例如金錢、政治、兩性。他在一旁記錄聊天過程，分析夫妻對話互動：是笑到掉眼淚、還是講沒兩下就在比賽誰的眼白比較多，翻到抽筋也在所不惜。
利用互動中透露的細節，James Murray量化出夫妻情感。
以下是各種反應的量化分數。加四分最佳反應有：愛意、幽默、認同、喜悅；表現出「有興趣」，加兩分；沒有零分的反應；扣一分的負面反應：生氣、不講理、哀傷、發牢騷；扣兩分：挑釁、防禦、拒絕聆聽；臉歪一邊表露出「令人作嘔」扣三分；最嚴重的是「鄙視」，扣四分。
從這樣的量化結果可以得到一個結論，許多人常說另一半幽默很重要，反映在量化上也的確如此。此外，你可以氣一個人、討厭一個人，但你還是有可能愛他。唯有鄙視一個人是最糟糕的，畢竟，你不大可能愛上一個你瞧不起的人。
利用量化結果，去分析夫妻對話時的分數變化，以對話時間為x軸，可以得到下面的圖
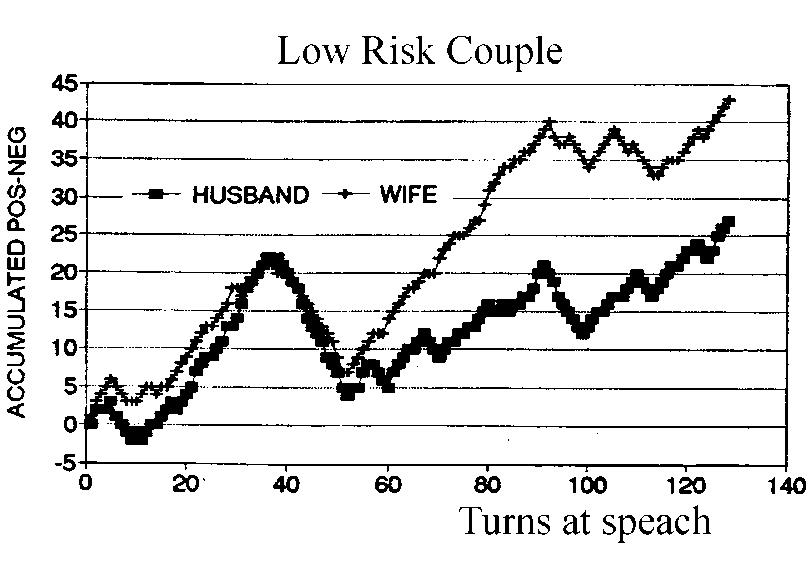
這是一對有著穩定婚姻的夫妻，好比布萊德彼特(Brad Pitt)與安潔莉娜裘莉(Angelina Jolie)，雙方互動有如剛發布iphone的Apple股票指數節節上升感情。若夫妻關係很差，分數將隨著時間不斷下跌。可以預見，最終將走上布萊德彼特與珍妮佛安妮斯頓(Jennifer Aniston)的離婚結局。
※
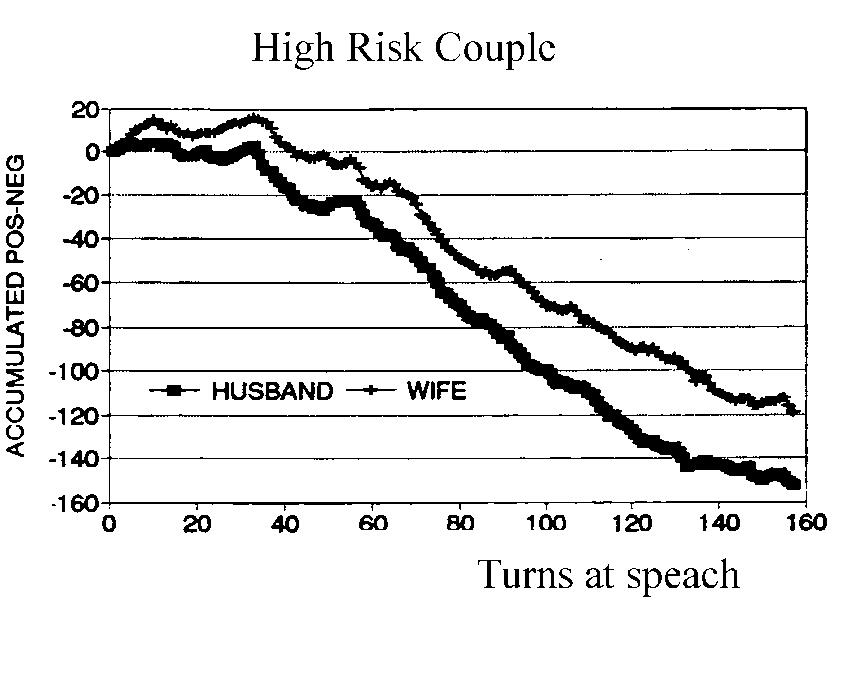
同樣一筆資料，要是將丈夫與妻子的分數分別當成x軸與y軸，可以得到下面的結果
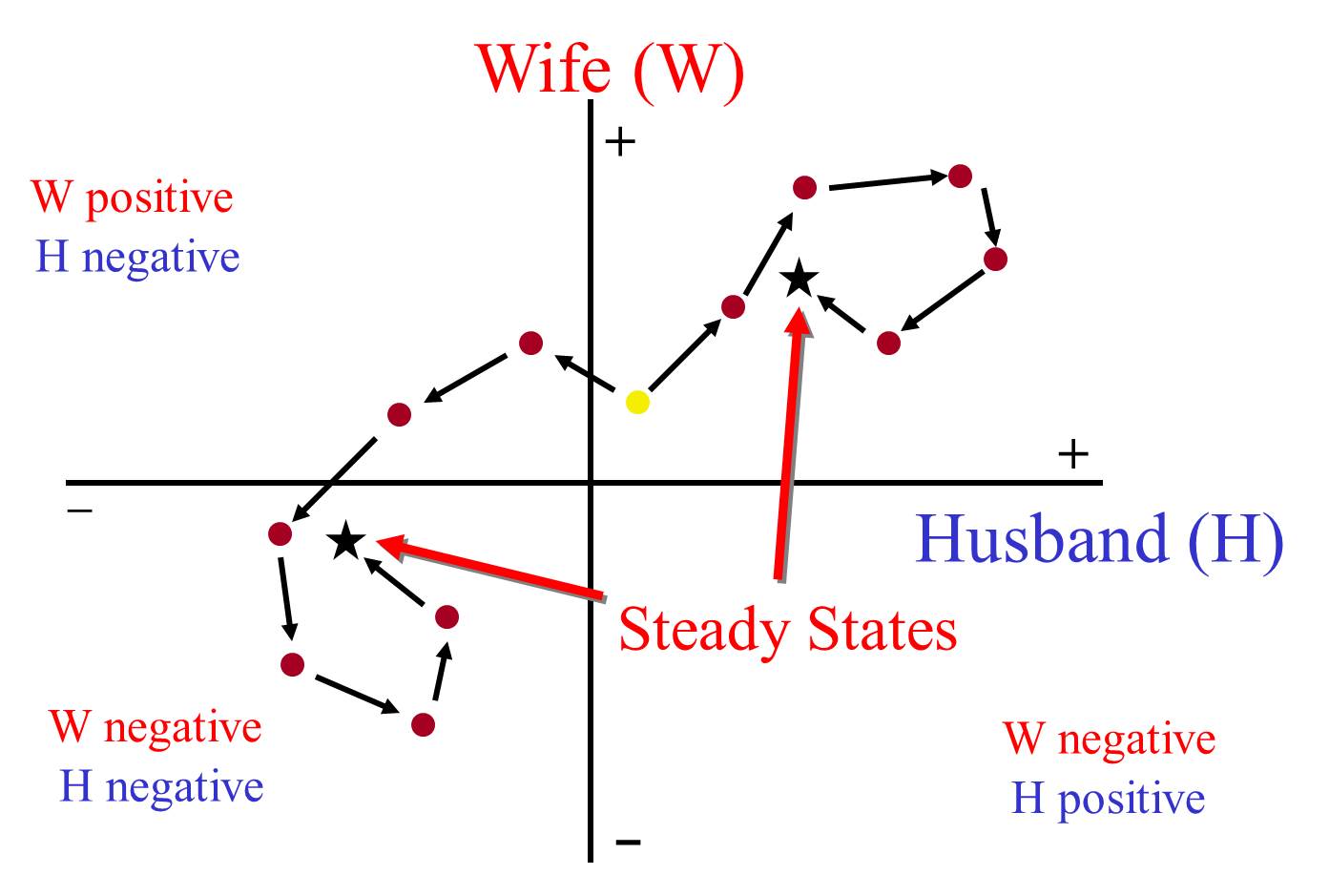
第一象限表示雙方都有好心情，第三象限是雙方都不開心，第二與第四象限則是各有一方開心，一方不悅。在這個例子裡，起始的黃點在第一象限，約莫是出門撿到十元的小確幸程度。接著依據向左走、向右走會出現兩種收斂狀況：往右，互動越來越好，開心過了頭，最後收斂回起始點右上方的星號，表示經過這次對話，雙方都更開心了。但也可能往左，丈夫先不開心，妻子看到丈夫「結屎臉」，好心情受到影響，也皺起眉頭，之後兩人大吵，把該摔的東西摔一摔，稍微冷靜後，收斂在左下角的星號，落在雙方都心情不好的第三象限。
※
James Murray進一步用遞迴數列模擬情感變化：
Wt+1=a +r1Wt+IHW(Ht)
Ht+1=b +r2Ht+IWH(Wt)
t是時間。Ht和Wt是丈夫和妻子在時間t的情感數值。(a,b)是妻子與丈夫的情緒起始值。(r1,r2)是前一刻情緒累積到這一刻的係數，越高表示越容易記得另一半對他的好，也越容易記得以前的不好。儘管，根據經驗，我認為念舊跟翻舊帳的係數應該有所不同。IHW(Ht)是方程式，表示此刻妻子受到丈夫前一刻反應影響的「影響方程式」。IWH(Wt)則是反過來妻子前一刻的反應，對此刻丈夫的影響。舉某位妻子的影響方程式為例，x軸是丈夫的情緒變化，y軸是妻子因此受到的情緒影響。
從這圖中，我們可以看見這位妻子的反應是：在一定範圍內，她的情緒隨著先生成正比。但超過一個範圍時，就會開始和先生唱反調。
相當符合經驗法則。
James Murray進一步將影響函式以二段式的線性逼近(piecewise linear)。繼續以上圖為例，當丈夫生氣時，線性逼近的線段斜率大於1，表示妻子會更激動，比丈夫更生氣；當丈夫開心時，線性逼近的線段斜率小於1，妻子比較沒那麼開心。
※
每一對夫妻，都有自己獨特的影響方程式。
有些夫妻在對方不爽時，會一點反應都沒有，有些則會放大對方的情緒。根據不同的影響方程式，James Murray將婚姻分成五種類型：
不穩定型(volatile)：浪漫、熱情，戲劇化。上一秒在客廳上演無差別格鬥，下一秒又在廚房激動地擁抱在一起。代表人物同樣請參考布萊德彼特與安潔莉娜裘莉合演的「史密斯夫婦(Mr. & Mrs. Smith)」。
理智型(validating)：冷靜、價值觀相當，細水長流。代表人物是經典大茂黑瓜廣告裡「老伴，明天吃素啊」的老夫老妻檔。
逃避型(avoiders)：感情好時什麼都願意分享，樂於表達自己的情緒。意見不合時盡量避免爭執，寧願躲到山上去找個樹洞大吼
「我老公是混蛋！！」
就算大吼時撞見另一半蹲在另一顆樹前，兩人也只會尷尬笑一笑說
「噢，你知道，我有個同事綽號叫老公…」
代表人物是瓊瑤小說裡的小媳婦。
這幾種類型的夫妻，儘管相處模式不同，但都有穩定的婚姻。
不穩定婚姻最主要的起因是夫妻個性不同。
敵意型(hostile)：妻子是不喜歡爭執的逃避型，但丈夫卻是理智型。每次都推推眼鏡，很理性地將妻子逼到牆角說
「妳如果有不滿，可以說出來，我們討論討論？」
「遇到問題不要逃避，逃避不能解決問題的。」
「我看得出來妳在不開心…」
明明是好心想溝通，但看在習慣逃避的妻子心裡卻滿不是滋味
肚子痛又不是放個屁就不痛了，好心忍著不放，有人卻不信邪，非得逼人放屁才甘願。
就算心裡這麼想，妻子還是說不出口。
分裂型(hostile detached)：妻子是熱情奔放的不穩定型，但丈夫是理智型。一直沒機會被推到牆上或餐桌，妻子覺得買那麼多塑膠碗盤真虧。好不容易灌醉丈夫，說服好他了，他卻先捲起袖子，收好餐桌上的碗盤，洗碗，烘碗，擦乾淨餐桌，最後遲疑了半秒說
「你確定餐桌不會垮嗎？」
可以確定的是妻子的臉一定垮了。
以上這些，是James Murray教授的婚姻方程式簡介。有興趣的話，不妨算算看你和另一半的影響方程式吧。
參考文獻
The Mathematics of Marriage: Dynamic Nonlinear Models(J. M. Gottman, J.D. Murray, Catherine C. Swanson, Rebecca Tyson, Kristin R. Swanson). MIT Press, Cambridge, MA, 2002.
註：更多賴以威的數學故事，請參考《超展開數學教室》。
- 愛因斯坦曾說，如果達文西留下的大批手稿能在當時發表，人類的科技發展，能提前半個世紀！
- 到泛科市集結帳輸入 panscihere 優惠碼，立即省 60 元
- 聲音的魔法！說話聲音可以提升別人對你的好感度？
- 雜物OUT！斷捨離的同時，也能整理思緒帶來好心情？
