 ▲我們的公投法的 「通過門檻函數」 不是一個單調遞增函數, 所以所有的公投拉票與辯論活動註定經常會離題失焦
▲我們的公投法的 「通過門檻函數」 不是一個單調遞增函數, 所以所有的公投拉票與辯論活動註定經常會離題失焦
五年前我寫過一篇 『都是 「非單調遞增函數」 惹的禍 (數學不及格的公投法)』, 以為這個簡單的數學觀察只需要稍微提醒, 數學程度普遍不錯的國人就會恍然大悟, 用輿論促成修法; 沒想到時至今日面對核四公投, 依舊是… 總統唸法律、 行政院長拼經濟, 數學程度不好都可以諒解 (抖); 但就連師大數學系畢業的立法院長也沒注意到這個問題… 只好細細重寫該文, 並且誠懇地拜託今天的高中數學老師把單調函數單元教好, 寄望至少等到下一代執政、 掌權的時候, 我們終於可有一部數學及格的公投法。 然後, 小格及泛科學的讀者, 也許就可以因此而原諒我竟然花這麼大的篇幅來談一個高一數學程度的問題。
一、 單調函數
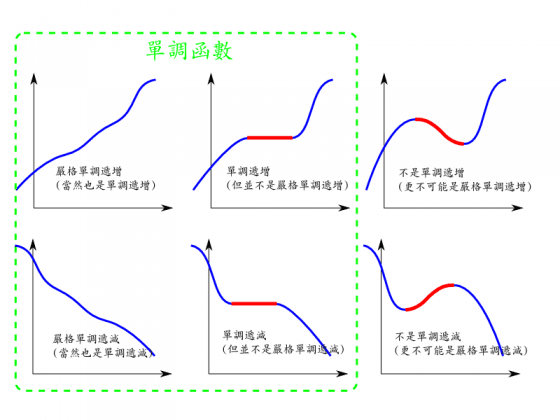
嚴格單調遞增函數 (或稱 絕對單調遞增函數) 用白話文講, 就是一路往上爬的函數。 換個方式說, 自變量 x 越大, 函數值 f(x) 就越大。 再換個方式說, 越往右邊走, 函數爬越高。 用嚴謹的數學定義來寫, f(x) 成為嚴格單調遞增函數的條件是: 每當 x1 < x2, 必然有 f(x1) < f(x2)。
單調遞增函數 用白話文講, 就是一路都至少不會往下掉的函數。 換個方式說, 自變量 x 越大, 函數值 f(x) 不是變大至少也保持水平。 再換個方式說, 越往右邊走, 函數爬越高, 或至少保持水平。 用嚴謹的數學定義來寫, f(x) 成為嚴格單調遞增函數的條件是: 每當 x1 < x2, 必然有 f(x1) <= f(x2)。
習題:
- 請模仿前兩段, 定義何謂嚴格單調遞增函數、 何謂單調遞減函數。 (提示: 先用白話文思考)
- 單調遞增函數跟嚴格單調遞增函數之間有什麼關係? (提示: 先用白話文思考)
- 請舉一個例子, 說明一個函數可能既不是單調遞增函數, 也不是單調遞減函數。 (提示: 先用白話文思考)
- 請舉一個例子, 說明一個函數可能既是單調遞增函數, 又是單調遞減函數。 (提示: 先用白話文思考)
- 加分題: 請用 Venn Diagram (文氏圖、 維恩圖) 圖示以上四類函數之間的關係。
嗯, 本文不附習題解答是故意的。 拜託讀者留言時不要洩露解答 — 就是要請沒把握的讀者拿本文去請教數學老師。
二、 投票通過門檻函數
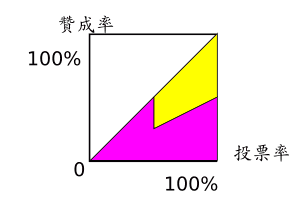
考慮一個投票的場合。 如果拿 「出席人數除以具投票權總人數」 當橫軸, 又拿 「贊成人數除以具投票權總人數」 當縱軸, 那麼每個投票結果可以用 單位正方形 上面或內部的一個點來表示。 例如假設全班 50 人, 某次投票有 32 人出席, 有 21 人投贊成票, 那麼這次的投票結果就可以用 (0.64, 0.42) 這個點在這張圖上標示。 顯然, 所有的點都必然落在單位正方形的右下半這個等腰直角三角形內。 (因為贊成人數必然小於或等於出席人數。) 對了, 以某次真實發生的投票的所有可能結果來說, 「具投票權總人數」 是一個常數, 所以以下在比較相對大小時, 有時就直接用 「贊成人數」 取代 「x 座標」, 用 「出席人數」 取代 「y 座標」。
本文只討論簡單的投票情境: 依據投票規則可以用這張圖上的一條固定的線區隔為 「通過」 與 「不通過」 兩區塊 (而不需要加入其他變數) 的狀況。 區隔這兩塊區域的這條線, 姑且稱之為 投票通過門檻函數, 以下簡稱為門檻函數。 從數學的角度來看, 一個合乎情理的投票規則, 它的門檻函數圖形必須具有下列特性:
- 等腰直角三角形的右上角那個點 (代表 「全數贊成」) 應該落在 「通過」 區。
- 等腰直角三角形的下緣這條線 (代表 「零人贊成」) 應該落在 「不通過」 區。
- 門檻函數, 應該是一個單調遞增函數。 意思是: 越多人出席, 通過門檻的人數就應該越高, 或至少相同。 如果違反這條, 會造成 「多一個人來投反對票, 反而讓原本的不通過翻盤成通過」 的荒謬現象。
- 門檻函數, 最好近似一個連續函數。 意思是: 不要因為出席人數差一人, 投票通過門檻的人數就突然大幅上下跳動。 門檻函數如果違反這條特性, 那麼當 「具投票權總人數」 越大時, 「少數人出席與否 (跟他們投什麼票無關) 將決定投票結果」 的荒謬現象會越明顯。 (這一點, 雖然用微積分的術語會比較容易談, 但其實就算不懂微積分還是可以用常識理解。)
這條函數越高, 意謂著通過門檻越高; 這條函數越低, 意謂著通過門檻越低。 到底門檻多高或多低才合理, 那並不能只靠數學分析來回答, 所以那並不是本文討論的重點。 但不論門檻高低, 如果一條函數不能滿足上述四點, 它顯然就是一個數學不及格的門檻函數。
三、 一些例子
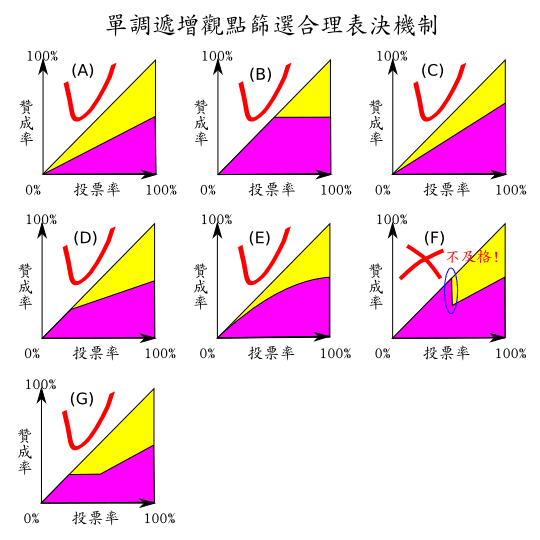
上圖是門檻函數的一些例子。
- (A) 是一個最簡單的門檻函數: 不管多少人出席, 總之出席人數當中, 過半贊成就通過。 但有人會擔心它的門檻過低。
- (B) 是一個很嚴格的門檻函數: 不管多少人出席, 總之具投票權總人數當中, 過半贊成才通過。 但這意味著: 不關心投票議題或因為其他原因而不出席的人通通被算成反對。 也就是說, 投票結果永遠傾向 「不通過」; 正面或反面設定議題, 將改變雙方優劣勢。
- (C) 是也是一個很嚴格的門檻函數: 不管多少人出席, 總之出席人數當中, 超過 2/3 贊成才通過。 但這有可能造成 minoritarianism(少數專斷) — 少數的反對可以否決多數支持者的意見, 因而正反面設定義題也會造成雙方有優劣勢之別。
- (D) 超過一定比例 q (例如 1/4) 出席, 而且出席人數當中超過一個浮動比例贊成, 才通過。 這個浮動比例從 x=q 時的 100% 逐漸降到 x=1.00 時的 50%。
- (E) 效果類似 (D), 但用一條圓滑曲線取代兩段直線, 例如 y=-0.5x^2+x。 這個函數具有以下特性: 當 x=0 時, y=0; 當x=1 時, y=0.5; 它在這個範圍內嚴格單調遞增; 它在 (0,0) 的切線正好是 y=x。
- (F) 我們的公投法。 它違反第二節所講的門檻函數第三、 第四兩個特性, 所以同時具有上述兩大荒謬現象; 而所有的公投拉票與辯論活動也將註定經常會離題失焦。 它很容易被政客扭曲操作, 讓大眾忘記原始議題。 最後, 當投票率低於 50% 時, 它跟 (B) 一樣, 門檻高到毫無道理; 當投票率超過 50% 時, 它卻又跟 (A) 一樣, 毫無額外門檻效果可言。
看完這篇之後, 還能開口支持 (F) 的人, 不是自己高中數學不及格就是別有居心, 鄙視並且蓄意欺騙他的聽眾。[抱歉, 先前態度不好又沒禮貌, 我收回這句話。 後來很訝異地被說服: 一個人其實並沒有惡意, 但只是因為成見和過度的自信讓他無法接受簡單的事實, 這樣的事是有可能發生的。] - [3/9 更新] (G) 感謝 explorer 3月4日上午9:22系列留言提供 另一個方案 的討論連結及自製圖示。 贊成人數超過反對人數, 而且具投票權者超過一定比例 (例如 25%) 投贊成票才通過。 這個單調遞增函數跟 (D)、 (E) 一樣具有額外保險門檻效果, 而且法律文字很好寫。
四、 結語
從數學的角度來看, (A) 其實是比較對稱的 — 不會有 「議題正反面設定」 的爭議, 也比較符合 奧卡姆剃刀原則 Occam’s razor。 但如果害怕低投票率時門檻過低, 又不希望高投票率時讓少數人有專斷的機會, 而且也不太介意 「議題正反面設定」 有一點差別 (以致允許政客有一些操弄的空間) 那麼 (D) 或 (E) 之類的函數可能是比較理想的門檻函數。
改採 (D) 或 (E) 類型的門檻函數, 比較大的現實挑戰是: 那些沒有達到高一數學程度的公民, 恐怕很難理解。 話說回來, 經過這篇文章提醒之後, 那些數學程度超過高中的公民, 恐怕更難接受現在這個明顯數學不及格的公投法 (F)。 最終, 我們會不會改成 (D) 或 (E) 或其他至少符合三、 四特性的門檻函數? 或是我們會維持 (F), 讓其他國家及後世嘲笑臺灣人數學教育的失敗? 這個問題的答案, 也將透露我們的政府/民意代表/媒體/老師到底是致力於培力 (empower) 公民, 或是致力於愚民。 [3/9 更新: 請見 (G), 既有 (D) 與 (E) 的優點, 又很容易寫成法律條文。]
[※ 3/6 回應]
以下回應對本文的挑戰及觀察。
有一類的挑戰, 主要圍繞著 「統計學」 這三個字。 我用 i.i.d 三個字母回應 — 。 在這裡想要套用統計學, 就先得用 「隨機選取若干 “彼此獨立的固定機率伯努利分布”」 來描述有來投票的人。 但這個假設不只是太強, 恐怕跟事實完全不符。 還有這篇 「從公投投票率問題淺談二項分布與初等估計」 也犯了相同的錯誤。 還記得民進黨堅持公投綁大選, 國民黨卻叫大家拒領公投票嗎? 請別告訴我你真的相信 「有去投票的那群人」 跟「沒去投票的那群人」 他們投贊成的機率, 有相同的期望值。 很多人 (包含我) 認為許多 (但非全部) 統計論述是超級大謊言 ( Lies, damned lies, and statistics) 就是因為經常看到這類與事實不符的底層假設被聽者甚至講者自己忽略忘記。
有一類的挑戰, 認為本文的二分法不完整, 其實應有三種狀況 (「支持、 反對、 不在乎」 或是 「通過、 不通過、 交由政府決定」 等等)。 我的回應是: 請見 公投法 第四章第30條。 一個公投只有「通過」與「否決」兩種結果, 所以一個門檻函數確實就真的只把等腰直角三角形 (所有的可能性) 切成兩塊。 當一個具體的投票結果出現之後 (例如座標點 (0.4, 0.35) 所代表的結果), 我們會看到三個數據 (也就是過這個點做 X 軸的垂直線, 它會被切成三段) 分別代表支持 (0.35) 反對或廢票 (0.05) 未投票 (0.6)。 要如何去詮釋這三個數字, 那是另一個問題。 本文沒有討論這個問題, 所以一開始沒把這條線段畫出來。 這當然是值得談的問題; 但是 「探討所有可能性時, 觀察到平面被切成兩塊」 跟 「有了一個座標點之後, 線段被切成三段」 這兩件事請不要混為一談。
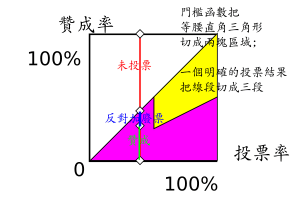
再來有讀者提到: 憲法 不也有類似的規定嗎? (例如彈劾正副總統、 變更國土) 是的。 所以我們的憲法有某些 (兩段式) 條文的數學也不及格。 (求教: 不知道其他國家有無類似的數學不及格投票法?) 但是我要幫憲法說幾句話。 (這並不表示我認同憲法的高門檻, 只是在說明憲法的數學不及格比公投法的數學不及格稍微情有可原一些。) 首先, 兩者都面對相同的困難: 如果堅持必須有高門檻, (A) 就不可行了; 但 (B) 跟 (C) 抗議的聲浪又會很大。 至於 (D) 跟 (E), 請試著用法律文字寫寫看… 我寧可用組合語言撰寫繪圖軟體還比較有趣。 但是憲法裡面那些條文適用於人數僅僅一兩百人、 受公民委託有義務出席投票的立法委員; 而公投法適用於全民 — 不投票並沒有法律責任。 再來就是上面所說的: 人數越多, 這個斷層的荒謬越明顯。 公投法選擇既不去面對 (A) (B) (C) 的民意辯論挑戰, 也不去面對 (D) (E) 的法律文字挑戰, 是極不負責任的。
[※ 3/7 補充: 給繼續支持 F 的讀者 — 如何有效挑戰本文?]
持續看到一些挑戰本文的留言, 但很遺憾都沒有抓到重點, 其中很多還是圍繞著民主的定義、 門檻的高低等等。 我來做個比喻吧。 請想像大家要去爬山, 有些人認為稜線風景比較好, 有些人認為河谷風景比較好。 先前因為某些因素, 已決定了一條路線 F; 但稜線河谷的爭議還是沒有止息。 然後某甲畫了一張地圖, 指出: 路線 F 很累人又很危險的, 一下爬高一下又掉下河谷裡面, 換一條吧! 這時繼續談論 「風景好的定義是…」、 「地圖看不出好風景…」、 「一定要多走稜線才合理啦」 都無法說服大家繼續支持路線 F。 要說服大家忽略某甲的言論, 說服大家繼續支持路線 F, 有兩個可行的嘗試方向: (1) 指出地圖畫錯了; (2) 解釋為什麼路線忽高忽低並不是問題, 甚至是好事。
我想不出來 (1) 該怎麼做; 但 (2) 倒是有一個很明確的方向: 如果你能解釋為什麼 (F) 比 (B) 合理, 或至少跟 (B) 一樣合理, 那就能夠切重要害, 反駁本文的核心論點。 看清楚了嗎? 本文沒有要挺 ABCDE 當中特定哪一個的意思; 本文的重點是在打 F。 本文不是說應該拿掉門檻, 或門檻應該降到多低才合理, 而是說: 即使拿相同的高門檻方案來比較, 單調遞增的 (B) 也遠比造成兩大荒謬的 (F) 要合理得多, 有什麼理由鑽牛角尖堅持一定要用 (F) 而不支持更簡單的 (B)? 沒有回答這個問題的挑戰, 都只是在 打稻草人 而已。
(本文轉載自 資訊人權貴ㄓ疑)