- 作者 / 艾佛瑞德 S. 波薩曼提爾、蓋瑞.柯斯、丹妮耶爾.索羅.維葛達默、凱瑟琳.基芙—柯柏曼
- 譯者 / 謝雯伃
許多心理因素會影響一個人有效且有效率地解題的能力。在前言中列出來的大多數因素(像是集中的專注力與計畫)牽涉到複合的心智歷程;你可能已經擁有這許多心智元素,卻仍在解題上遇到困難。你可能會想,還有什麼因素在阻礙你?這就是何以我們現在要討論的原因—在阻礙我們解題能力上有一個重要的因素,那就是焦慮。
何謂焦慮?
你可能對於焦慮這個詞很熟悉,那是涵蓋擔心及緊張感受的複雜感受,通常伴隨著諸如肌肉緊張、呼吸和心跳加速以及慌張的生理症狀。在某些例子中,我們能適應這些焦慮,比如說不知道能上哪所大學的焦慮,通常有助於激勵學生努力讀書取得好成績。另外,對於陌生人的恐懼,通常能阻止兒童與不認識的大人說話,讓他們避開可能危險的情況。
然而,也有許多時候,焦慮讓我們對一點也不危險的情況感到恐懼。在這些案例中,焦慮會造成人們產生負面信念並導致人們選擇迴避。舉例來說,如果有人對於公開演講感到焦慮,卻在工作場合或學校中被要求進行演說,他或她可能會對這次演講產生了負面想法。這人可能會想:「如果我犯了錯或忘詞了,那該怎麼辦」、「我聽起來可能很蠢」或是「我不知道我能不能做到」。他或她可能會汗流不止或暈眩,可能心跳加速或換氣過度。這人可能會有衝動打電話請病假或是請他人進行簡報。這些狀況都是出於焦慮,而這人若在像是算數學(被稱為數學焦慮)及解決日常生活問題的狀況下感到焦慮,這些症狀通常也會出現。

許多人與數學焦慮搏鬥,而影響了他們在這一科的表現。雖然數學焦慮根源於不理解眼前的素材,卻也因為人們想要「擅長數學」所承受的巨大壓力而生。
如果「擅長數學」會讓一個人變聰明,那麼反過來數學不好就暗示了我不夠聰明。這會帶來很大的壓力!
有數學焦慮的人通常會在面對數學題時感到驚慌,這讓他們的心跳及呼吸加速,讓有效率、能解出題目的思考被焦慮的想法給取代了。他們可能會認為「我做不到」、「我做得超差」、「這對我來說太多了」或是「我永遠都不會懂」。由於這樣多焦慮的想法不斷冒出來,難怪有數學焦慮的人在解題上會遇到困難!他們通常無法專心在問題上,往往得仰賴他人提供一步接一步的指示。有數學焦慮的人往往會不惜一切代價避開數學。兒童及青少年可能會逃學,大學生可能會避免選修數學課,而成人則可能會請朋友在餐廳「算出分攤的金額」,或是在工作時請同事協助完成基本計算。這些想避開數學的企圖在當下能讓焦慮降低;然而它們只是權宜之計,無法長期幫助一個人處理他或她的焦慮。此外,避開數學可能會讓人錯過學習解題必備的相關技巧,減少個人對概念的理解,隨之增加個人對數學的焦慮。雖然你可能會認為避開數學能減低你的焦慮,但這麼做長期下來卻可能增加你的焦慮。避開數學的權宜之計幾乎總是會產生反效果。

簡單提醒大家:不要被那些自認對數學不擅長的人給欺騙了。
如前所述,焦慮的一個關鍵元素就是迴避。如果一個人使用「對數學不擅長」作為永遠不需做這件事的藉口,他或她既避開了失敗,也因此避開向他人及自己證明他或她已經失敗的狀況。雖然像這樣的陳述可能只是拿自己開玩笑,但背後通常也有想要迴避數學的重要因素。
採取行動來減少焦慮,並以信心來取代焦慮,這對成為一個更好的解題者來說十分重要。若你本身想透過信心來取代數學焦慮,本書提供的策略將更容易為你所用。然而,你可能會對自己說:要變得自信,那可是說的比做的容易。那麼,本章會讓你知道,減少焦慮的基本策略能幫助你增加對自己的信心, 也會幫助你減少不舒服的焦慮感及身體感受。準備好你自己; 如同在本章其餘部分看見的,克服焦慮最好的方式就是面對你的恐懼。準備好「赴湯蹈火」了嗎?等結束這一段路到另一端時,想必你會對自己的能力更有信心!
在這一小節,我們會教你對於解數學題目以及解決日常問題更有信心的策略。信心並不只是「這個我做得到」的態度, 而是由某些因素所組成,包括:理解問題目標及變因、以客觀開放的心態處理問題,以及感覺準備充足並感覺自己能處理問題。
或許,信心最大的指標是一個人面對失敗的能力,因為失敗通常是不可避免的。
本章會著重在如何讓你自己準備好、感覺自己能解決問題並處理失敗。我們的希望是,在你讀完這本書後,你能具備所有能增進你解題能力的工具。
讓我們看一下以下這個問題,它乍看之下有些嚇人,但透過找出模式的策略,這個問題變得相對容易。這種讓人大開眼界的事件確實有助於建立信心。以下問題是要你找出前二十個奇數的總和。
透過檢視問題,你會發現第二十個奇數是 39。因此,我們希望找出 1+3+5+7+⋯+33+35+37+39。你的第一個反應可能是從1到39確實將它們一一相加。然而,這個方法既累人又耗時,還有無數個出錯的機會。
如同在前面章節所提到的,當你的解題經驗增加時,你解題的信心也會增加。破解這道題目的一個方法是依循稍早提到的高斯法,也就是將二十個奇數按 1, 3, 5, 7, 9, ⋯ , 33, 35, 37, 39 這樣列出。現在,注意到第一個數字和第二十個數字的總和是 39+1=40,第二個數字和第十九個數字的和也是 40(37+ 3),以此類推。接著,只需要判斷要將幾個 40 相加;既然我們考慮的是二十個數字,所以會有十組,我們接著以 10×40= 400 得出了答案。經驗這個意想不到的技巧,會讓你增加更多自信。
我們可以透過另一種模式來檢視這個問題,自然所使用的方法也不同:

這個表格明白顯示出,前 n 個奇數的總和是 n2。因此,我們問題的答案就是單純的 202=400。解題的替代方式能讓你未來的解題功力大大提升。
再舉一個例子。以下問題看起來令人困惑,難以解答。此處重點在於釐清困惑,用合理的方式來表達。
如果 A 蘋果值 D 美元,同樣價錢的 B 蘋果值多少美分?
處理這個問題的方式可以有好幾種。最常見的狀況是,選擇用數字來取代字母,然後試著重新代入字母來找出答案。不過,這很容易讓人會造成混淆,然後不幸地帶來不正確的答案。有些人可能會先尋找單位成本,然後從這點出發。同樣地,這也可能帶來混淆。
作為基本規則,類似問題的最佳解方是以某種有意義的形式來組織數據。此處,我們會利用到比例及一些常識。比例的取得,可透過設定每一分數當中同樣測量單位的數量而得出:

要注意,最後一個分數是透過常識得出的。因為這問題要求的答案是以美分而非美元來表示,這樣一來,當我們算出 x 之後,我們就找出答案了。剩下的只有簡單的計算:
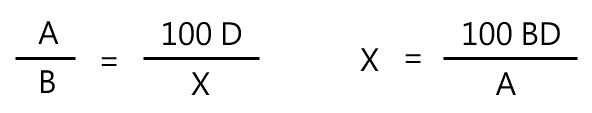
雖然經歷過這類題目,有助於我們更快速地想出這個簡單解法,但缺乏自信卻會阻礙我們停下來思考該如何以全新方式來框架問題,還可能以「繞遠路的方式」來解決問題。因為我們欺騙自己的大腦,把這些問題想得比實際上更困難。因此, 我們需要瞭解如何增加信心,好讓這些問題不會經常發生。