誰能佔領搜尋結果第一名？從 PageRank 網頁排名演算法談起

在 Google 的搜尋結果裡面，你的網頁會出現在第幾頁？被大眾看到的機會有多高？

在 Google 搜尋引擎中，有多項重要演算法來協助搜尋引擎的運作，其中，名為「PageRank」的演算法可說是關鍵中的關鍵。

PageRank 演算法已問世二十餘年，至今仍是 Google 於搜尋結果頁為網站劃分排名的核心依據之一，接下來，本文將一一簡介 PageRank 的發展及歷史、運作原理，以及它如何影響使用者所看見的搜尋引擎結果排名。

PageRank 演算法至今仍是 Google 於搜尋結果頁為網站劃分排名的核心依據之一。圖／Pexels

什麼是 PageRank ？

1990 年代，網路世界剛剛起步，搜尋引擎遠不如現在精確及貼近人心。1997 年，為了提升搜尋引擎的搜尋品質，兩位 Google 創辦人 Sergey Brin 及 Larry Page 設計出了 PageRank 演算法，幫助使用者更有效率地找到能解決問題、實用的資訊。

PageRank 的核心概念是利用網站和網站間的連結 (link) 數量多寡與連結來源的品質，來判定一個網站的價值高低，以及其在網路世界中的權威性。

PageRank 的設計靈感來自學術界對論文的評估依據之一：越多人引用的論文，表示其內容的可信度越高、品質越好，在學術界的地位越重要。同理，越多網站願意引用、放置連結連過去的網站，表示其內容越受信賴，是個值得被使用者閱讀、能為使用者帶來實用幫助的優質網站，必須排在前面、優先被使用者看到。

起初，所有人皆可透過 Google 官方開發的專屬工具查看某個網頁的 PageRank 分數，並且將 PageRank 的分數當作 SEO 評估的重要指標。

但也正因為一切分數所見即得、高低明瞭，引來有心人士濫用，利用一些投機手段在分數高的網站硬塞入自己的網站連結以獲得高分，或是將連結作為買賣交換的商品、嚴重影響公正性。

2016 年，Google 官方宣布不再公開 PageRank 分數，以解決濫用亂象。然而，雖然 Google 隱藏了分數，但 PageRank 仍然是 Google 演算法中的重要骨幹且不斷修正漏洞、持續優化中！這一點已獲得 Google 內部負責維護良好搜尋體驗的網站管理趨勢分析師 (Webmaster Trends Analyst) Gary Illyes 兩次證實。

有多少人推薦你的網站？看反向連結！

在了解 PageRank 的運作之前，必須先明白「反向連結」(Backlinks) 及「外部連結」(External Links) 的意義。

「反向連結」指的是「他人網域中，連到我的網站的連結」，而對他人來說，這是他網站中的「外部連結」，也就是「由某網域連到另一個網域的連結」。

例如，小美在她的網站裡放了一個連結導到我的網站，對小美而言，這是一個外部連結；對我而言，則是一個反向連結。

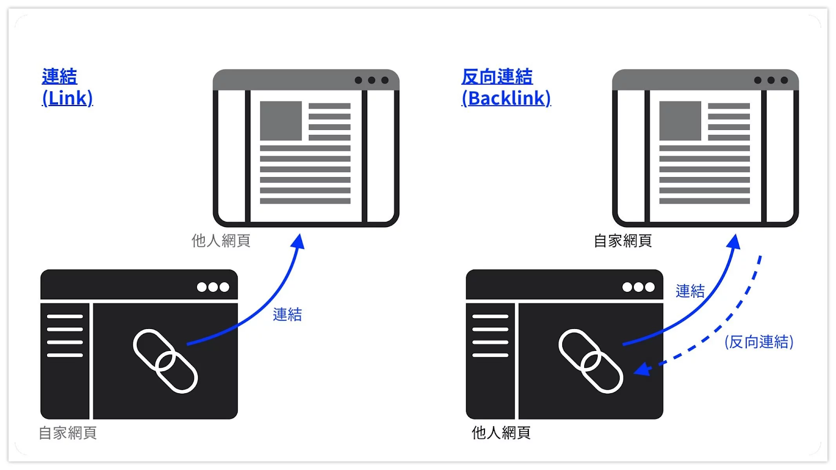
「反向連結」是 PageRank 考量的重要依據。如同前面所說的，當你的網站獲得越多反向連結、意味著你的內容被越多人引用及信賴；且 PageRank 的分數是可傳遞的，而反向連結就是傳遞的媒介。

總的來說，PageRank 會參考三項關鍵因素：

反向連結的數量以及連結來源網頁的品質
連結來源網站的外部連結數量
連結來源網站本身的 PageRank 分數

除了可傳遞性外，PageRank 運作的另一個重點是：分數會被連結對象所平分。

假設有 A、B、C、D、E、F、G 五個網頁。其中，A 是一個 4 分網頁，連結到 C 與 D；B 是一個 2 分網頁，連結到 C、E、F、G。五個網頁間的 PageRank 計算如下：

C：獲得來自 A 的反向連結並與 D 平分分數，先得 4÷2=2 分，再加上來自 B 的反向連結並與 E、F、G 平分分數，再得 2÷4=0.5 分。最後為 2+0.5 = 2.5 分。
D：獲得來自 A 的反向連結並與 C 平分分數，得 4÷2=2 分。
E、F、G：獲得來自 B 的反向連結並平分分數，各得 2÷4=0.5 分。

（補充：以上是 PageRank 的簡易算法，更完整的計算方式詳見 WiKi。）

買連結來連向自家網站，不行嗎？

你有沒有看過充滿各種無意義連結的部落格？或是專門在別人文章留言並貼上一堆無意義連結的帳號？

由於反向連結是 PageRank 計算的關鍵，在過去 PageRank 分數仍公開、被濫用的年代，許多人會刻意到高分網站洗留言、拼命留下自己網站的連結，藉此「強制」獲得 PageRank 分數；又或者，高分網站開始兜售反向連結，浮濫連去各式各樣客戶的網站。

隨著 Google 的反制，大量洗連結、買賣連結等手段已經被明文禁止，也有相應的其他演算法來偵查這些惡意行為。像是企鵝演算法 (Google Penguin) 就是 Google 用來掃蕩植入劣質反向連結網站的演算法。

有趣的是，Google 自家的 Chrome 瀏覽器也曾經違反自家的規定而被懲罰，2012 年時， Chrome 因付費購買不當連結來行銷自己，對此 Google 除了公開道歉外，還將 Chrome 原先在搜尋結果第一頁的排名大幅調降，長達兩個月之久，而此事件也因此成為了 Google 反制劣質連結的經典案例。

別讓自己淪為人人喊打的黑帽 SEO！

洗連結這種欺騙搜尋引擎的作弊手法，在搜尋引擎優化 (SEO, Search Engine Optimization) 技術中被稱為黑帽 SEO (Black Hat SEO) 。

使用黑帽 SEO 雖然可能在短期內快速取得 SEO 成效，但正如上述所提，黑帽手法違反搜尋引擎的規範，所以如果使用黑帽 SEO 且被演算法發現，後果將會不堪設想！除了洗連結和買賣連結等，在文章中硬塞關鍵字也是黑帽 SEO 的一種。

補充：更多黑帽SEO手法介紹可以參考美國SEO權威網站MOZ

雖然 PageRank 演算法仍然是 Google 進行網頁排名的命脈之一，但如果網站經營者想提高自己網站的 PageRank 分數，最好的辦法還是打造出優質的網站內容，獲取其他高分網站的認同與信賴、願意在他們的網站中放上你的連結，爭取到高價值的反向連結！

參考資料

本文轉載自中央研究院研之有物，泛科學為宣傳推廣執行單位。

採訪撰文｜郭雅欣、簡克志
美術設計｜林洵安、蔡宛潔

在學術與搖滾的多重維度上行走

還記得美劇《The Big Bang Theory》嗎？劇中常常出現的物理名詞「弦論」，是描述物理世界基本結構的理論。中央研究院「研之有物」專訪院內數學研究所程之寧研究員，她正是研究弦論的科學家，也是熱愛音樂的搖滾樂團鼓手，這種跨領域身份並不衝突，兩邊都需要創造力與紀律。由於天生斜槓的性格，讓程之寧在數學和物理領域大展身手，透過數學的深入探討，她試圖將弦論更往前推進。最近程之寧更跨足到人工智慧領域，為學界提供理論物理上的貢獻。

中研院數學所程之寧研究員，主要研究 K3 曲面（特殊的四維空間）的弦論，她發現模函數和有限對稱群之間有 23 個新的數學關聯，稱之為「伴影月光猜想」（Umbral Moonshine）。圖／研之有物

萬有理論和難以捉摸的「月光」

世界從那裡來呢？物理世界的本質是什麼呢？回答這樣的大哉問，一直是理論物理學家所追求的目標。從牛頓力學（日常應用）、廣義相對論（探討很重的物質）到量子力學（探討很小的物質），隨著物理學不斷發展，我們似乎一步步接近答案，但至今卻還未走到終點。

舉例來說，如果有個東西很重又很小，就像「黑洞」，或是大爆炸時的宇宙，我們要怎麼用數學描述？於是科學家試圖整合廣義相對論和量子力學，找出所謂的「萬有理論」（Theory of Everything）──能完全解釋物理世界基本結構的核心理論。

程之寧研究的「弦論」就企圖發展成這樣一個萬有理論。弦論一如其名的「玄妙」，它設定宇宙所有的粒子都是由一段段「能量弦線」所組成，每一種基本粒子的振動模式不同，產生不同的粒子特性。

「人類一直以來的夢想之一就是，如果能用一句話解釋所有事情，那該有多麼美好。」中研院數學所研究員程之寧說道。

程之寧的研究牽涉到數學上的「月光猜想」（Moonshine）與弦論中 K3 曲面的連結。月光猜想是存在於模函數係數與特殊群之間的數學關聯，程之寧與其研究夥伴共發現了 23 個新的關連，並稱之為「伴影月光猜想」（Umbral Moonshine）。

基於弦論的假設，我們的世界是十維的，除了人們在日常生活中可以感知到的 3+1 維（空間＋時間），還有六維是因為尺寸太小而無法用肉眼觀察的，這些看不到的維度影響著物理世界，最終也產生了我們這個物理世界所需的各種條件與特性。

綜觀程之寧的研究，橫跨了物理與數學兩個領域，她笑稱自己「天生斜槓」。在學術上，程之寧原先喜歡文學，之後卻走上數理研究的道路；在音樂上，程之寧喜愛搖滾樂，至今仍在自己的樂團裡擔任鼓手。

她如何看待自己一路走來的各種轉折？游徜在數學與物理之間，她又對這兩個領域的連結有怎樣的體會？在與「研之有物」的訪談中，程之寧侃侃而談她的經歷、想法，以及對學術研究的熱忱所在。

在弦論的設定中，宇宙所有的粒子都是由一段段「能量弦線」所組成，每一種基本粒子的振動模式不同，產生不同的粒子特性。圖／iStock

請問您是如何對數學及物理產生興趣？從何時開始？

一開始考大學時，其實我想去念中文系（笑）。不過，因為我高中是選理組，而且只念了一兩年，對文科考試比較沒把握，加上對工程科系沒興趣，最後就選擇臺大物理系就讀。

後來發生兩個轉折，第一個是我很認真的去修了大學中文系的課，結果發現真的沒有想像中容易。第二個就是我發現物理系的課還蠻有趣的，像量子力學和相對論，讓我覺得還想再多學一點、多知道一點。

我開始覺得如果念完臺大物理系就停下來，好像有一種小說沒讀完的感覺，所以就想繼續讀碩士班。那時還沒有覺得自己會走上學術研究的路，單純抱著想把故事看完的想法。

後來是如何接觸到弦論？弦論是如何引起您的興趣？

後來我去荷蘭念碩士，指導教授是諾貝爾物理獎得主 Gerard ’t Hooft。他其實蠻不認同弦論，但他對於如何處理量子力學與相對論很有興趣。

當時 ’t Hooft 教授在建議我碩士題目時就說：「你也知道我不太認為弦論是一條正確的道路，不過聽說弦論最近真的在量子重力這一塊有一些成果。不如妳去讀一讀，看看是不是真的有一些東西在那裡，也可以比較一下其他量子重力理論。」

在我很認真的比較各個量子重力理論之後，就變成弦論派了（笑）。’t Hooft 教授對此也保持開放態度，他有幾個不錯的博士生後來也變成弦論學家，之後我在 Erik Verlinde 的指導下念博士時，就完全以弦論為研究主題了。

研究理論物理會影響您對現實世界的理解嗎？

蠻多人會問我說，妳學了量子力學，是不是就會比較了解這個世界不是非黑即白？或問我量子力學跟宗教是不是有關？可是我覺得我分得很開，我不會去做這樣的連結，我還是活在現實裡，走路時大部分都在專注於自己不要跌倒之類的。

如果真的要講，我蠻感激我們的存在，因為我所學的東西讓我知道這是沒有必然性的。我們能這樣以一種人形的很奇怪的生物的形式存在，然後在這樣一個環境過一輩子，是機率很低的事情，而且我還蠻開心我是當人，而不是奇怪的阿米巴蟲或外星生物！有些人會從這裡連結到宗教或轉世，但我不會，我就停在這裡。

來談談您的研究，伴影月光猜想與 K3 曲面弦論之間是什麼關係？

弦論中有很多的可能性，我們可以挑選特定的四維，然後假設這四維空間是個 K3 曲面。例如說，我們可以把兩個甜甜圈乘起來，在上面做特殊的奇異點，來製造出一個 K3 曲面。這個曲面有一些很有趣的對稱性。從弦論的角度來講，我們可以透過這個過程，找出一個解釋為何有伴影月光猜想的框架。

「把維度乘起來」這個概念很難想像，但這在數學上是成立的。我舉例一個我們能想像的「乘起來」：如果有一個空間是一條線，另一個空間是一個圓，乘起來就變成一個圓柱形，從一個方向剖面可以切出圓，另一個方向則切出線。而在數學上，不管幾維，能不能在紙上畫的出來，都可以這樣操作。

如何透過計算，發現捉摸不定的「月光」？

有時候這看似湊巧，一個數學上的函數正好就是弦論某個問題的答案。但其實並不是真的那麼巧，弦論看起來很有彈性，好像什麼都可以解釋，但它其實有非常多結構及限制。

當我在計算一個弦論理論時，它的內部結構可能原本就具有某些特定的性質，然後我再去觀察數學中，有這樣性質的函數可能就只有一兩個，只要再初步算一下，就能知道哪一個是答案。弦論學家日常的計算常常是這樣的，所以這是巧合嗎？是也不是。

您曾經發現 23 個新的伴影月光猜想，您對這類題目特別有興趣嗎？

我覺得數學有兩種，有些數學家喜歡系統性的事情，就像蓋房子一樣，在數學裡建造一個很美麗、非常有系統性的結構，可以把很多事情都放入這個結構來理解。

另一種比較少數的，就是喜歡獵奇，去收集分類奇奇怪怪的特殊東西，例如有這些性質的函數在哪裡？可能你算出來就是 5 個，你也不知道為什麼。月光猜想很明顯就屬於這一類。

兩種的樂趣感覺是不一樣的，我覺得應該都很棒，但我可能是屬於偏好獵奇的這種。

您的研究連結了物理上的弦論與數學上的月光猜想，您怎麼看待這兩個知識體系的互動？

弦論是一個需要很多數學理論配合的物理理論，它是一個有點繁複的框架，我們什麼都要會一些，才能看懂這個理論。當你把許多不一樣的學門的知識加起來，有時候就會在某一個學門──例如幾何──有意想不到的收穫。

弦論在數學上也扮演探索與找尋新方向的角色，讓數學家有新的發現。雖然最後數學定理的證明還是得仰賴傳統數學方法，但在這二三十年間，我們一直從弦論身上找尋數學研究的新方向或有趣的猜想，看到了弦論與數學之間的互動。

數學家有兩種，一種人喜歡建立美麗又有系統性的結構，另一種人喜歡尋找和收集奇怪特殊的數學物件（比如函數），程之寧表示自己屬於後者。圖／研之有物

剛才一開始提到，您高中只念了一兩年，是因為對學校沒有興趣嗎？

其實我一直都覺得上學很無聊。我小時候臺灣教育和現在很不一樣，一班 50 幾個人，老師必須盡量軍事化管理，大家最好都一模一樣，比較好管理。我和學校一直處於互相磨合的狀況，我自認已經努力配合學校，但學校一直覺得我在反抗，這可能是一個認知上的差別。

舉例來說，我小學的時候不想睡午覺，可是老師說大家都一定要睡午覺，不睡午覺的人要罰抄課文，所以我早上到學校時就會把已經抄好的課文交給老師。我覺得我這樣做是在配合老師的規定，可是以老師的立場會覺得我在反抗，學校教育中我遇到了很多類似的情況。

還有就是不喜歡高中的升學氛圍，同學和老師好像都只有一個活著的目標，就是「考大學」。我當時無法習慣升學氛圍，感覺好像活在平行宇宙一樣。

高中休學後，您去唱片行工作，可否談談當時的想法？

我國中開始聽音樂，這是我除了看書之外的重要興趣，我也很快就喜歡上了搖滾樂。高中休學的時候，我唯一的謀生技能可能就是我對音樂的各類知識吧！所以我就去了唱片行，這是唯一一個我會做又有興趣的工作，還好那時候還有很多唱片行（笑）。

對音樂的熱忱，讓您與朋友共組了樂團，並擔任鼓手。您是否比較過樂團生活和學術研究之間的異同之處？

有些人覺得我這樣很跳 tone，但我自己覺得還好。音樂和學術都是我發自內心覺得好玩的東西，兩者也有相同之處，例如它們都需要創造性，也都有需要了解的框架。數學需要嚴謹的證明，音樂演奏也需要遵循結構，例如不能掉拍。

音樂領域還有一點和數學類似──玩樂團的圈子也是以男性為主。我們樂團則是只有一個男生，其他都是女生，可能我真的天生對框架有點遲鈍，玩團之後才發現：「怎麼大家都是男生？」

也就是說，目前數學學術圈仍是男性主導，在研究路上，您有因為性別而感受到一些衝擊或眼光嗎？您怎麼面對？

有。那感覺很明顯，日復一日地要去面對，尤其是年紀還比較輕、還必須每一天去證明自己的能力的時候，特別有感。

我遇到時的反應就是，在心裡暗罵一句髒話，然後繼續做我要做的事。我不會想改變別人的想法，感覺那是浪費時間，就算環境給我的阻礙是這樣，我還是繼續去做該做的事。

可是有些事情沒那麼簡單，現在我也當過老師，有時候會看到年輕女生在學術界因為性別而被欺負，或遭到不公平待遇、甚至騷擾。

對此我感到心痛，覺得為何我們學術領域還是這樣的狀況？甚至為什麼性騷擾至今還是一個議題？可以確定的是，學術界許多性別不平等問題未受到重視。

您現在已經有傑出的研究成果，還會因為性別而遭受質疑嗎？

我現在比較會遇到一個狀況反而是來自學生的質疑。我在荷蘭阿姆斯特丹大學教書時，有時候學生會因為我是女教授，而且我的外表在許多歐洲人眼中看起來就像小妹妹，所以比較容易去挑我的毛病。

在課堂上，下面坐的可能都是男學生，只有一兩個女學生，那個氣氛就會變得很奇怪。例如說偶爾會聽到學生評論我的身材或樣貌。

我有和其他一些在歐洲或美國的女性教授聊過這樣的問題，似乎不少人都有類似的不太愉快的經驗。感覺不是很好。

看到您最近的研究和人工智慧（AI）有關，為何會想往這個方向發展？

我有兩個動機。一個就是我真的想深入了解人工智慧。我也可以像普羅大眾，看看 AI 下圍棋，讚嘆「哇！好厲害！」這樣就好，可是我覺得我一定可以真的去理解它，這可能就是數學家的自大吧！

另一方面，我知道對科學研究來說，未來 AI 將會是一個非常重要的工具。這是「在職訓練」的概念，我可能會用到這個新工具，或以後我可能會需要教這樣的課，因為學生是下一代的科學家。因為這些原因，我覺得我需要去訓練自己使用新的工具。在我的領域裡，也有一些有趣的、還沒被解答的科學問題，是 AI 有可能幫得上忙的，我看到了一些潛力。

弦論和 AI 感覺差距很大，AI 也可以應用到弦論的研究嗎？

乍看之下，弦論的確比較抽象，也不像其他許多實驗會產生大量數據。但其實弦論有大量的可能性，我認為使用 AI 來在這些巨量的可能性當中搜尋特別有趣的理論，是一個有潛力能夠加深我們對弦論理解的新的研究方法。

而且 AI 的應用絕不僅限於巨量資料。如果是面對一些比較新的挑戰，在沒有現成的演算法可以用的情形之下，可以自己做出需要的功能嗎？這過程我覺得也非常很有趣，而且應該是會有成果的一條路。這種不是那麼顯而易見的事情，我覺得很有挑戰性，也蠻好玩的。

除了用 AI 來幫助物理跟數學的研究之外，我也試著物理研究當做靈感來源，找出新的 AI 的可能性，我覺得這也是一個很有趣的研究方向。我現在有和 AI 的學者合作，嘗試做出一些創新的演算法，真的還蠻有趣的。

AI 對您而言是全新的領域，您如何面對跨領域遇到的門檻？

一開始會覺得真的要去碰這個新的領域嗎？其實現在也還是偶爾會有這樣的懷疑。我在弦論領域可能已經是專家，但去了一個新的領域，我學得不會比二十歲的人快，要怎麼去跟人家競爭？是不是在浪費時間？

但也會想，與其想這麼多，不如先做再說。到目前為止我做了兩年多，感覺還蠻好的，我有學到東西，也有做出小小的貢獻。

其實我還蠻感激有這樣的學習機會。對我來說當科學家最大的好處就是，去搞懂一個新的東西就是工作的一部分。當科學家雖然蠻辛苦，但就結果論來說，我還蠻開心能當一位科學家！