作者 / 單維彰 │ 國立中央大學師資培育中心與數學系合聘副教授
y編按:108 數學領綱中很重要的革新項目之一便是將「計算機」這個「微小而又謙卑的工具」,引入國中及高中階段的數學教育中;而在考試的部分,也研擬能「准用計算機」,此話題引起了討論,甚至有人認為此舉太過「理想主義」。
香港的大考制度和台灣不同,在他們的數學考科中,已經能准用計算機;實際上的使用方式為何呢?推動者又怎麼看這樣的轉變?讓我們一起來從今日的香港考制,來看看明日台灣。
在這段日子裡,我們特別關心香港同胞;七月也是臺灣的傳統「考季」,而此時國內聚焦的教育議題之一,正是今年 8 月的數學新課程開始使用計算機之後,將來的數學學測與分科測驗,是否也該准用計算機?
我們就一起從這篇文章開始,來看看香港的數學大考如何使用計算機吧。
香港的大考長什麼樣子呢?
香港以前的教育制度大致與英國相仿,採用英國版的標準化測驗作為中學畢業的學科能力評量。成為中國的特別行政區之後,教育事務屬於港人自治的範圍,其學制逐漸從英國規格轉換為 6-3-3-4 制*,使得香港的學制與其周圍鄰國一致,包括臺灣、中國、日本和韓國。
- 編按:即是小學 6 年、國中 3 年、高中 3 年、大學 4 年的學制。
相當於我國高中畢業生參加的學測與指定科目考試,在香港稱為中學文憑考試(文憑試,DSE:Diploma of Secondary Education)。而泛稱「劍橋考試」的各級標準化評量,也改由香港考試及評核局(考評局,Hong Kong Examinations and Assessment Authority, 簡稱 EAA)主辦;EAA 相當於我國的大考中心,它們都是財務獨立的法人機構,不過實務上仍有諸多不同之處。比如說考試費用計算方式:以相當於學測的數學考科為例,香港的應屆畢業生,由學校團報的報名費是 448 元港幣,直接兌換約為 1800 元台幣;而臺灣的報名費僅為 200 元。考試的時間也有所不同,香港的考試時間是 210 分鐘,臺灣只考 100 分鐘。
而考試又考些什麼呢?香港文憑試提供四個核心科目:國文、英文、數學(必)、通識教育,它們的角色相當於我國的學測。此外,文憑試提供高達 24 個選考科目(其實不只如此,但是詳情不及備載),包括兩個數學選考科目:數學(一)和數學(二)。因為整個考季長達一個月,各門考科不相衝堂,所以各方學霸盡可挑戰大滿貫。可是,香港社會已經脫離了考試崇拜的幼稚期,以 2018 年的 5 萬 5 千多名考生為例,70% 的考生選考二科,16% 選考三科,8% 僅選考一科。
選考科目之中,考生最多的前五名是:生物(14500 人)、化學(14000 人)、經濟(14000 人)、物理(12000 人)、地理(10000 人)。想請讀者特別注意的是:香港還存在像是「經濟學」之類的選考科目,而且相當熱門,反觀我國甚至連這一門選修課程都沒有。而選考數學(一)和數學(二)的人則並不多,依序擁有 2900 名和 5200 名考生。
筆者特別想要指出:香港文憑試的「通識教育」考科是一個非常有創意的評量設計,非常值得我們注意。但是本文專注於數學,在此先忍住不發,或許未來有機會再跟各位聊聊。
數學考科如何准用計算機?
香港考評局出版一份〈准用計算機型號名單〉文件,列出十三種品牌將近四百種機型,每一種都會在機殼上顯示 HKEAA APPROVED 標誌。在香港的書局裡,幾乎都可以看到一個專區,陳列合格的計算機商品。香港文憑試的三種數學考科,全都准用計算機。而攜帶合適的計算機應考,是學生自己的責任。

數學(必)分成兩段考試,卷一考 135 分鐘,占 65 分,全是需書寫過程的非選題;卷二考 75 分鐘,占 35 分,全是單選題。選考的數學(一)和數學(二)各考 150 分鐘,全是需書寫過程的非選題;其中數學(一)的試卷提供正規分布表,數學(二)的試卷提供三角公式(如下圖)。
所謂「准用計算機」的概念是,學生只要認為有需要,就可以用。有些概念性的問題,計算機應該是幫不上忙的,讓我們從 2018 年的「數學(必)一」試卷來一起感受一下。例如:
1.化簡 \(\frac{xy^7}{({x^{-2} y^3})^4}\) 並以正指數表示答案。(2018試卷一2)
2.將 265.473 捨入至二位有效數字。(2018試卷一3(a))
有些試題需要基礎的計算能力,考生可以根據自己的能力而決定是否適合使用計算機,例如:
3.某物的標價較其成本高 30%,已知以其標價六折售出虧損 88 元,求該物之標價。(2018試卷一7)
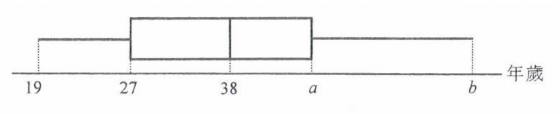
4.參閱下圖,已知全距為 43、四分位距為 21,求 a、b;這是題組的第 1 小題。
第 2 小題接著問:若上圖為 X 組文員的年齡分布,另有 Y 組五名文員,其中三名均為 38 歲,且 Y 組年齡的全距為 20。如果將 X 和 Y 合併為一組,公司經理宣稱新組的年齡全距必與 X 組的年齡全距相同。你是否同意?試解釋你的答案。(2018試卷一10)
大多數的讀者大概都能心算或筆算以上題目所牽涉的計算。香港與台灣的差異在於,我們要求全體學生必須具備前述計算能力,而且必須自己算,但是他們容許學生選擇較有效率的作法。
就筆者觀察後的意見而言,香港的數學(必)試題沒有使用計算機即可直接得到答案的題目,也很少非要使用計算機否則無法算出答案的題目。就 2018 年數學(必)試卷一的 19 道試題而言,僅有以下這一題,筆者自認無法筆算,非得拿起計算機不可:
5. 某等比數列的第 3 項及第 4 項分別為 720 及 864。(a) 求第 1 項;(b) 求 n 的最大值使得第 n+1 項與第 2n+1 項之和小於 5×1014。(2018試卷一16)
以上雖然僅就 2018 年的數學(必)試卷一舉例,但是筆者觀察試卷二以及選考的數學(一)和數學(二),所得的結論是一樣的:有些觀念性的題目,有沒有計算機的差異不大;大多數的題目,僅需基礎的計算能力,部分學生使用計算機可能會提高其作答效率,但客觀而言並非必需。只有很少量的題目,看來必須使用計算機。
由於試卷上有「標準答案」的需求,所以也會特別註明關於概數的約定語言。例如,數學(必)試卷聲明:「除特別指明外,數值答案須用真確值,或準確至三位有效數字的近似值表示」,數學(一)和數學(二)也有同樣的聲明,只是將近似值改為「四位有效數字」。
當計算機成為學生的好夥伴
將計算機列為數學課程的教學目標,為的是要讓學生有機會藉由工具的協助來理解數學,進而培養對於數學的正向態度,也使得學生有機會「探究」數學。由於數學大多是抽象概念,不同於自然領域通常有實際的觀察對象,在數學教育中引進計算機,也能使得續學課在某種程度上也有機會從事觀察、實驗與探究。
長久以來在台灣,「不準使用科技工具」的教育現實,就像一片透明天花板,重重壓在每位教師和學生的頭上。眼看著科技文明不斷更新,國際同儕的教育內容不斷進步,我們卻被這片透明天花版壓制在下而無法成長。
若能讓計算機真正落實在數學課程裡,相信這個微小而謙卑的工具,會成為刺破天花板的小尖兵,改變教育領域,讓社會對於數位工具的接受度能夠逐漸改變。