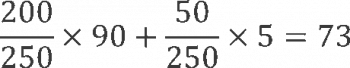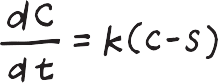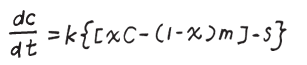第二週早上,我(小昭)刻意選擇跟上週一樣的時間去可大可小吃早餐, 但沒遇到世杰跟他的數學講義。我有點失落,以為建立起來的默契, 看來只是自作多情。我要用貝式定理來算一下得扣世杰幾分。
一走進教室,同學們散落在後方的座位聊天、吃早餐、玩手機。世杰獨自坐在第一排津津有味地讀著講義。真的很喜歡數學呢,我看著他的模樣,剛剛的失落一掃而空。他看到我,不過可能是在思考數學吧,他又低下頭,一會兒才再抬頭跟我打招呼。
「早安!」
「你原來已經在教室了。我剛去吃早餐時還在想會不會遇到你。」
「遇……遇到我嗎?妳、妳說妳想像會遇到我嗎?!」世杰臉上露出驚訝的表情,我剛剛的話太積極嚇到他了嗎?
「哈,你幹嘛裝得那麼誇張,好好笑噢。」我趕快用開玩笑的語氣回答。
他挪開椅子上畫有數學符號的背包。

「我在想一個跟咖啡有關的數學。」在我坐下後他說。
我沒預期到才三句話就進入數學的話題,就像電影開場五分鐘就主角就跟壞人生死決鬥一樣讓人措手不及。我伸手抓口袋裡的手機,思考怎樣才能在不被發現的情況下跟欣妤求助。
「怎樣的數學呢?」
「假如早上妳泡了一杯熱咖啡,冰箱裡還有一杯冰牛奶,妳想在10分鐘後喝杯涼一點的咖啡。妳有兩個選擇,先把冰牛奶倒進咖啡裡,靜置 10 分鐘。或先放 10 分鐘後,再倒冰牛奶。妳會選哪一個?」
我鬆了口氣,還好他不是要我立刻解一道方程式。是非題至少有一半的答對機率。
「我選第二個,感覺比較冰。這跟數學有關嗎?」
「有噢,溫度是可以算出來的。」
世杰拿筆寫下數學式子,我看見了 y,y 右上方還有一撇。那是什麼意思?不小心畫到的嗎?
「小昭,妳幹嘛坐那麼前面啊?」欣妤的聲音從後方傳過來。太好了,我趕快起身離開。
「欣妤學姊!不好意思,下課你再解釋給我聽好嗎。」
「就說不要叫我學姊了。他誰啊,啊,世杰嗎?」欣妤壓低音量說,我點點頭。世杰禮貌地跟欣妤打招呼後,繼續看講義。我小聲地告訴欣妤剛剛的狀況,感謝她的及時出現,否則我就要出包了。
「右上方那撇是微分啦。咖啡溫度的數學,這我有印象。妳等我問大家。」
欣妤在群組裡連發了好幾則訊息,裡面有「咖啡」、「溫度」、「微分方程」、「混合」等字眼,每一個字我都看得懂,但串在一起就變得陌生。
「妳剛剛忽然離開,他會不會受傷啊。」欣妤看著螢幕打字邊說。
「好像有點沒禮貌……可是如果繼續坐著就穿幫了。」
「不然妳跟他說下午去咖啡廳做實驗,這樣就能順理成章地約會啦。放心,我會在那之前幫妳準備好需要知道的數學知識。」欣妤抬頭看我,兩眼發亮,一副比我還期待的模樣。
咖啡廳裡的數學實驗室
「兩杯熱咖啡,再給我一份冰牛奶。」世杰從櫃檯走回來。
「這間咖啡廳很棒哎。」我們坐在靠窗座位,旁邊放了個裝咖啡豆的大麻布袋,跟椅子差不多高。
「好復古的桌椅。」
「我猜不是復古,老闆當初開店時說不定還是挑最新款式的。」世杰調皮地踩了踩地板,發出嘎嘎聲響,和老闆娘磨豆的聲音,一起融合在店裡的爵士樂裡,賦予這間咖啡廳一種獨特、經年累月沉澱出的優雅氣氛。
「世杰老師的咖啡廳數學課要開始了嗎?」
「好,妳聽過牛頓冷卻定律嗎?」
我點點頭,心想欣妤真會猜題。她只聽到咖啡兩個字,就可以猜出世杰會用到哪些數學。聽說他們還有去問世杰的同學孝和,或許孝和也幫忙給了些建議。
「冷卻定律的意思是,我們點了一杯熱咖啡,從沖泡好的那一瞬間起,它的溫度就會開始下降,下降速度跟咖啡此刻的溫度與室溫差距有關……」世杰解釋起牛頓冷卻定律,我在三小時內第二次聽到這個理論, 但對它還是非常陌生。
「你們的咖啡來了,起士蛋糕是招待常客的。」
「老闆娘都認識你,好厲害噢。蛋糕真好吃。」我挖了一小塊送入嘴中,此刻我非常需要咖啡和糖分。
「我還滿喜歡吃他們的起士蛋糕。」世杰也挖了一塊蛋糕。我原本有些擔心他眼裡只有數學,其他都沒興趣,但現在看起來應該是我多慮了。他喜歡探索自己的興趣, 同時也願意廣泛接受其他事物,回去又多一項要列入貝式定理計算的項目了。

「我大概懂你說的,溫度變化能用斜率表示,變化又跟咖啡溫度和室溫差距有關,所以可以列出等式。然後……算出咖啡從泡好開始,每分鐘的溫度變化。只是,這樣跟牛奶先倒後倒有什麼關係呢?」
我一口氣背出群組裡的大家幫我整理好的台詞。「不用講太多, 讓他以為妳數學不錯就好。剩下來給他發揮吧。」離開前欣妤這樣告訴我。把數學當成國文在唸,這對我來說不是太陌生的一件事。
世杰把冰牛奶倒入其中一杯咖啡,在餐巾紙上寫下算式,
「有噢,當冰牛奶倒進熱咖啡,假設牛奶跟咖啡的比熱相同, 熱咖啡 200 克,90 度。牛奶 5 度,50 克。混合後的咖啡牛奶就是 73 度。」
「噢~」我湊近看式子,裝出一副很有興趣的模樣。
「可以嗎?各自的比例乘上各自的溫度。」世杰補充,我心虛地點點頭。
還好世杰沒察覺出來,此刻他是數學世界的導遊,用介紹知名景點的口吻,指著加牛奶的咖啡說:「所以囉,如果先倒冰牛奶,咖啡就會從 90 度下降成 73 度,之後的 10 分鐘再慢慢變涼。還記得我們剛剛說的,熱咖啡變涼的速度,取決於咖啡和環境的溫度差。比較涼的咖啡,降溫速度會比較慢。」他邊寫邊說。
假設咖啡一開始的溫度是 C,周遭環境溫度是 s,溫度隨著時間 t 的變化是:
k 是常數。現在多了溫度 m 的牛奶,混合後咖啡占整杯拿鐵的比例是 x,則先混合後靜置的狀況,降溫的變化可以寫成:
「中括號裡面的 xC-(1-x) m 就是我們剛剛算的 73 度,咖啡跟牛奶混合後的狀況。再利用微分方程,就可以解出來了。」
Napkin Math(餐巾紙上的數學),我總以為這是只有電影裡才發生的畫面。
「你學過微分方程了嗎?」我說出阿叉在群組裡的問題。
「下學期才要修。」
「那你怎麼會?」
「因為好像還滿有趣的,就稍微翻了一下。微分方程告訴我們, 混合後的拿鐵溫度 T1 隨時間 t 的變化:
「妳研究一下,我去拿另一杯冰牛奶。」
世杰起身走去吧台,我趕快把公式全部拍到群組裡,再補上一句:
這到底是什麼?
先倒牛奶再靜置降溫的公式。
不用懂整個公式,只要記得 x 跟 (1-x) 是混合的意思,e-kt 就是放著降溫的過程。
阿叉跟商商回覆我。
我想起中午我們的確有討論過,x 是混合的比例,比方說 30% 的黑色跟 70% 的白色混合,就可以用 x 跟 (1-x) 來表示。e-kt 則是像以前理化課學的半衰期,指數上頭有個 -t,表示隨著時間減少,而且不是線性遞減,是每隔一陣子少幾倍的那種指數遞減。
欣妤補了一句:括號裡面的先算,所以是先混合,再降溫。
從他們的口中,公式變得好像一幅畫,這邊是一個花瓶,那邊是另一扇窗戶。雖然細節我還是不懂,但至少稍微能理解這個式子了。耳邊傳來地板嘎嘎聲響,世杰捧著一杯冰牛奶走回來。
晚一點倒牛奶,咖啡比較涼
「冰牛奶來囉,我就省略計算過程,第二種狀況咖啡溫度 T2(t)是:
中括號裡的是放涼一陣子後的黑咖啡溫度,然後用剛剛講的比例乘以各自的溫度,平均起來,就是先放涼,再加冰牛奶的狀況。」我看了看式子,有 e-kt 的是靜置降溫,有 x 跟 (1-x) 的是混合,括號裡面的要先算,表示事先發生的事情。
「所以這個式子的確是先降溫,然後再混合。」我覺得有點開心,我竟然可以解釋這個式子哎。世杰點點頭,把冰牛奶倒進去第二杯咖啡,邊攪拌邊說:「妳有興趣的話可以試著推導看看,可以證明不管 t 是多少, 都可以得到 T1(t)> T2(t) *,證明的關鍵在於牛奶溫度 m 比室溫 s 要小。」
「嗯嗯不用了沒關係,我相信你是對的。」世杰把杯子推到我面前。
「妳現在喝喝看這兩杯,哪一杯比較涼。」
「這杯真的比較涼哎~你好厲害!」
「沒有啦。是微分方程厲害……」世杰露出不好意思的笑容。阿叉的建議果然很中肯。
*編按:算式結論原誤植為 T1(t)< T2(t),已更正。(2019/3/12)
本文摘自《超展開數學約會:談個戀愛,關數學什麼事!?》,臉譜出版。