- 首圖圖源:《Science》
文/林子揚
國立清華大學分子與細胞生物所博士生,從事像是手工藝品一樣的植物保存研究。興趣涉及演化學、生態學、考古學和地球科學,嗜好是研讀跟自己研究題目完全無關的科學新知。
幾天前在《自然通訊》(NATURE COMMUNICATIONS)發表的論文,記錄一種在紐西蘭南島發現、年代距今約 5550~5950 萬年前的古企鵝。這種企鵝命名為 Kumimanu biceae,屬名由毛利語的 kumi (神話中的大怪物)和 manu(鳥)結合,種名是紀念主要作者的母親。

而科學家發現的這份化石,其所有的骨骼集結成一個團塊;將這個團塊拆分開來後,主要是部分的上肢骨骼(肱骨、烏喙骨、尺骨、肩胛骨)和胸椎、脛骨。雖然完整度並不算高,從這些骨骼已經可以推算大致的尺寸。肱骨整體長度大約為 18~23 公分之間(因為化石缺了一端),這個尺寸是企鵝化石物種中排前幾名的。 Kumimanu 站立時身高推估約為 1.77 公尺左右,體重約 100 公斤。而現生最大的皇帝企鵝也只有 1.2 公尺高、46 公斤重,所以可知新化石物種有兩倍左右的體重,和成年人類相若的高度。
Palaeeudyptes klekowskii, el pingüino ‘coloso’, hace 36 millones de años… pic.twitter.com/LkHeQzJvna
— Gerardo Sifuentes (@Sifuentes) 2014年8月4日
- 圖片指的只是巨型企鵝,而非 Kumimanu
讓中生代結束的隕石事件,造成非鳥類恐龍滅絕後,取而代之的巨大陸行鳥類高達 2 公尺,是當時生態系的主要掠食者,雖然牠們現存的近親們是餐桌上的雞鴨鵝。
那些也很大的古企鵝們
與這些巨鳥同時期,往海中發展的企鵝也快速地演化。企鵝這個類群是何時獨立分支還不清楚,或許在 6800~7000 萬年前的白堊紀末期,也可能是在 K-T 事件(Cretaceous–Tertiary extinction)發生後很短的時間內。不過可以確定的是,企鵝的祖先生活在南極洲和紐西蘭一帶(當時兩者之間的距離約 1500 公里,比現在近很多)。
已知最早的企鵝是約 6200 萬年前的威馬奴企鵝(Waimanu),從這個屬名和本次新物種一樣有 -manu 的字根,就知道一樣是以毛利語來命名;這個屬名的意義是「水中的鳥」。威馬奴企鵝雖然已經不能飛,但前肢還保有原為翅膀時的關節,現代企鵝則已經演化成堅挺的鰭狀構造。下面是這種企鵝的復原圖:

其實在 Kumimanu 發現以前,就已經知道早期企鵝有巨型化的趨勢,不過那是進入始新世後的事件。最為彰顯的是古冠企鵝(Palaeeudyptes)和劍喙企鵝(Anthropornis)兩個類群,牠們生活在始新世中期到漸新世早期之間,一般尺寸和新發現的 Kumimanu 相近,其中最小的物種也大於皇帝企鵝;至於最大的則是卡氏古冠企鵝(Palaeeudyptes klekowskii),可能身高達 2~2.2 公尺之間。
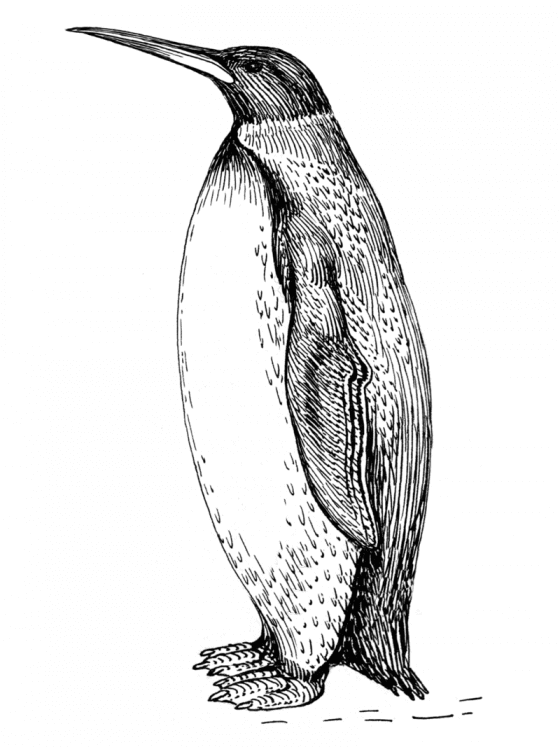
所以 Kumimanu 並非紀錄中最大型的企鵝。但值得注意的是,牠是年代最早的巨型企鵝,而且出現的年代只比威馬奴企鵝晚一些,約在古新世中晚期。雖然目前沒有其他介於其年代之間的化石紀錄,但亦可推知企鵝快速地發展出了龐大的軀體和優異游泳能力,並且占據了海中主要掠食者的位置,這樣的進展和陸地上的鳥類情況也頗為相似。而且 Kumimanu 和後面始新世巨型企鵝的年代之間,還隔著一群體型比較小的物種,這代表企鵝體型巨大化的發展出現了可能不只一次。
至於企鵝為何後來沒有持續發展龐大的體型?由於哺乳類重新回到水中,演化成鯨豚的年代正好吻合,有可能是鯨豚取而代之,不過這也只是相當間接的猜想,詳細的經過目前還不明確。
參考資料
- Ancient penguins may have weighed more than 100 kilograms, been as tall as a human. Science
- A Paleocene penguin from New Zealand substantiates multiple origins of gigantism in fossil Sphenisciformes.Nature Communications 8, Article number: 1927 (2017) doi:10.1038/s41467-017-01959-6