才到中正紀念堂站嗎?今天看書效率還挺高的。
孝和放下手中的講義。
Photo credit: George Alexander Ishida Newman 上大學後,他養成在捷運上閱讀的習慣。早上11點的捷運車廂空蕩蕩,彷彿是為了將郊區的新鮮空氣運送到市中而行駛,只有孝和與另一位乘客,那人身旁擺了個紙箱,乍看之下也是剛上大學的年紀,卻散發出一股同學沒有的氣息。正確地說,是少了大學生的青春氣息,更像社會人士。
為什麼可以這時候在捷運上,業務員嗎?不,業務員不應該穿Uniqulo襯衫跟牛仔褲……, 孝和猜測起對方背景,藉此打發時間。
列車抵達台電大樓終點站。孝和下車,轉身面對月台,等往公館的下一班列車。忽然,他意識到月台上只有自己一人。
那傢伙不見了。
※
幾天後孝和又遇見他了。
那人坐在相同的位子,偶爾看手機,大多時間往漆黑的窗外看著。或許是錯覺,孝和覺得投影在窗戶上的那張臉不時窺視自己。比起無趣的學校,曾經莫名其妙消失的傢伙讓孝和更感興趣。他沒在公館下車,一路來到了終點站新店。下車後,孝和保持一段距離,用眼角餘光觀察對方,兩人一前一後上電扶梯、出站。站外的洗手間,清潔人員正擺上「清理中」的黃色告示,那傢伙卻視若無睹地進去。
「不好意思。」
孝和低聲道歉後也跟了進去。
那傢伙站在最內側的小便斗前,與孝和對望了一秒,又像沒看見他似地,轉過頭吹起口哨。孝和走向小便斗。忽然,三間廁所門都被推開,三個邋塌的中年男子走出來,擋住孝和的去路,從他們緊靠的身上傳來一股刺鼻體味。孝和察覺不對勁,準備轉身離開,卻被一支拖把從背後頂住。
「不要動。」
清掃人員的聲音從看不見的死角傳來。
「上完廁所的瞬間最舒服了,呼。你是怎麼發現的?」
孝和沒回答。對方吹著口哨走過來,似乎是英國搖滾天團U2的「With or without you 」旋律。他伸出手:「我叫賴皮,你好。」
「你還沒洗手。」
※
Photo credit: arianne 「真的有『捷運地下委員會』這個組織?」
「敝人為初代會長,鏡頭在哪裡?」
「沒那種東西。」
孝和伸手制止賴皮比Ya的手勢。儘管剛認識,兩人卻像老友一樣打鬧著。孝和覺得賴皮和他高中死黨很像,都是思考很超展開的人。以前死黨還說過「籃球隊先發五人,棒球隊先發九人,為什麼女朋友只能先發一人」這種莫名其妙的話。
「不能拍照噢,禁止攝影。」
賴皮露出正經的表情,孝和吐槽道:「這裡是博物館嗎?」
事實上,這裡恐怕是跟博物館相差最遠的地方了。
在孝和眼前展開的是一條昏暗的捷運隧道,約四、五米挑高,往隧道深處望去有種整個人要被吸進去的錯覺。軌道上鋪了一好幾大片塑膠地板,他們坐在上方。空氣中瀰漫一股柴油發電的油氣味,幾十條電線從發電機出發,像地底才有的藤蔓品種,攀爬上水泥牆,抵擋不過重力,從隧道頂垂吊下來,開出一朵朵澄黃色的工業燈泡。不遠處,有一塊用伸縮圍欄拉出的區域,幾片模糊的身影側躺在那兒。更遠處有許多箱子,整齊堆疊著。
二十分鐘前,賴皮帶孝和搭上終點站是台電大樓的列車,
「趕快躲到椅子下。」,賴皮邊指揮孝和,自己躲到對面椅子底下。站務人員的腳從他們面前經過,沒停下來,不知道是沒看到,還是跟賴皮有默契。他們在折返的袋狀軌處扳開車門,步行到原本作為擺放備用列車,如今已荒廢的軌道。
這是捷運地圖上沒有的區域,同時也是捷運地下委員會的總部。
※
「還是不相信嗎?」
賴皮發出嘖嘖嘖的聲響,皺起眉頭:「人類真容易被『常識』束縛,常識裡不該有的存在,親眼見到了也無法相信。」
他裝起客服人員的腔調:「各位先生女士,捷運地下委員會起源於民國八十五年。當時淡水線剛通車,遊民喜歡躲進尚未啟用的隧道裡生活,當局發現後,一方面同情遊民生活,一方面怕強力驅趕引發社會問題,便睜一隻眼閉一隻眼。為了感謝捷運局通融,遊民主動幫忙工程。雙方就像小丑魚跟海葵互利共生。爾後捷運網路發達,遷徙至地下的遊民也越來越多,便成立了捷運地下委員會。除了協助工程,今年更將觸角延伸至送貨服務。」
「 送貨服務?」
賴皮點點頭:「捷運網路就像台北市的血管,血管能輸送氧氣,捷運當然也能送貨。」
我們不僅是小丑魚,還是紅血球。賴皮雙手插腰,一臉得意的樣子。
Photo credit: creativegaz ※
地下委員會的送貨方式是這樣的:某幾站的廁所掃具間裡設有販賣機,販售一張50元、上面繪製了「U2」的黑底紅字貼紙,販賣機上有QR code可加LINE ID。
「為什麼叫U2?」
孝和把玩著賴皮遞給他的貼紙
「因為是捷運(underground)的地下(underground)服務委員會啊,剛好兩個U。」
「台北捷運叫做MRT又不是underground,根本是因為你喜歡U2吧。」
「那是巧合。」
賴皮不理會孝和,繼續解釋:「客人得坐在第一節車廂末端的靠右三人座,將物品貼上貼紙,再用LINE告訴我們此刻正通過哪一站,要送達的車站,再把物品放在座位底下,我們就會去收貨。」
「不會被別人拿走嗎?」
賴皮用「這是什麼問題」的表情瞪了孝和一眼,「現在捷運上每個人都在玩手機,不會有人注意到座位底下的。況且,這裡是台北市,都市人最擅長對奇怪的事情裝作沒看到。」
果然又是常識害的嗎,孝和心想。
「收到後,我們會於24小時以內以遺失物品的名義送達到該站站務。之後,收件人就可以去取貨了。」
解釋完,賴皮又吹起口哨,這次換成U2的「Pride(In the name of love) 」。孝和採取正面攻擊發問:「幹嘛告訴我這麼多?」
「因為我們需要你的幫忙。」
賴皮露出狡猾的笑容。到這邊起才是重點。
※
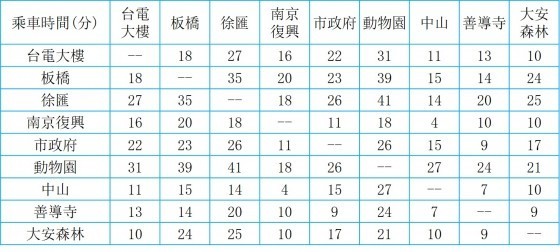
賴皮起身走向牆邊,孝和跟在後頭,牆上貼了幾十張表格,記錄捷運不同站間的乘車時間。
「我們最近送貨服務越做越好,開始有些忙不過來,所以得好好規劃起送貨流程。好比說,等等輪到仁叔送貨。」
賴皮往休息區一指,也不管孝和到底有沒有搞清楚仁叔是誰,
「他得送到『板橋、中山、動物園、徐匯中學、南京復興、市政府、善導寺、大安森林公園』八站。你覺得送貨順序怎麼排會比較好?」
「這是旅行業務員--」
Photo credit: katerha 賴皮打斷孝和,他說「我是這樣安排的:
賴皮的直覺法
台電大樓
板橋
徐匯
中山
南京復興
市政府
動物園
大安森林
善導寺
台電大樓
總和
18
35
14
4
11
26
21
9
13
—
151
根據捷運局公布的時間,需要花--」
「151分鐘。」
換孝和打斷賴皮。
「好厲害!這麼快就算出來了。」
賴皮提高音量,發出由衷的讚美,孝和的表情沒有任何變化,依然專注地看著牆上的表格。
「地表人真沒禮貌,被讚美了難道不該道謝嗎?」
「你有兩隻手跟兩隻腳,好厲害。」
「這跟那有什麼關係?」
「看吧,你也沒說謝謝。聽到對方陳述一件事實,本來就不需要道謝吧。」
賴皮做出下巴脫臼的誇張姿勢,然後嘴角露出反擊的笑容
「也是,畢竟是數學天才孝和嘛。」
突然被叫出本名,孝和還沒反應過來,一本書先出現在眼前,
「上週有人用我們的服務送了這本《超展開數學教室 》,我一看,就覺得書裡的人好眼熟,跟捷運上常看到的某位大學生很像。」
被將軍了,孝和哭笑不得。前陣子,他們高中時期和老師雲方用數學解決各種生活問題的經歷被出版後,死黨阿叉還用LINE問他:「怎麼辦,會不會有人在路上認出我們啊?」
「你放心吧,書被分在數學類科普,通常不會賣很好。」
「什麼嘛--」
孝和這才意識到原來阿叉是巴不得被認出來。沒想到先一步被發現的是他,還因為這本書被捲入了這近似都市傳奇的組織。
「我知道了。你要我幫忙排送貨流程嗎?」
賴皮點點頭,「跟聰明人講話真輕鬆。現在都靠我慢慢排,其他人懶得要命,要是不事先排好,他們就會隨便選。像仁叔每次都選『最近的下一站』,照他的方法這趟得花181分鐘,
最鄰近搜尋法
台電大樓
中山
南京復興
善導寺
大安森林
市政府
板橋
徐匯
動物園
台電大樓
總和
11
4
10
9
17
23
35
41
31
—
181
比我規劃的多了半小時,太浪費……」
賴皮劈哩啪啦講著,孝和將他的話視為背景噪音,腦海裡開始運算。等賴皮告一段落,他才開口
「這是標準的旅行業務員問題(Traveling salesman problem)。」
「嘎?」
「我剛一開始就說了,是你打斷我的。」
※
「想像有位業務員要造訪很多城市,城市間有道路連接。以造訪完所有城市為前題,業務員該如何規劃造訪順序,才能走最短距離、花費最少時間。」
孝和在地下幾十公尺深的地方上起數學課:「仁叔的『最近站為下一站 』是最鄰近搜尋法(nearest neighbor search)。」
「仁叔的方法也是數學家提出來的?當數學家也沒想像中的難嘛。」
賴皮不以為然說,孝和瞪了他一眼:「最鄰近搜尋法的優點在於簡單,但效果通常不好,用像你這種程度的大腦去規劃一下,往往就可以得到更好的結果。」
「太失禮了吧,什麼叫做『像我這種程度的大腦』,全台灣有誰比我更了解捷運,你能背出淡水信義線沿線每一站嗎?淡水、紅樹林……」
賴皮念咒似地背起來,孝和研究乘車時間表格,圈起其中幾個欄位。
「大安森林公園、信義安和、大安……顛倒了……這幾站安來安去真煩,你知道嗎,我常因此被下錯站的觀光客問路……101、象山站!」
「不錯嘛,真的背完了。」
「當然,哈哈。你把這幾個圈起來做什麼?」
孝和原本想說「這才叫讚美,因為你做了超乎預期的事」,但看到賴皮一臉得意,他反而失去了嘲諷的興致。
「另一種簡單的方法叫做貪婪演算法:每次都將最短的兩站間路徑加進路線。 比方說,中山站到南京復興之間的路徑最短,只要4分鐘,所以是第一條要納入的路徑。再來,善導寺跟中山站之間的路徑第二短,只有7分鐘,也要納入路徑。這麼一來會得到『善導寺→中山→南京復興』或反過來『南京復興→中山→善導寺』兩種路線。」
「再來是9分鐘的市政府到善導寺,路線擴充成『大安森林公園→善導寺→中山→南京復興』嗎?」
孝和點點頭。其實旅行業務員問題還有很多效果更好的演算法,例如插入法(insertion algorithm)、分支界定法(branch and bound),但講解起來太過複雜,他便選了跟最鄰近搜尋概念相似的貪婪演算法。孝和列出貪婪演算法結果:
貪婪演算法
台電
板橋
徐匯
大安森林
動物園
市政府
善導寺
中山
南京復興
台電大樓
總和
18
27
25
21
26
9
7
4
16
—
153
「共計153分鐘。」
「比我的規劃慢2分鐘。」
賴皮摸摸下巴,對孝和投以懷疑的眼神。孝和不屑地鼻子噴了口氣,冷笑說:「有經驗的人靠直覺解旅行業務員問題,本來就可以得到不錯的結果。但你剛才不是嫌只有你才會排嗎?貪婪演算法的話只要遵守規則,仁叔也能排出跟你精心設計路徑差不多的結果噢。」
孝和頓了頓,「只要善用數學,一般人跟『專家』的距離就能縮小。更何況我還沒講完。」
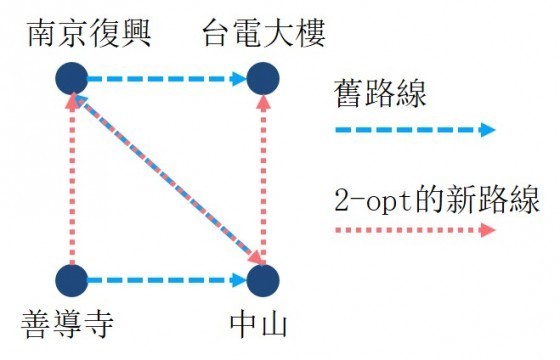
孝和指著倒數的中山站和南京復興說,「我們交換這兩站順序。從『善導寺→中山→南京復興 →台電大樓』變成『善導寺→南京復興→中山 →台電大樓』。有兩條路徑會因此變更。」
孝和畫出示意圖
「因為有兩條路變換,稱之為二元素優化(2-opt),優化後變成151分鐘,跟你的方法一樣了。」
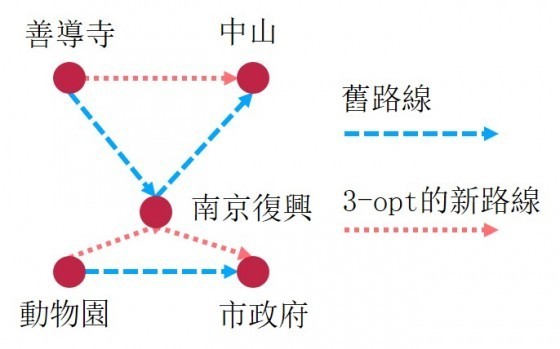
賴皮表情變得複雜,他既不想被超過,又因為找到好方法而開心。孝和看了好笑,用帶點安慰的口吻說:「你的路徑也可以靠2-opt改善。另一種方法是直接調整某站在排序裡的位置。比方說把南京復興從善導寺跟中山之間,移到動物園跟市政府之間。這個調整會導致三條路徑要重算,因此稱為『三元素優化(3-opt)』。」
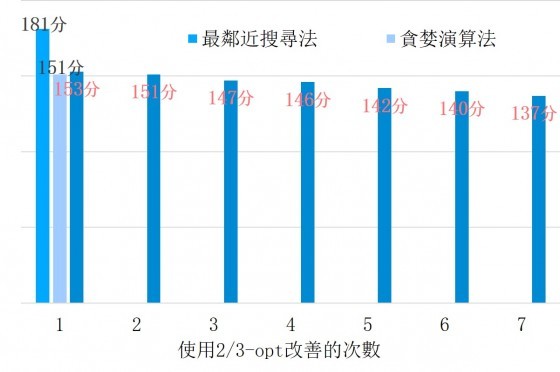
「優化後再少4分鐘。重複2/3-opt四次後可以得到這樣的結果
貪婪演算法+2/3-opt
台電大樓
板橋
善導寺
市政府
動物園
南京復興
徐匯
中山
大安森林
台電大樓
總和
18
14
9
26
18
18
14
10
10
—
137
只要137分鐘就能送貨完畢,比仁叔的方法快了25%。整套調整的方法稱為Lin-Kernighan演算法。」
賴皮拿起筆自己算起來,孝和注意到他握筆姿勢怪怪的,宛如小學生的字體逐漸填滿整張白紙。
幾十分鐘後,賴皮讚嘆:「原來這就是數學,將事情變得有邏輯,用有系統的方法解決。」
一個念頭在孝和心中閃過:「賴皮,你該不會--」
「嗯,我是在捷運上被發現的棄嬰。當時收留我的就是仁叔。捷運地下委員會最初也是為了照顧我而成立的組織。」
原來眼前的人連身分證都沒有,是真正的幽靈人口。
孝和揣摩著遊民們撿到賴皮時的心境。一個新生兒的出現,對他們來說必然是個負擔,但或許也帶來了生存下去最必須擁有的兩種情感:「希望」與「被需要」。
賴皮搔搔頭說:「名字是仁叔亂取的,我才不是真的姓賴咧。我的知識都是自學來的,雖然常聽說上學很無聊,不過我還是羨慕能上學的人。所以看到你們的《超展開數學教室 》才這麼興奮。我想體驗看看,就算一次也好,進教室聽課。」
「你會失望的。」
「失望也是人生的一部分。」
賴皮攤了攤手。孝和搖頭回答:「好吧。那你有沒有想過乾脆離開地底,回到正常社會生活呢?」
賴皮笑著回答:「對我來說這裡是家。儘管家裡比較髒亂,環境比較不好,但你會因此離開家裡嗎?」
孝和完全懂賴皮的意思。他自己也是這樣想,所以儘管這幾年來台灣狀況越來越不好,但他依然沒接受長輩們的建議,到國外念大學。一股莫名其妙的認同感驅使他說出:「好人做到底,我回去後寫個程式。以後你們只要輸入站名,程式就能輸出最佳送貨順序。」
「太棒了!身為地下委員會主席,我要好好感謝你的幫助。」
賴皮從口袋裡掏出厚厚一疊的貼紙。
「我授予你地下委員會榮譽委員,可終生免費使用送貨服務。」
誰需要這種東西啊,孝和正想推辭時:「附帶一提,你也可以在雨傘上貼這個。要是雨傘掉在捷運上,趕快傳LINE給我,我們立刻幫你送回去。這算是變形的失物代拾服務。」
這就蠻有用了,孝和收下了貼紙。賴皮轉身,俐落地從軌道跳上月台,回頭對賴皮伸出手:「我送你回去吧。」
遲疑了一下,孝和伸手與賴皮相握:「你到現在還是沒洗手。」
「哈哈哈。」
「賴皮這名字取得不錯,跟你的個性很貼切。」
「當然,家人取的嘛。」
孝和仰望月台上的賴皮,工業燈泡的光澤在他眼底流動,襯著昏暗的捷運地下隧道,顯得格外閃亮。
※
一周後,孝和把程式寄給賴皮,附了一份程式碼說明。如今每當想起有一群人,定居在巨大的捷運地下網路中,孝和就感到奇妙。
Photo credit: Y’amal 捷運車門打開,上午十一點的捷運空蕩蕩,彷彿只是為了運送郊區的空氣到市區。他從包包裡拿出一件籃球球衣,一本在二手書店找到的歷史小說,這是要給高中死黨阿叉以及他女友商商的。他在書裡夾了張紙條,上面寫了「下周四一起回學校看老師」,再將書與球衣裝進袋子,貼上U2貼紙。
捷運停車,上來一整群校外教學的國小學生,用高分貝的交談塞滿整節車廂。孝和站起來,往第一節車廂走去。來到最末端的座位,他瞥見座位底下隱約有個物體的輪廓。有人先一步送了貨嗎?他彎下腰檢查。
此時,後方傳來一陣熟悉的聲音:「客人,送貨嗎?」
註:更多孝和的故事,請參考《超展開數學教室 》
Photo credit: Stacy