台大和中研院最近聯手解開了古菌感光蛋白結構上的秘密。當我想跟認識的朋友說明這個研究的內容時,卻發現好多需要的知識背景,都不在高中所學的生物背景裡。看來值得特別寫段文字,來幫助不是這個領域的人瞭解這個有趣的研究主題。
古菌,是古代的細菌嗎?
要介紹這種特殊的菌種,得要先從古菌講起。這星球上的生物由一個個細胞構成,有生物構造簡單,全身上下就是一個細胞而已,歸類為單細胞生物。我們則是由很多細胞組成的多細胞生物。如果你仔細看看單細胞生物每個細胞的構造,又可以根據這細胞有沒有細胞核來做區分。有的單細胞生物的細胞比較小,細胞裡面沒有細胞核。這種生物被歸類為原核生物,是種比較簡單的生物。有的細胞比較大,細胞裡有個細胞核,把 DNA 好好地收在裡面。這種生物被歸類為真核生物,代表"有細胞核"的生物。人類的細胞有細胞核,所以分類上我們是多細胞的真核生物。
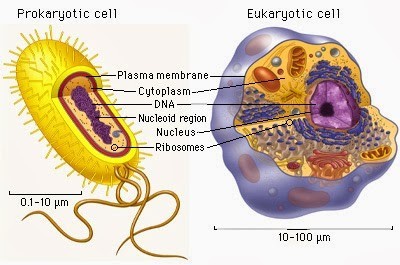
原核生物又可以再被區分成兩大類,是生物在演化時出現的兩大分支。一個分支叫做細菌(Bacteria),一個分支叫做古菌(Archaea)。這兩大分支在地球生物演化史上互相競爭,細菌搶到了地球,現在遍佈各地。而古菌因為競爭能力輸人,所以現在你大致只能在比較奇怪的環境下找到它們,例如在極酸、極熱、極鹹的地方,通常會是古菌的天下。而在古早的某個年代,有隻古菌把細菌納入自己的細胞裡開始了共生關係,而這樣新組成的細胞後來變成了最早的真核細胞,很久以後才演化出我們這些動物。所以如果真的要坳,某種程度來說,我們也算是古菌的後代子孫。
窩氏鹽方扁平古菌是什麼奇怪的生物?
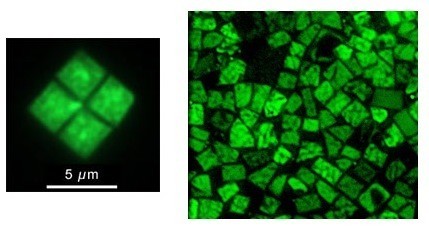
1980 年 A. E. Walsby 在埃及鹽池裡分離到一種奇怪的古菌,並將它命名為窩氏鹽方扁平古菌(Haloquadratum walsbyi)。為什麼說它奇怪呢?細菌或古菌的細胞通常是圓形(球菌),拉長一點變嘟嘟好香腸形(桿菌),再拉長一點變成熱狗形(長桿菌)。可是鹽方扁平古菌是正方形的,一隻隻排得整整齊齊,像地上貼的小方塊磁磚。這種古菌普遍出現在全球各地的高鹽環境裡,像是鹽田裡讓鹽結晶析出的結晶池裡。一般生物在這種環境馬上會因為高鹽而脫水,於是鹽方扁平古菌沒有敵手,輕鬆成為這種環境裡的優勢物種。
不過要生活在這樣的環境裡是很辛苦的。由於其它生物都活不了,這種環境裡也不會有多少養份可以利用。這些古菌有個讓自己存下來的秘密武器,叫做菌視紫質(bacteriorhodopsin)。會叫做菌視紫質,是因為它跟人類眼睛裡感光用視紫質(rhodopsin)的結構類似而得到這個名字的。菌視紫質可以在有光的時候利用光能把氫離子輸送到細胞膜外,形成氫離子濃度差。而古菌可以再利用這個濃度差來合成細胞需要的能量分子 ATP。也就是說,有了這個蛋白質配備,這隻古菌只要照光就可以產生自己需要的能量,就像裝了光電板一樣。這在一來,即使環境中沒有太多養份可以利用,古菌一樣可以過著安穩的生活。目前已經在多種古菌上發現這種能讓古菌靠太陽吃飯的配備,是個很好用的工具。
窩氏鹽方扁平古菌的菌視紫質
2015 年 12 月,台大生化科技系楊啓伸副教授與中研院王惠鈞副院長的實驗室合作發表了一篇關於窩氏鹽方扁平古菌的菌視紫質特殊結構的論文,發表在頗富盛名的期刊 Journal of Biological Chemistry 上。因為菌視紫質會把細胞質裡的氫離子送到膜的另一端,所以必須是個放在細胞膜上的蛋白質。在研究蛋白質結構時需要利用結晶技術,先大量純化出這種蛋白質,接著讓蛋白質結晶,有了晶體後才能研究它的結構。不過如果我們想知道膜蛋白和膜結合時就麻煩了,因為有膜和蛋白質放一起,就很難產生結晶。這個研究團隊能得到夠多蛋白並成功解出結構,實在是很厲害。由於我沒有蛋白質結構分析方面的專長,結構上的有趣之處還請真正的專家來做說明。
在微生物生態上,這篇研究提供了一個非常有趣的答案。過去被研究過的菌視紫質如果被放在酸性環境下,會接上氫離子,讓菌視紫質不能和視黃醇(retinol)結合,而失去原本幫浦的功能。而這篇研究發現窩氏鹽方扁平古菌的菌視紫質,在結構上可以不讓氫離子進來卡位,於是在酸性環境還可以持續運作。對這細菌來說好處是,如果環境真的變得越來越酸,其它同樣利用光能的古菌可能被迫停止利用光能。但是窩氏鹽方扁平古菌因為有著這個在設計上有小改變的裝備,還是可以繼續輸送氫離子而得到能量。