在「巨人」附近駕駛太空船是一件難事,因為航行速度必須非常快。
行星、恆星或太空船要想在這裡存續下來,就必須以同等強大的離心力來抗衡「巨人」的強大重力。這表示它必須以非常高速移動。
事實證明它必須達到近光速才行。在我對《星際效應》相關科學的詮釋中,「永續號」派遣隊員登上米勒的星球時,它是停駐在「巨人」半徑五倍的距離之外,繞行速率為光速的三分之一:c/3(c 代表光速);米勒的行星則以55% 光速運行,即0.55c。
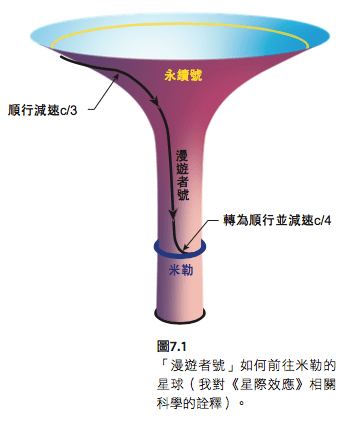
在我的詮釋中(圖7.1),「漫遊者號」要從停駐軌道抵達米勒的星球,必須先減慢它的順行運動,從c/3 降至遠低於此,然後「巨人」的重力才能夠拉它向下。等來到星球附近時,「漫遊者號」又必須從下行轉為順行。而由於下墜時的加速,這時它的航速已經高出太多,因此必須減速c/4(四分之一光速),降低到該星球的速度0.55c,才能前往米勒的星球。「漫遊者號」的駕駛庫柏可能使用哪種機制來執行這種劇烈的速度變化?
二十一世紀的技術
他必須達成的速度變化約為c/3,相當於每秒十萬公里。(這不是時速,是秒速!)相形之下,今天我們人類推力最強的火箭,秒速可達十五公里,約十萬公里的七千分之一,實在太慢了。
《星際效應》片中的「永續號」從地球航向土星花了兩年時間,平均速度為每秒二十公里,是十萬公里的五千分之一,一樣很慢。人類的航空器在二十一世紀有可能達到的最高速度,我認為是每秒三百公里,而這得先大量投入核能火箭研發作業才能辦到,但這仍只是《星際效應》所需速度的三百分之一左右,還是太慢。
所幸,大自然提供了一種做法來落實《星際效應》片中必須達成的龐大速度變化(c/3):運用重力彈弓效應繞過遠比「巨人」小上許多的黑洞來助推加速。
彈弓助推航向米勒的星球
像「巨人」這麼龐大的黑洞,周遭會聚集許多恆星和小型黑洞(下一節就會深入討論)。
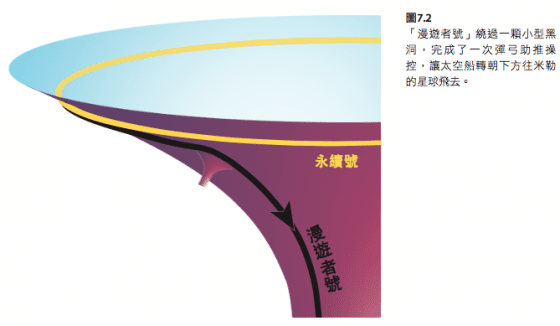
在我的《星際效應》相關科學詮釋中,我設想:庫柏和他的團隊調查了所有繞行「巨人」的小型黑洞,確定其中有一顆黑洞的所在位置可供「漫遊者號」進行重力轉向作業,推動它從近圓形的軌道,轉向往米勒的星球俯衝而去(圖7.2)。
這種重力助推操控的方法,稱為「重力彈弓效應」(gravitational slingshot),美國航太總署也經常在太陽系內善加運用,但是是借助行星的重力,而非黑洞(見本章末尾)。《星際效應》片中沒有呈現或談到這種助推操控法,只讓庫柏說出下面這段話:「聽著,我可以繞過那顆中子星來減速。」
減速是必要的動作,因為「漫遊者號」受到「巨人」重力的龐大引力而下墜─從「永續號」的軌道降到米勒星球的軌道─它的速度已經拉得太高,行進速度比米勒的星球高出c/4。
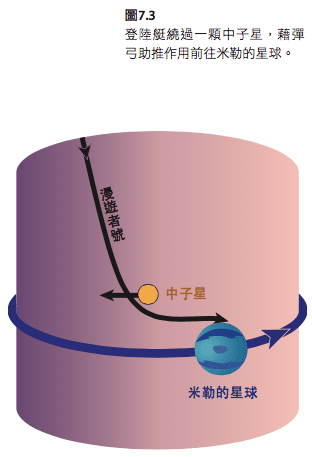
圖7.3 所示的中子星,相對於米勒的星球朝左行進,「漫遊者號」就靠它來轉向、減速,然後才能正常接近那顆星球。
這種彈弓效應有一種特點可能會讓人非常不快,甚至會奪走人的性命,那就是:潮汐力(第四章)。速度變化要達到c/3 或c/4 的幅度,「漫遊者號」必須充分靠近小型黑洞和中子星,才能受到它們強大重力的影響。
在這麼近的距離下, 倘若那顆偏轉天體(deflector)是中子星,或是半徑不到一萬公里的黑洞,則「漫遊者號」和上頭的人類都會被潮汐力撕碎(第四章)。
「漫遊者號」和人類要想存活,這個偏轉天體就必須是至少一萬公里大的黑洞(大小約如地球)。大自然中確實存在這種大小的黑洞,統稱為中等質量黑洞(intermediate-mass black holes, iMBh),這尺寸其實已經很大,但和「巨人」比起來仍顯渺小:只有它的萬分之一。
本來克里斯多福.諾蘭應該用一顆地球大小的中等質量黑洞來幫「漫遊者號」減速,結果他用了一顆中子星。他一開始改寫喬納森的電影劇本時,我就和他討論過這件事。討論過後,他仍然選定中子星。為什麼?因為他希望電影裡面只出現一個黑洞,才不會把廣大觀眾搞糊塗了。一個黑洞,一個蟲洞,還有一顆中子星,加上片中其他的豐富科學素材,全都要在兩小時的快節奏影片中讓觀眾吸收。
克里斯多福認為,這些素材是他能處理的極限。既然在「巨人」附近航行必須借助強大的重力彈弓效應,於是克里斯多福將一次彈弓效應放進庫柏的對白,卻也付出了代價,用了不合乎科學原理的偏轉天體:以中子星取代了黑洞。
星系核內的中等質量黑洞
一顆一萬公里的中等質量黑洞,重約一萬顆太陽的質量,相當於「巨人」的萬分之一,但已經是普通黑洞的千倍重量了。這正是庫柏需要的偏轉天體。有些中等質量黑洞據信是在恆星密集的星團─稱為「球狀星團」(globular cluster)─的核心內形成的,當中又有一部份可能循徑進入有巨型黑洞棲身的星系核(Galactic nuclei)內。
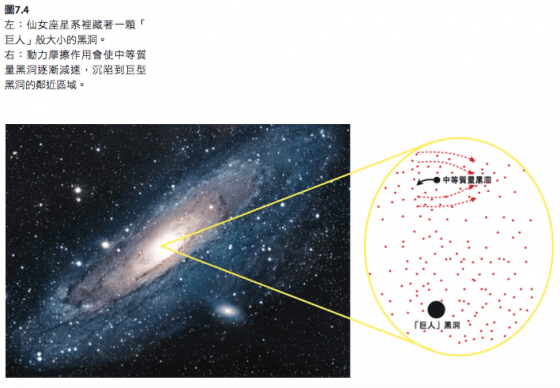
仙女座星系就是一個好例子。它是最接近我們銀河系的大型星系(圖7.4),星系核裡潛藏了一顆「巨人」尺寸的黑洞,擁有一億顆太陽的質量。數量龐大的恆星被拉進這種巨型黑洞的鄰近區域;每立方光年多達一千顆。
當一顆中等質量黑洞穿過這種密集區域,它發出的重力會讓恆星偏斜轉向,製造出一道更高密度的尾流,跟在它的身後(圖7.4)。這道尾流以重力拉動中等質量黑洞,使中等質量黑洞減速,這種過程就叫做「動力摩擦」(dynamical friction)。而當中等質量黑洞非常緩慢地減速時,它也漸沉漸深,進入巨型黑洞的鄰近區域。
在我為《星際效應》相關科學所做的詮釋中,大自然可以用這種方式為庫柏提供一顆中等質量黑洞,滿足他進行彈弓助推的需求。
思考與挑戰:超先進文明的軌道航行
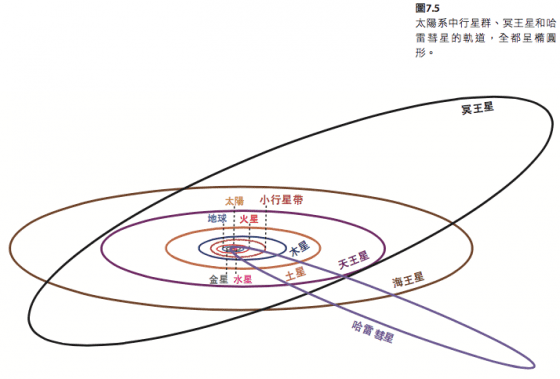
在太陽系中,行星和彗星的軌道全都呈非常準確的橢圓形(圖7.5)。牛頓的重力定律為此提出保證,並且堅持主張這一點。
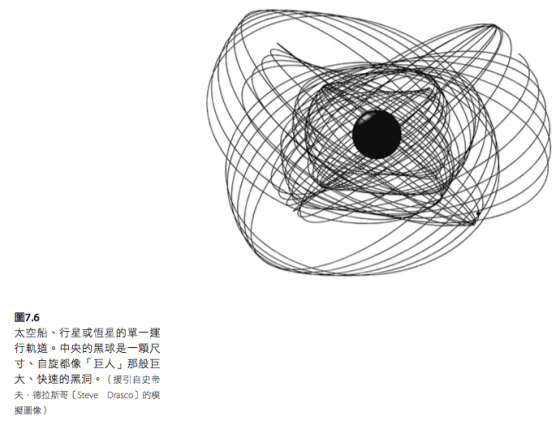
相對來說,一顆像「巨人」那樣快速自旋且體型巨大的黑洞周遭─這裡是愛因斯坦的相對論定律主宰之地─那些軌道就遠遠更加複雜了。圖7.6 就是一例,任意繞行「巨人」一圈,都需要好幾小時到好幾天,因此圖7.6 中畫出來的軌道大約需要一年時間才能走完;或許幾年之後,它的軌道就會經過幾乎所有你想去的目的地,只是你的速度有可能不符所需,或許會需要來一次彈弓助推來改變速度,才能達成會合的目標。
我就讓各位自行想像一下,超先進文明有可能怎麼利用這種複雜的軌道。在我對這部電影的科學詮釋中,我為了簡單起見,大致上會避開它們,把重點放在圓形的赤道軌道上(例如「永續號」的停駐軌道、「米勒的星球」繞行軌道,以及臨界軌道),以及「永續號」如何從一條圓形的赤道面軌道轉換到另一條之上。當中只有一個例外,那就是曼恩的星球,但這部份我們等第十九章再來討論。
美國航太總署的太陽系內重力彈弓助推
現在就讓我們從(物理定律所容許的)「可能性」世界,回到鐵面無情的現實中,看看截至二○一四年為止,人類在太陽系的舒適牢籠裡,實際完成了哪些重力彈弓作業。
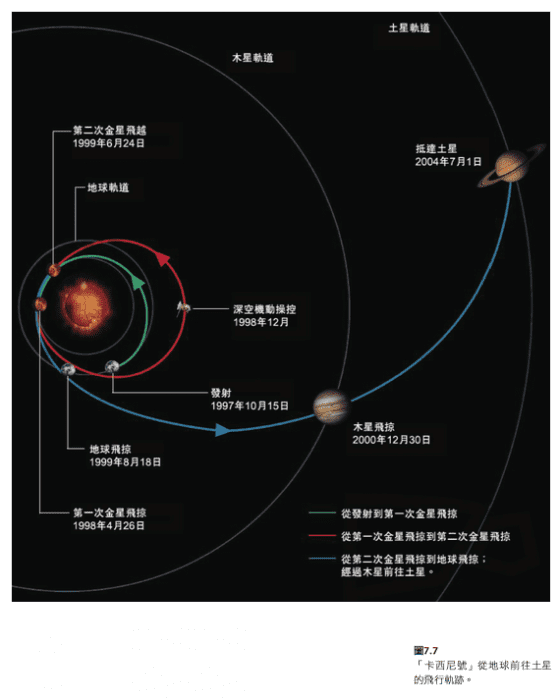
各位或許對航太總署的「卡西尼號」(cassini)太空船並不陌生(圖7.7)。「卡西尼號」在一九九七年十月十五日從地球發射升空,船上搭載的燃料並不足以讓它飛抵目的地土星。這不足的部份,就是運用幾次彈弓助推來解決:一九九八年四月二十六日繞過金星;一九九九年七月二十四日完成二度繞行金星的彈弓助推,接著在二○○○年十二月三十日繞過木星。二○○四年七月一日,「卡西尼號」終於抵達土星,之前還繞過最貼近土星的衛星「木衛一」(io),借助一次彈弓作業來降低航速。
這一系列的彈弓助推作業,沒有一次和我前面所描述的相同。前面我提到彈弓效應會強力偏轉太空船的行進方向,但金星、地球、木星和木衛一卻只讓太空船稍微轉向。為什麼?
因為偏轉天體的重力太弱,沒辦法強力偏轉航向。以金星、地球和木衛一來說,偏轉影響必然都很微弱,因為它們的重力原本就很弱。木星的重力雖然強大得多,但大幅偏轉會把「卡西尼號」送上錯誤航向,因此必須使用較小幅偏轉作業以抵達土星。
這幾次偏轉幅度雖然都很小,「卡西尼號」仍然從飛掠作業取得充裕的推力,足以彌補燃料的不足。每一次飛掠(木衛一那次除外),「卡西尼號」都是尾隨著偏轉行星前行,但角度得以讓行星的重力以最理想的方式拉著它向前行進並提增飛航速度。《星際效應》片中的「永續號」也曾繞行火星完成一次近似的彈弓作業。
「卡西尼號」在過去十年中探訪了土星和土星的衛星群,傳回了令人稱奇的影像和資訊─蘊涵著美感和科學的寶藏。各位可以上網一瞥端倪:http://www.nasa.gov/mission_P.s/cassini/main/
相對之下,「巨人」的助推就不像太陽系內的彈弓效應那麼弱小。它的重力非常強勁,就算是以超高速行進的物體,它也抓得住,然後還能以大幅偏折的彈弓效應,將它們拋向四面八方,連光線也不能倖免,從而造成重力透鏡效應,這個讓我們得以見到「巨人」身影的關鍵。