文/ Rinus Roelofs
譯/余筱嵐
「立面化」(elevation)
在《神聖比例》(La Divina Proportione)一書中,盧卡・帕西奧利(Luca Pacioli)及李奧納多・達文西(Leonardo Da Vinci)介紹了立面化的柏拉圖立體及部分立面化的阿基米德多面體。圖一及圖二正是達文西所繪製的柏拉圖立體及立面化的柏拉圖立體。
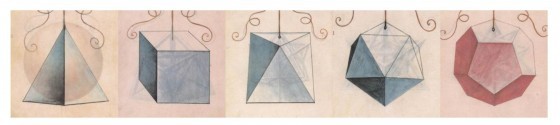

何謂多面體的立面化結構?在《神聖比例》第49章中第6及第7段,帕西奧利描述正6面體的立面化結構如下:“⋯⋯它被24個三角形的面包圍,這個多面體的外觀是由6個四角錐所構成,內含一個正6面體,這6個四角錐即分別放置在此正6面體的6個面上。然而,我們只能想像這個正6面體的存在,因為在外觀上,它被6個四角錐緊密包覆,而這6個正方形的面正是這6個四角錐的底面。”
總和而言,這個物體是由24個正三角形的面加上6個隱藏的正方形的面所構成,如圖三分解圖所示。
關於立面化的八面體(octahedron elevatus),帕西奧利寫道(第50章中第19及第20段):“這個物體的外觀是由8個三角錐所構成,內含一個正8面體。”表示這個物體是由32個正三角形的面所構成。當然,其中8個是隱藏的。

「星狀化」(stellation)
帕西奧利並沒有真的給「立面化」下一個定義,但是他的描述是非常明確的。在1619年,大約一個世紀後,克卜勒為多邊形及多面體定義「星狀化」:這是一個延伸邊或面的過程,直到這些延伸的邊或面相遇而產生新的多邊形或多面體。
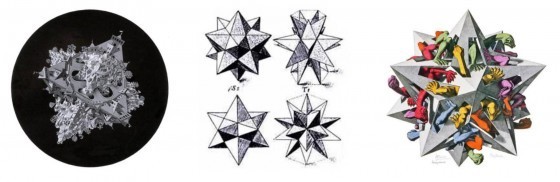
根據克卜勒的定義,星狀化的正8面體的面數和正8面體的面數一樣,因為正8面體中8個三角形的面延伸成為8個較大三角形的面,這些較大三角形的面兩兩相交成為星狀8面體(Stella Octangula),或者也稱為克卜勒星狀多面體(Kepler Star)。艾雪(M.C. Escher)的作品「兩個世界」(Two worlds,圖四)可以讓我們看見這個物體,事實上,正是由兩個互穿的正4面體組合而成。
「立面化」vs. 「星狀化」
立面化正8面體與星狀化正8面體有一個根本的差異,立面化正8面體有32個面,而星狀化正8面體則有相交的8個面。除此之外,還有一個重要的差異,在克卜勒的定義中談及了一個過程,但帕西奧利的描述則僅止於最終的結果,然而,我們可以重新定義立面化的過程為:多面體立面化的過程,是一個將多面體上每個面的中點向外提升,直到提升的中點與原來多面體的面相鄰的兩個頂點構成正三角形為止。
推廣這個定義,可以不必要求這些三角形必須是正三角形。根據這個定義,帕西奧利的立面化正12面體,可視為在正12面體與克卜勒星狀12面體之間的一個步驟。艾雪(M.C. Escher)作品「重力」挪去部分星狀結構的面,讓我們更清楚看見這個構造。關於這個作品,艾雪寫道:“在正12面體的每個面上,我們可以看到各有一隻怪獸,牠的身體被五角錐所捕獲。”這和帕西奧利描述的立面化多面體十分相似。採用立面化的新定義,我們可以比較由正12面體構成立面化正12面體的過程,以及由正12面體構成克卜勒星狀12面體的過程。
圖七及圖八顯示正12面體上半部(僅顯示正12面體其中6個五邊形的面)立面化及星狀化的過程,在立面化的過程中,第三個步驟顯示的物體即為《神聖比例》書中發表的物體。但是,當我們繼續這個立面化的過程,我們將得到與星狀12面體相似的結果。因為,此時立面化形成的三角形的面,與原來正12面體的面共面。兩個最終物體最大的不同在於面的個數,立面化正12面體仍然保有五邊形的面,所以,兩個物體都是雙層的結構。


二次星狀化
由正20面體三角形的面開始延伸產生星狀20面體,圖九顯示動態過程中的四個步驟,在星狀化的過程中,這是我們得到一個新的多面體,每個面的(第一個位置)單元構件。(圖十)


不過,我們可以繼續這個過程,並且進一步延伸這些面(圖十一),將得到(第二個位置)每個面的單元構件,所構成的多面體,如圖十二所示。


就像艾雪的作品「重力」,我除去了每個面的一部份,讓構造更顯而易見。我十分著迷於現在每個面上所呈現的結構,它並不是一個三角錐,而是三個某個程度變形的三角錐彼此相交的結構。所以,再一次星狀化過程的結果產生非常有趣的結構。現在引發的問題是:在立面化的操作中,也有可能產類似的情形嗎?我們可以定義二次立面化嗎?我們可以期待將會生成什麼樣的物體呢?
二次立面化
採用推廣的立面化定義並應用於正8面體,向外提升正8面體每個面的中點,直到所產生的新形體類似於另一個多面體為止。在這個操作下,第一個得到的是菱形12面體。在這個菱形12面體上,再次採用同樣的操作,並且稱其結果為正8面體的二次立面化,我們停止此操作於:所提升的面與原來菱形12面體的面共面。

最右邊的圖形與艾雪所建構的其中一個多面體一樣(圖十四),並且使用於其作品「瀑布」(Waterfall)中(圖十五)。

「立邊化」
進一步探討最終的圖形(圖十三),讓我得到一個結論,我們也可以將此圖形視為:在正8面體的每個邊上,都有一個某個程度變形的菱形角錐,而這十二個角錐圍繞此正8面體。意思是說,我們也可以提升正8面體每個邊的中點,得到一樣的圖形。因此,我們可以定義一種新的變換:「立邊化」(Edge Elevation)。立邊化的操作方式為:每個邊的中點與每個面的中點連接,接著提升每個邊的中點,伸展直至此連結(在原來每個邊的位置上)形成由周圍(不包括底面,底面為菱形)四個三角形構成的角錐為止。


圖十六描述的正是這個操作的過程。圖十七則顯示同樣的過程,但是採用艾雪在作品「重力」(圖六)中的手法,展示其結構。
正4面體及正20面體
當我們應用立邊化於其他多面體,比如說:正4面體及正20面體,這些物體發展的過程如圖十八及圖十九。立邊化正20面體最終的狀態與二次星狀化正20面體類似。至於正4面體經由立邊化的操作後,我們則得到一個新的物體。


構造元件
縱使立邊化正20面體看起來與二次星狀化正20面體類似,然而,其中卻有很大的不同點。當我們分析兩個物件的構造,我們會發現它們的面是不一樣的。圖二十的左邊是二次星狀化正20面體的一個面,而右邊是兩個相鄰的立邊化正20面體的面。為了建構立邊化的多面體,我用鐳射切出了這些面,兩個面一組,兩面共用的邊即為其上的摺線,紙的模型顯得相對容易建構。

我首先連接三組面,開始建構立面化正20面體。

如同各位所見,當我們連接越多元件,外部的結構變得十分複雜,然而,多面體的內部結構則一直是菱形的圖案。(圖二十二及圖二十三)

例子:測地線球面(Geodesic Sphere)
提升多面體邊的中點之操作方式,可應用於更多不同的物體。比如說:我限定自己嘗試三角形所構成的物體,這些三角形並不需要是正三角形,如圖二十四至圖二十七的測地線球面。因為這些構造都是雙層的,所以十分堅固,甚至可以建構穹頂構造。


例子:柱面(Cylinders)
最後一個例子,我想呈現柱面的構造。(圖二十八及圖二十九)其根本的多面體是螺旋狀的三角化多面體(helical deltahedra)。我想我們可以總結:「立邊化」是一個有趣的新操作,讓我們可以產生出許多有趣的構造。

參考資料:
- Peter R. Cromwell, Polyhedra, Cambridge University Press, UK, 1997.
- Luca Pacioli – Leonardo da Vinci, La Divina Proportione, 1509, Ed. Akal, S.A., Madrid, 1991
- Luca Pacioli, Divina Proportione: Die Lehre Vom Goldenen Schnitt, 1509, Ed. Carl Graeser, Wien, 1896.
- Red. J.W. Vermeulen, Hetoneindige, M.C. Escher over eigen werk, Meulenhoff, Amsterdam, 1986.
- Magnus J. Wenninger, Polyhedron Models, Cambridge University Press, UK, 1971.