混沌使我們了解,遵循簡單規則的系統可以表現出驚人的複雜行為,這對每個人都是很重要的教訓,包括那些以為嚴謹管束的公司就能自動平穩營運的經理階層;自以為針對問題立法,便能消滅問題的政治人物;以為替某個系統找出模型,就等於完工的科學家。
但這個世界也不可能完全混沌一片,否則我們根本無法生存。事實上,混沌現象遲至今日才被發現的原因之一,就是我們這個世界在許多方面仍舊相當單純。當我們向深層探索時,這種單純性通常就會消失,可是在事物的表面它依然存在。
我們用來描述這個世界的語言,即奠基在這些單純性之上。例如,「狐狸追逐兔子」這個敘述之所以有意義,只是因為它掌握了動物互動的一般模式。狐狸的確會追逐兔子,這也就是說,當一隻餓狐狸看到兔子時,牠就很有可能窮追不捨。
看似簡單,實則複雜
然而,我們若是開始注意細節,單純性很快就會消失,一切都會變得複雜無比。比如說,為了進行「窮追不捨」這簡單的行動,狐狸必須先能認出兔子,然後還得做好拔腿飛奔的準備。想要了解這些行動,我們必須先了解視覺、模式辨識(pattern recognition)與運動。

在第七章中,我們探討了第三點:運動,發現它牽涉到生理學與神經學的複雜現象,包括骨骼、肌肉、神經與腦部。而肌肉的行動又由細胞生物學與化學決定;化學則由量子力學主宰;至於量子力學,又可能受制於千呼萬喚始出來的萬有理論(Theory of Everything)。在萬有理論之中,所有的物理定律都統一於整體架構之下。
如果我們暫且忽略運動,改為研究視覺或模式辨識所開拓的領域,我們仍將發現同樣不斷開枝散葉的複雜性。
由於只有我們的出發點具有單純性,所以,若非大自然的確利用了複雜無比的因果網絡,就是自然界的機制與大部分複雜性無關。看來,想要一探究竟似乎毫無希望。
直到最近為止,科學研究的自然途徑都是順著複雜性這棵大樹,不斷向下挖掘。這就是寇恩與我所謂的「化約論者(reductionist)的噩夢」。沿著這條傳統路徑,我們學到很多關於大自然的知識,尤其是如何操控大自然為我們服務的知識。
但是我們再也無法見到巨大的單純性,因為我們不能再將它們視為單純的現象。
近年來,有人提出一個根本不同的途徑,統稱為「複雜理論」(complexity theory)。它的中心課題,是眾多成分之間的複雜交互作用所產生的大尺度單純性。
在本書這最後一章,我準備介紹三個複雜性產生單純性的例子。它們並非取材自複雜理論學家的著作,而是我從當代應用數學的主流「動力系統理論」所選出來的。
我這樣做有兩個原因:一來是想證明複雜理論的中心思想已出現在所有科學中,與任何刻意提倡它的行動無關;一場寧靜革命已經接近沸點,其實我們都能看得出來,因為不少氣泡都開始冒出了水面。
另一個原因是,它們各自解決了自然界數學模式的一個歷史大謎,讓我們因此眼界大開;如果不是藉著這些問題,我們根本無法體會自然界的這些特色。這三個題目分別是:液滴的形狀、動物群體的動態行為,以及花瓣數目的奇異數字模式(我在第一章曾提到會在這裡揭曉謎底)。
你真的知道水滴的形狀嗎?
首先,讓我們再回到水滴從水龍頭緩緩滴下的問題。
這是個天天可見的簡單現象,但它已為我們提供了混沌的知識。現在,我們還要藉它來了解複雜性的一些面貌。這一回,我們注意的焦點不再是水滴的時間間隔,而是準備研究當水滴脫離水龍頭時,它的形狀究竟是什麼樣子。
這難道不是很明顯嗎? 它一定是個眾所周知的「淚珠」狀,有點像隻蝌蚪,前頭是圓形,漸漸彎成尖尖的尾巴。畢竟淚珠就是這種形狀。但它並不明顯,事實上,它根本不正確。
當我首次聽到這問題的時候,我主要的驚訝來自這個答案並沒有太長的歷史。有關流體的科學研究簡直汗牛充棟,說它們占據圖書館中數英里的書架絕不誇張,當然其中應該已有人費心觀察過水滴的形狀。
然而,早期文獻中只有一張圖畫正確,那是在超過一個世紀之前,由物理學家瑞利男爵 (John William Strutt,Lord Rayleigh, 1842-1919)所繪製的。由於那張圖畫太小了,所以幾乎沒有人注意到。一九九○年,英國布里斯陀大學(Bristol University)的數學家佩里格萊恩(Howell Peregrine)等人將這個過程拍攝下來,發現它比任何人想像中的還要複雜得多,但是也有趣得多。

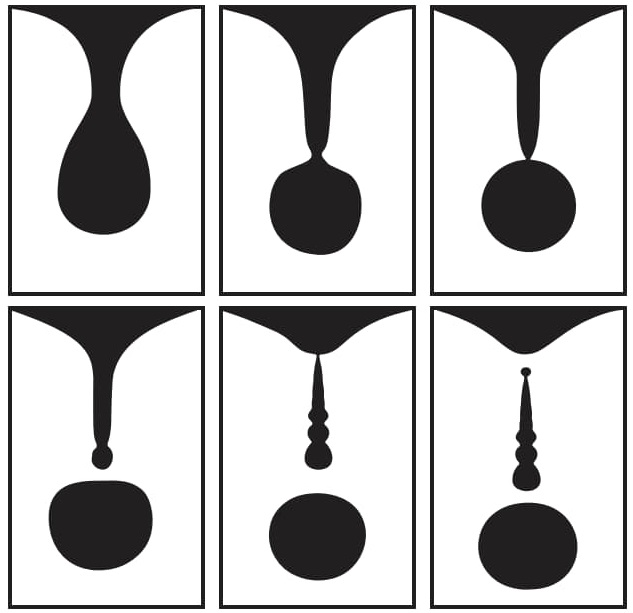
一滴水滴形成之初,是懸掛在水龍頭尾端水面的一個鼓脹部分。它會慢慢形成一個腰身,這個腰身愈變愈細,下端的水滴則漸趨傳統的淚珠狀。在一般人的想像中,這個腰身會被掐斷,形成一個又短又尖的尾巴。可是事實上,腰身卻會愈拉愈長,變成一根細長的圓柱,下端則懸掛著一個幾乎接近球形的水滴。
接下來,圓柱與球形接觸的部位開始變得更細,最後成為一個尖點。在這個階段中,整體的形狀看來像是一支毛線針按在一個橘子上。「橘子」隨後便從針尖處脫離,然後它一面墜落,一面還在進行輕微的脈動。
不過故事並沒有結束。現在,毛線針尖銳的尾部開始變圓,還會有微小的波動向上傳到它的頂端,使它看起來好像一串愈上面愈小的珍珠。最後,這根圓柱的頂端收縮成一個尖點,然後整根圓柱也掉了下來。在墜落的過程中,它的頂端變成了球形,並有了一系列複雜的波動沿著它上下傳遞。
我希望各位讀者也像我一樣感到驚奇,我從沒有想到墜落的水滴會這麼「忙碌」。
這些觀察解釋了為何過去沒有人研究這問題的數學細節,因為它實在太過複雜了。當水滴脫離時,系統會產生一個奇異點(singularity),該處的數學將變得十分棘手。毛線針的針尖就是這個系統的奇異點。可是為什麼會有一個奇異點呢?為什麼水滴要以這麼複雜的方式脫離呢?
一九九四年,艾格斯(J. Eggers)與杜邦(T. F. Dupont)證明這是流體力學方程式的必然結果。他們利用電腦模擬這些方程式的演化,在電腦中重現了佩里格萊恩發現的情節。
-scaled.jpg)
——本文摘自《大自然的數學遊戲 》,2022 年 11 月,天下文化出版,未經同意請勿轉載。





































《運動基因》立體封面72dpi.jpg)