- 作者:洪秉驊、張皓崴、陳澔龍/國立新竹科學園區實驗高級中等學校
「數感盃青少年寫作競賽」提供國中、高中職學生在培養數學素養後,一個絕佳的發揮舞台。本競賽鼓勵學生跨領域學習,運用數學知識,培養及展現邏輯思考與文字撰寫的能力,盼提升臺灣青少年科普寫作的風氣以及對數學的興趣。
本文為 2021 數感盃青少年寫作競賽 / 高中組專題報導類佳作之作品,為盡量完整呈現學生之作品樣貌,本文除首圖及標點符號、錯字之外並未進行其他大幅度編修。
壹、前言
網際網路是現代生活不可缺少的一部分,人們都依賴網路來完成生活中的大小事。若不幸地沒有網路,在科技產品中,我們還能從何找到樂趣呢?相信許多人在網路斷線時, 都會手癢而打開谷歌裡的小恐龍遊戲吧!
這個經典的作品是由 google chrome 在 2014 年推出的,在 chrome 瀏覽器網路斷線情況下,點擊圖中的恐龍圖案,恐龍便會開始奔跑。

沙漠中,迎著飛奔的小恐龍而來的是仙人掌、翼手龍等阻礙,玩家便需要透過空白鍵(往上跳)、向下鍵(往下躲),帶著小恐龍在無邊無際的沙漠中奔馳。而若不慎碰到以上障礙物,使小恐龍受了傷,遊戲便會結束。
這個遊戲在早期行動網路缺乏的時代,成為了用戶最喜歡的遊戲之一。甚至,還有人以外掛程式賦予小恐龍辨別阻礙的智慧,讓牠得以憑一己之力奔向天涯海角!
然而,隨著我們逐漸熟悉這個遊戲,我們不禁懷疑:遊戲中的設定是否可能真實存在?為了揭開其謎底,我們便開始探究小恐龍的奔跑歲月!
貳、正文
主題一、小恐龍的身形與體態
眾所皆知,小恐龍是一隻暴龍。暴龍的學名是 Tyrannosaurus rex,在分類上為暴龍屬(Tyrannosaurus)目前唯一一個有效物種。
以最知名的暴龍化石——「蘇」為例,其身高(站立時垂直離地高)為 4.5 公尺。然而,考慮到並非每一隻暴龍的體型都相同,且小恐龍的站姿又與其他暴龍有相當的差異,我們希望能尋求更客觀的標準來測量其身高。
搜尋資料後, 我們發現以暴龍之前肢進行比較似乎是理想的選擇。維基百科中提到,每隻暴龍的前肢皆約 1 公尺長;另外在出土的成年暴龍化石中,其前肢化石長度皆大約為七十公分,加上軟組織後也將近一公尺長,我們便以此為基準來推測小恐龍的身高。

由上圖可發現,小恐龍的身高約為前肢長度的 9.98 倍,因此其身高為 9.98 公尺。 雖然在前階段得出了身高,但我們並無法從小恐龍的外貌推算出其體重,畢竟粗略地估計小恐龍有多少軟組織、組織有多厚、骨架有多重……顯然都會造成不可忽略的誤差。據此,我們決定以公認的暴龍平均體重── 9 噸,作為我們對小恐龍體重的假設。
主題二、身手矯健的小恐龍

我們疊合了小恐龍在平地奔跑以及起跳至最高點時的高度差,得到上圖,可發現小恐龍在跳到最高時,若一樣以前肢計算高度,則腳和地面的距離約為 20.8 m。為了以人類為標準,做出更精準的比對,我們令 K =( 跳高高度 / 身高 ),則可得到下表。

由此可見,幼童恐龍圖鑑中的龐然大物,其實擁有驚人爆發力! 此外,如果恐龍要達到 20.8 m 的高度,由位移公式 \( s=\frac{1}{2}at^{2} \) 可知 \( t=\sqrt{\frac{20.8}{0.5\times 9.8}}= 2.06s \)
則小恐龍起跳的初速度約為 0.5*2.06*9.81=10.1 m/s!
綜上,我們已經得知小恐龍起跳後可達到的高度與起跳之初速。小恐龍一躍而起後落地,從遊戲畫面中看不出落地所需要的緩衝時間,假設恐龍落地至靜止之時間為 0.01 s,若其動能完全轉換為落地時所受的正向力,根據牛頓第二運動定律,可知小恐龍的瞬間受力為 \( F=ma=9000\times (10.1/0.01)=9090000N \)
\( \Rightarrow 9090000N/9.81ms^{2}=926605kgw \)
以此推算,小恐龍優異的身體素質能使其背負約 103 位同伴。將成年人體重以 70kg 進行估算,則小恐龍更能夠承載 13237 名成人的體重!
主題三、小恐龍的移動速度
小恐龍遊戲是以遊戲得分作為計算遊戲進程的標準。然而,一分究竟代表幾公尺呢? 為解決單位換算的問題,以手機設定影片幀率 60FPS 並錄影,將影片匯入 tracker 程式,以先前計算出的恐龍身長作為基準,取遊戲得分 39 分的最後一幀影像與分數 42 分的最後一幀影像,測量恐龍與仙人掌的距離差。
結果可發現,在 39-42 分的過程中,恐龍距仙人掌的距離變化量為 35.39-7.85=27.54m。
由此可知,在小恐龍遊戲中每得一分,相當於使恐龍前進了 (27.54/3)=9.18m。
接著以遊戲分數 100 分為單位,測量小恐龍每移動 100*9.18=918 m 所需要的時間。最後以 v-t 作圖,可發現小恐龍遊戲在前 120 秒左右不斷加速,至 120 秒後,恐龍的速度趨為定值 160 m/s = 576 km/hr。
這個速度已是高速公路上車輛的 5 倍,甚至達到波音 747 飛行航速的一半!綜合前一主題所得出的結論,一隻能夠承載上萬名成人,速度又能超越高鐵的敏捷生物,無疑是作為陸上交通工具的優質選擇。

主題四、仙人掌的巨大阻礙
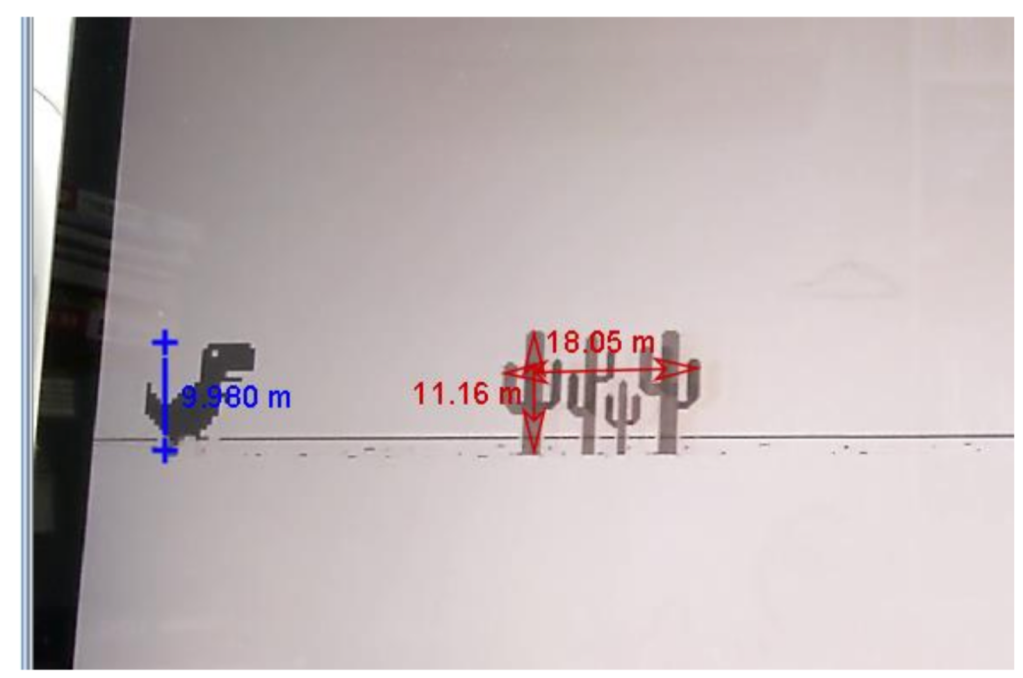
這張截圖中的四株仙人掌,囊括了小恐龍遊戲中所有出現的仙人掌的大小。以恐龍身 高 9.88 m 作為基準,可看到仙人掌叢中最高的仙人掌,高度達 11.16 m!
如此巨大的仙人掌究竟要在哪裡才找得到呢?經過查詢,美國與墨西哥西部的沙漠中,存在兩種巨型仙人掌:墨西哥巨型仙人掌(Pachycereus pringlei)與巨人柱(Carnegiea gigantea)。
墨西哥巨型仙人掌是目前記錄到植株最高的仙人掌,高度可達 19.2m。而巨人柱仙人掌得植株高度最高亦能達到 16m。將小恐龍的仙人掌外貌與前述二物種做比較, 我們認為遊戲中的品種較有可能是巨人柱(下左),因為墨西哥巨型仙人掌的分支在根部附近(下右),與遊戲中仙人掌分支較高的外貌不符。

主題五、天空中翱翔的巨獸
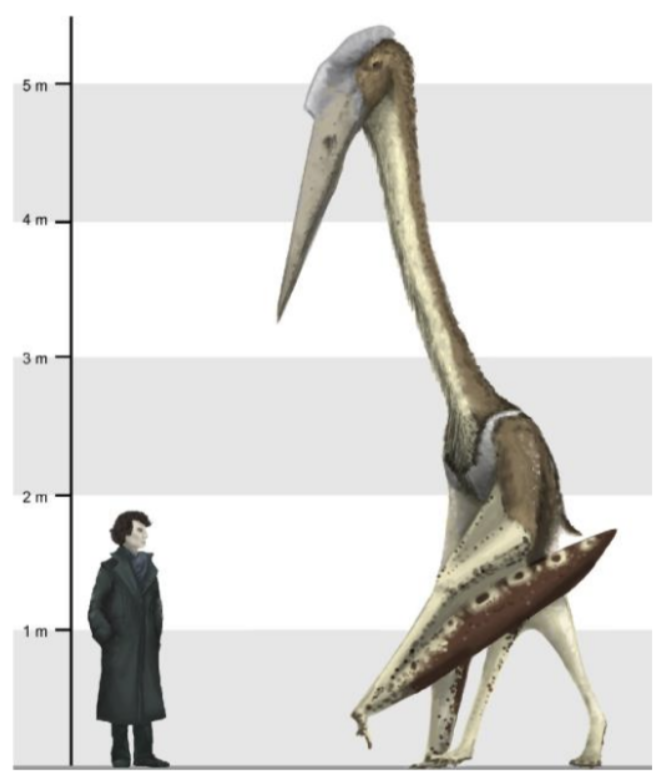
仿照主題四,以恐龍身高比對翼手龍體長,得到其體長為 10.20 m。我們經查詢發現白堊紀末期(小恐龍存在的時期),存在著翼龍目中已知最大的翼龍——阿拉姆波紀納龍 (Arambourgiania philadelphiae)。
根據網路上的假想圖,這隻恐龍不含喙長便有約 5 m。加上其約 2 m 長的喙,體長可能超過 7 m,已經接近小恐龍遊戲中翼手龍的體長。因此我們推測,遊戲中的翼手龍可能確實存在。
主題六、小恐龍所奔馳的時空
至此已經求得仙人掌與翼手龍的可能品種,我們便好奇遊戲中的物種有無可能出現在相同時空。
巨人柱的分布範圍在美國加利福尼亞州、亞利桑那州,以及墨西哥索諾拉州索諾拉沙漠(下圖左),暴龍主要分佈的範圍,在美國的西部地區與加拿大西南部(部分區域如下圖右),阿拉姆波紀納龍在美國一帶則可能有分布。
此外我們更發現,以上的生物在白堊紀末期都有存在的可能。綜合以上三個物種的分布時空,我們推測小恐龍遊戲中,恐龍應是奔馳在白堊紀的索諾拉沙漠一帶。
小恐龍作為網路世界中的虛擬遊戲,在 6500 萬年前的地球上,卻可能真實上演著!

參、結論
仔細分析了小恐龍遊戲後,我們得到以下結論:
一、遊戲的真實性
如主題六的討論,翼手龍、暴龍與仙人掌都有在同一時空存在的可能。不過遊戲中的翼手龍,其實是沒有隨著畫面移動的。換句話說,翼手龍在當地的強風吹拂之下,竟成了靜止於空中的運動狀態,此現象實在令人驚訝!
二、恐龍的存在,是利是弊?
6500 萬年前,廣闊的沙漠是小恐龍生活的絕佳地點。但時至今日,除了少數未開發的沙漠或人煙罕至的山地,人類社會恐怕沒有充足空間供牠活動了。若執意將小恐龍融入人類生活,考慮到其驚人的爆發力與實然上不「小」的身軀,牠勢必會對社會造成無法復原的破壞。
固執的人們若以特製圍欄將其囚禁,恐龍將失去自由奔馳的空間,更無法載著人類四處郊遊。21 世紀的我們,或許還是欣賞恐龍在 Chrome 世界奔馳的英姿即可。
參考資料