希維塔克·帕特爾(Shwetak Patel)為電腦協會計算大獎(ACM Prize in Computing)2018 年的得主,該獎項為電腦科學界僅次於圖靈獎的獎項,與費爾茲獎相同都有 40 歲以下的年齡限制,帕特爾獲獎時僅 37 歲。獲獎原因是帕特爾對於人類健康與永續生活,發展出創意與實用性兼具的感測系統。
帕特爾不僅擁有大學教授與創業家等多重身份,他還擁有合格的水工與電工執照。現為華盛頓大學計算機科學與工程和電氣工程的特聘教授,同時也是 Google 健康科技部門的執行長(Director of Health Technologies, Google)。他曾經創立過 Zensi家居能源監測公司(2010 年被 Belkin 公司收購),以及 Senosis Health 健康檢測公司(2017 年被 Google 收購)等。

接下來,就來介紹帕特爾改變世界並且獲得電腦協會計算大獎的研究!
智慧家居能源監測系統
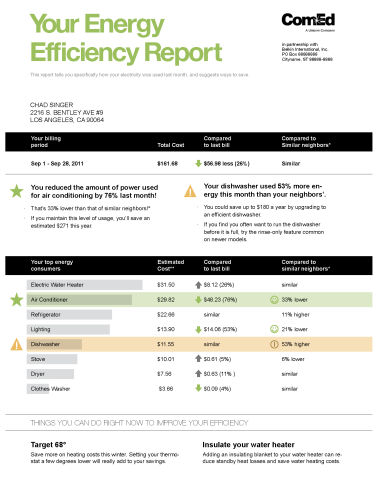
家家戶戶每個月收到帳單時,都知道家裡的用電量以及對應的費用,然而我們並不清楚是用在哪些方面。若是能收到每個月使用能源與用水的效率報告,就能夠讓人們了解自己的行為模式,進而採取行動增加能源效率與節省荷包。但是,要即時監控家居的能源消耗,一般來說需要裝設非常多感測器才可能辦到。
帕特爾成功發展出一套智慧家居能源監測系統,透過行動裝置就可以監控即時的耗電量與用水量。他發展的 ElectriSense 系統(用水則是 HydroSense 系統),利用既有的電路加上一個感測器(single plug-in device),就能把各種電器發出的高頻電磁干擾雜訊(high frequency EMI noise)當作訊號辨識對應的來源。
以iPad呈現建築物中每個電器即時的用電百分比
這套系統的發展,源自於複雜的電子交換特性與不同電器都會產生的雜訊,帕特爾藉此建立一套理論模型分析電器開關(稱為事件)的雜訊,並由使用者協助機器學習的程式訓練,最終發展出一套精確的預測系統。這套系統的精確度,甚至可以藉由輕微的公差來區分型號相同的電子產品。
考慮到感測器的易用性與持久性,帕特爾發展出可以維持 25 年、低耗電的無線感測系統與晶片(Sensor Nodes Utilizing Powerline Infrastructure, SNUPI),不需要經常替換非常方便。
更棒的是,一般人都可自行安裝,不需要專業的電工協助。未來這整套產品也可能推行至美國以外的地區,讓全球的家庭了解他們的詳細用電情況,進而改變人們的認知與行為,達成節約能源的永續目標。
用手機監測個人健康
人們通常要等到不舒服才會去醫院看病與檢查,過一陣子才會收到檢測報告,才被迫了解自己的身體狀況。現代的穿戴型裝置讓人們開始主動了解自己的健康狀態,除此之外,我們還有其他更好更深入的方法嗎?
帕特爾這幾年的研究領域包括了行動裝置於醫療上的應用。利用手機的 APP 與各種感測器監測個人健康狀態(personal health monitoring),在螢幕上就能立即看到結果,要進行定期與連續的監測也十分方便。
以 SpiroSmart 這個APP來說,它的操作非常簡單,不需要額外的硬體設施,只要對著手機裡的麥克風吹氣,手機會偵測受測者聲音裡的壓力波,自動轉換成即時圖形,就可以監控肺部功能是否衰退以預防慢性疾病。
像這類的檢測,傳統上一定要到醫院才能完成:受測者要對著肺量計 (spirometer)用力吹氣,以呼出的流速與容積(flow-volume)進行肺功能指標判讀。若偏離下圖的白色線段,便可能是這三種疾病的前兆,分別為哮喘 (Asthma)、囊腫性纖維化 (Cystic Fibrosis,CF)、慢性阻塞性肺病 (Chronic Obstructive Pulmonary Disease,COPD)。
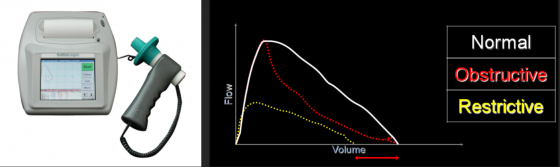
圖/帕特爾於海德堡桂冠論壇講座的投影片截圖
那麼,SpiroSmart 是怎麼做到類似的功能的呢?這跟一個「雜訊」有關:講話時會產生的聲道共振(vocal tract resonances)。過去數十年開發語音辨識演算法(speech recognition algorithms),都將聲道共振視為雜訊,希望盡量排除。但關鍵的地方就在這裡:聲道共振實際上與受測者呼出的氣流成比例關係。因此藉由聲帶的物理模型加上深度學習聲道共振的資訊,就能夠反推回受測者呼出氣體的流速─容積曲線。也就因此,用手機與麥克風就可以模擬肺量計了。
面對有人質疑手機APP的準確率,帕特爾表示 SpiroSmart 與原本價格 10 萬美金的肺量計相比的誤差為 5-10%,與美國食品與藥物管理署(FDA)對肺量儀的誤差容忍相同。表示技術上完全可以用手機 APP 取代醫院的儀器;然而要說服民眾相信一個 APP 可以是個醫療裝置,需要透過更多的科學教育與科學普及才有可能達成。
除了以上的案例,帕特爾的普及運算研究室還開發了許多醫療相關的手機 APP,像是以深度學習辨識咳嗽的CoughSense、把手指放在鏡頭前方檢測紅血蛋白(HemaApp)、在新生兒皮膚上放上色卡搭配鏡頭檢測黃疸(BiliCam)、利用陀螺儀檢測骨質疏鬆症(OsteoApp)等實用又創意的專案。
「你的雜訊就是我的訊號」 Your noise is my signal.
這句話貫穿了帕特爾的整個研究生涯,無論是從早期的智慧家居能源感測到近來的個人健康監測。這樣的創意是源自就讀喬治亞理工學院博士班時期,他花了許多時間進行許多跨領域的研究,當某個研究方法行不通的時候,卻有可能作為另一個研究的靈感來源與解決方案。因此把一般研究者亟欲排除的「雜訊」成為可辨識的「訊號」,突破既有知識的框架。

海德堡桂冠論壇小記與場邊觀察
帕特爾以電腦協會計算大獎得主的身份,於 2019 年首次參加海德堡桂冠論壇(Heidelberg Laureate Forum, HLF),也是論壇史上最年輕的得主,非常受到歡迎。每天都忙著接受採訪與分享自己的經驗,幾乎無時無刻不被一群學生包圍發問。
對帕特爾而言,海德堡桂冠論壇是個非常獨特的盛會,在這裡能夠一次見到背負盛名因此平時難以見到的大師,以及從前輩的身上了解到得主如何對世界產生長期影響,是個前所未有的經驗。
即使已經身為得主,帕特爾認為如果他年輕的時候有機會參與論壇,會對早期的學術生涯更有幫助,同時也希望讓更多年輕研究者知道這個世界級的活動,讓與會者覺得能夠脫穎而出參與論壇是個殊榮。(註:2019年海德堡桂冠論壇有800名年輕研究者報名,最終錄取200名)

圖/Heidelberg Laureate Forum
從小時候動手作到學術遊樂場
帕特爾出生於美國阿拉巴馬州的塞爾瑪(Selma, Alabama),擁有高學歷的父母自印度移民至美國,經營一間含有數十個房間的汽車旅館。因此,帕特爾從小是在汽車旅館旁的公寓長大,就像是旅館的管理人員,必須做一些庶務像是整理床位以及修理壞掉的燈泡,甚至是維修自動販賣機,自然而然對於動手作(tinkering)十分熟悉。
習慣動手作,也讓他的學術研究變得與眾不同。帕特爾在博士班就發表了很多篇與感測器有關的論文,包括機器學習、永續、醫療等領域,並開始創立自己的公司。他同時是實踐家、發明家、會寫論文。思考未來的職涯發展時,認為大學教職可以是個自由研究的遊樂場,可以讓電腦科學變得有影響力,因此選擇成為大學教授。
與一般教授不同的是,與其研究如何增進 1% 演算法效率,他認為不如去思考如何動手開發出一個對人類有直接影響的產品,能夠正向影響數百萬人的想法甚至行為,其意義會超過發表許多論文與獲得終身教職。
對一個應用導向的研究者來說,開發產品才能夠真正到影響一般民眾。帕特爾與其團隊通常把產品開發到一個程度,就讓其他人收購公司去加速產品的開發,接著投入下一個研究。
即使從研究生時期就被其他人開始質問是否不務正業,例如:「你不是個電腦科學家、你沒有一個專精的領域、你不會拿到教職」,然而擁有自由探索的學術遊樂場對他來說是最自在的。

圖/Heidelberg Laureate Forum
選擇學生條件與社會服務
要怎樣才能進入帕特爾的學術遊樂場一起玩呢?帕特爾強調,選擇學生的時候他最重視的是善良(kindness)與否,一方面是若對人不友善就會很難找到合作對象,尤其研究室關注的領域與醫療保健與永續相關,關注其他人是必要條件。畢竟技術可以透過學習而來,然而人格特質不容易改變。
那麼,帕特爾是如何指導學生的呢?在研究室裡,有很多不同領域的人,像是電腦科學、電子工程以及醫療背景,帕特爾會試著創造出每個人都貢獻己力才能解決的專案,讓跨領域合作自然而然發生。另外,與其安排好研究方向與每一個細節,帕特爾傾向激勵學生、與學生討論研究的大方向、留給學生探索的空間。
帕特爾從高中時期就有機會接觸研究,因此大學時期也較同儕來得早開始寫論文,而這徹底改變了他的研究生涯,他自認非常幸運。因此,他希望現在的高中生能早點接觸研究,因此特別為高中生開放了 8-10週的暑期研究室實習,期待能夠開啟學生對於程式與科技的想像。
值得一提的是,帕特爾近來婉拒至知名大學演說,他傾向把時間留給郊區的學校,接觸更多高中以下的學生;此外,他認為傳遞科學知識最有效率的是為第一線的教師上課,讓教師在課堂分享電腦科學是個很強大的工具,能夠對社會有正面影響,電腦科學不是只有電玩遊戲。

讓世界變得更好的人文精神:給年輕研究者的建議
「我的研究社群是整個世界與人類。」
帕特爾在海德堡桂冠論壇的演說,除了介紹行動裝置於健康的應用之外,還提供建議給年輕研究者。他提到這是個特別的時代,人類史上擁有最多工具(如人工智慧、資料分析與視覺化)、跨領域研究非常興盛;最好的提問與答案,都在不同領域的交會之處。
當帕特爾還是個年輕教授時,常常被問到「你是什麼領域?是網路、系統或資料庫?」同樣地,許多年輕研究者內心假設「我必須成為一個數學家,必須是個電腦科學家,必須研究某個單一領域」。
然而這並不是世界運作的方式,年輕研究者當然可以在某個領域創新,但是別忘了跳出領域的框架,思考像是政治與政策等更廣的層面,以及自己在做的事對於人類與世界是否有深切的影響。
假使年輕研究者只是想著要拿諾貝爾獎、圖靈獎等大獎,這樣的心態(mindset)本身就是個災難,若是找到自己有熱情的事物,而且每天醒來都為此感到興奮,並且奮力地驅策自己前進,將有最佳的機會能夠邁向成功。
希維塔克·帕特爾在他的研究生涯,實踐了科學與工程最重要的價值──人文精神。
延伸閱讀:
- 華盛頓大學普及運算研究室:Ubicomp Lab – Ubiquitous Computing Lab at the University of Washington
- 海德堡桂冠論壇專訪影片:The Heidelberg Laureate Forum Foundation presents the HLF Portraits: Shwetak N. Patel
- 海德堡桂冠論壇講座影片:New Ways of Thinking the Mobile Phone for Healthcare (52 mins)與投影片
- 屬於數學與電腦科學的榮耀,聚集大師的海德堡桂冠論壇
想親炙海德堡桂冠論壇,與大師們面對面交流嗎?
每年11-隔年2月開放來自全球的年輕研究者報名
詳情可上官網: https://www.heidelberg-laureate-forum.org/