文/蔡天新,本文摘錄自《數學的故事》,2019年時報出版
風格即人。
寫作能力包括思想、感覺和表達,內心的明晰,味覺和靈魂。——布豐
投擲小針的實驗
十八世紀某日,法國博物學家布豐(Comte de Buffon)邀請了許多朋友來家中做客,席間一起做了個實驗。布豐先在桌上鋪好一張大白紙,白紙上畫滿了等距離的平行線,再拿出很多等長的小針,小針的長度剛好是相鄰平行線間距的一半。布豐說:「請大家隨意把這些小針往白紙上扔!」客人們紛紛照他所說的做。
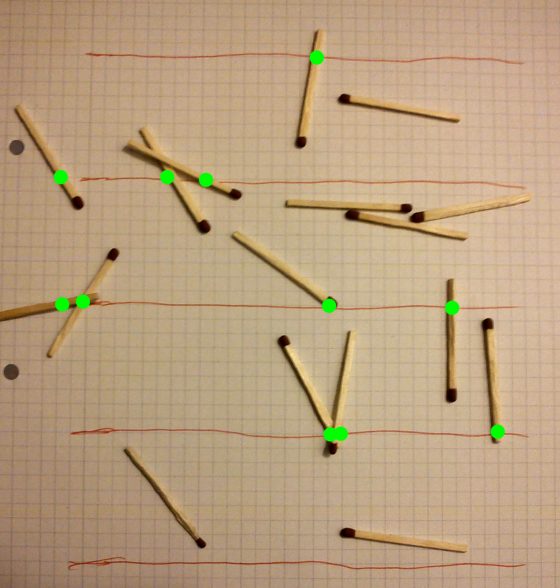
他們總共投擲了二千二百一十二枚小針。統計結果表明,與紙上平行線相交的有七百零四枚,2210÷704≈3.142。布豐說:「這是 π 的近似值。每次實驗都會得到圓周率的近似值,而且投擲次數愈多,求出的圓周率近似值就愈精確。」這就是著名的「布豐實驗」。
布豐發現,如果選用的小針長度固定,那麼有利扔出(扔出的針與平行線相交)與不利扔出(扔出的針與平行線不相交)的次數之比,就是一個包含 π 的運算式。特別的是,如果小針的長度是平行線距離的一半,那麼有利扔出的概率恰好為 1/π。
布豐投針問題的實驗數據
下面是利用這個公式,用概率法獲得圓周率近似值的歷史資料。
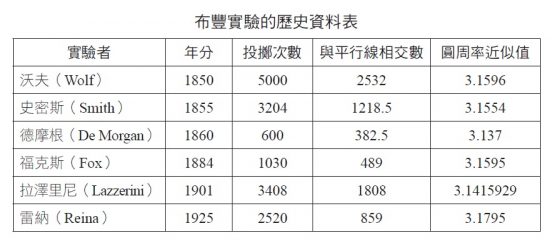
其中,義大利人拉澤里尼在一九○一年投針三千四百零八次後,得出的圓周率近似值為 3.1415929,精確到小數點後六位。只不過他的實驗資料遭到了美國猶他州韋伯州立大學的巴傑教授的質疑。但無論如何,透過幾何、概率、微積分等不同領域和多種管道均可求取 π 的值,這仍然令人驚訝。
布豐投針實驗是第一個用幾何方式來表達概率問題的例子,也是首次利用隨機實驗來處理確定性的數學問題,它推動和促進了概率論的發展。
布豐投針問題的證明
找一根鐵絲做成圓圈,使其直徑恰好等於兩條平行線的間距 d。不難想像,對於這樣的圓圈來說,不管怎麼扔,都會與平行線有兩個交點。這兩個交點可能在一條平行線上,也可能在兩條平行線上。因此,如果投擲圓圈的次數為 n,那麼交點總數必為 2n。
現在把圓圈打開,變成一根長度為 πd 的鐵絲。顯然,這根鐵絲投擲後與平行線相交的情形要比圓圈複雜,共有五種情況:四個交點,三個交點,兩個交點,一個交點,無交點。
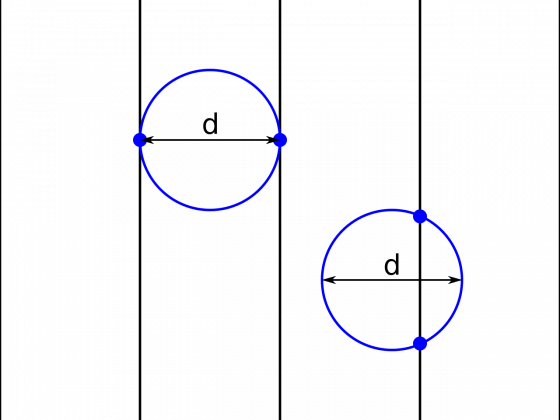
由於圓圈和直線的長度同為 πd,根據機會均等原理,當投擲較多次且投擲次數相等時,兩者與平行線交點的總期望值應該是一樣的。也就是說,當長度為 πd 的鐵絲被投擲 n 次時,與平行線的交點總數也應該約為 2n。
現在來討論鐵絲長度為 l 的情形。隨著投擲次數 n 的增加,鐵絲與平行線的交點總數 m 應當與長度 l 成正比,因而有 m=kl,其中 k 是比例係數。
為了求出 k,考慮到當 l=πd 時的特殊情形,有 m=2n。由此可得
\( k= \frac{2n}{\pi d} \)
代入上式 (m=kl),有
\( \frac{m}{n}= \frac{2l}{\pi d} \)
特別地,取 l=d/2,便可得到布豐的結果,即 m/n=1/π。這個證明多多少少比較直觀,若學了高等數學,還可以用概率論和微積分的方法提出更嚴格的證明。
布豐,身兼多職的皇家植物園園長
有趣的是,布豐的名字與義大利尤文圖斯守門員兼義大利足球隊隊長布馮的名字拼法相同,均為 Buffon,只不過前者是法國人,後者是義大利人;前者生活在十八世紀,後者則與我們同年代。
布豐出生於盛產美酒的勃艮第小官吏之家,母親頗有人文修養。他十六歲時前往第戎的學院讀書,雖然喜歡數學,卻不得不遵從父命學習法律。此番經歷與他的同齡人、瑞士數學家歐拉相似,那會兒歐拉在離第戎不遠的巴塞爾大學,聽從父親之意攻讀神學和希伯來語。
原因在於,對於非顯貴家庭出身的年輕人來說,牧師、醫生和律師不失為安身立命的三個好職業,歐拉卻偏偏對數學情有獨鍾。
歐拉二十歲時隻身前往俄國的聖彼得堡科學院,先在醫學部,後來轉到數理學部,憑藉自己的鑽研和努力,成為十七世紀最偉大的數學家,也被譽為歷史上最偉大的四位數學家之一。布豐同樣是在二十一歲時,轉往法國西部的昂熱大學攻讀醫學、植物學和數學,並結識了一位在歐洲大陸旅行的英國公爵,陪他去了不少地方,也多次隨他前往英國,後來還成為英國皇家學會會員。

二十五歲時,布豐的母親去世,他回到故鄉經營自家農場。他經常去巴黎,是文學和哲學沙龍的常客,並結識了伏爾泰等知識分子,自己也著作等身。他認為,寫作能力包括思想、感覺和表達,內心的明晰,味覺和靈魂。布豐在四十六歲那年當選為法蘭西學院院士,就像二十世紀的數學天才龐加萊(Henri Poincaré),同時站在科學與人文兩大領域的頂峰。
布豐三十二歲時被任命為巴黎皇家植物園園長,直到去世都擔任此職。他致力於把植物園辦成學術和研究中心,從世界各地購買或獲取新的植物和動物標本。布豐翻譯過英國植物學家黑爾斯(Stephen Hales,第一個測量血壓的人)的《植物志》(Vegetable Staticks)和牛頓的《流數法與無窮級數》(Methodus Fluxionum et Serierum Infinitarum),並探索了牛頓和萊布尼茨發現微積分的歷史過程。布豐還主編巨著《自然史》,原計畫出五十卷,在他去世前出了三十六卷。
布豐生前以博物學家的身分和自然史方面的著作聞名,並以「風格即人」的理念為人稱道和傳世。這就像北宋的政治家沈括,因為寫了《夢溪筆談》而被公認是偉大的博物學家,在數學、物理學、地質學等方面同樣卓有成就。布豐的興趣也非常廣泛,且在多個領域均有重要建樹。
布豐是最早提出要將地質史按照時期劃分,並發表太陽與彗星碰撞產生行星此一理論的人。他還率先提出物種絕跡說,促進了古生物學的研究。不過,他說新世界(指美洲)的物種之所以不如歐亞大陸,缺乏大型和強大物種,男子氣概的人也少於歐洲,是因為美洲大陸沼澤的氣味和茂密的森林,大大激怒了湯瑪斯.傑佛遜(Thomas Jefferson),派出二十個士兵去新罕布夏州森林尋找公鹿,好向布豐展示「美國四足動物的雄壯和威嚴」。
布豐四十五歲時娶了一位來自故鄉沒落貴族世家的小姐,他們的第二個孩子倖免夭折,五年後卻面臨母喪,布豐又在他八歲時病重,幸好隔年病情就好轉,從此父子平安無事。布豐後來活到八十一歲,晚年當選為美國藝術與科學學院的外籍院士。
蒙地卡羅方法是什麼?
如同前文提到的布豐投針試驗,透過概率實驗的方法來估計某一個隨機變數的期望值,這樣的方法被稱為蒙地卡羅方法。

蒙地卡羅是全球馳名的賭城,位於法國國界內離義大利不遠的摩納哥,傍依地中海海濱,屬於風景如畫的「蔚藍海岸」一部分。奧斯卡電影《蝴蝶夢》曾在這裡取景,一級方程式賽車在這裡也設有一站。我年輕時遊歷此地,發現它與美國的拉斯維加斯和大西洋城不同,要求客人西裝革履,穿短褲或拖鞋者謝絕入內。
蒙地卡羅方法是美國在二戰期間執行研製原子彈的「曼哈頓計畫」時提出來的,主要歸功於波蘭人烏拉姆(Stanislaw Ulam)和匈牙利人馮.諾依曼這兩位猶太籍數學家。馮.諾依曼以賭城蒙地卡羅之名為此方法命名,也為它罩上了一層神祕面紗。其實在此之前,蒙地卡羅方法就已存在,比如布豐實驗。
如今,蒙地卡羅方法在原子物理學、固態物理學、化學、生態學、社會學與經濟行為學等領域均獲得廣泛應用。下面,我們再舉兩個例子。
例一:把布豐實驗做個推廣,利用鈍角三角形的邊長計算圓周率。

任意給三個正數,以它們為邊長,可以圍成一個鈍角三角形的概率 P 也與 π有關,這個概率為(π–2)/4。證明如下:
設這三個正數為 x、y、z,而且 x≦y≦z。對於每一個確定的 z,考慮到一個三角形任意一邊的長度小於另外兩邊的長度之和,故滿足
x+y>z, x2+y2<z2
後一個不等式成立是因為鈍角三角形和畢氏定理。我們很容易證明,這兩個不等式即為以這三個正數為邊長可圍成鈍角三角形的充分必要條件。
因此,滿足假設條件的(x, y)的可行區域為直線x+y=z 與圓 x2+y2<z2 所圍成的小弓形,而(x, y)的總可行區域為一個邊長為 z 的正方形。這樣一來,以三個正數為邊長可以圍成一個鈍角三角形的概率為
由此可見,這個概率與 z 的選取無關。因此,對於任意正數 x、y、z,均有 P=(π–2)/4,命題得證。
為了估算 π 的值,我們得透過實驗來估計其概率,過程可交由電腦程式設計來實現。事實上,x+y>z,x2+y2<z2等價於(x+y–z)(x2+y2–z2)<0,因此只需檢驗後一個不等式是否成立即可。
若進行了 m 次隨機實驗,有 n 次滿足該不等式,那麼當 m 夠大時,n/m 會趨近於 (π–2)/4。而若令 n/m=(π–2)/4,可求得 π=4n/m+2,由此即能估計出 π 的近似值。
例二:利用蒙地卡羅方法,求任意曲邊梯形的池塘面積。
蒙地卡羅方法的基本概念是:先建立一個概率模型,使所求問題的解正好是該模型的參數或其他相關的特徵量。再透過模擬某個統計實驗,即多次隨機抽樣實驗(確定 m 和n),統計出該事件發生的百分比。只要實驗次數夠多,該百分比便近似於事件發生的概率,這其實就是概率的統計學定義。
可以說,蒙地卡羅方法屬於實驗數學的一種。它的適用範圍很廣泛,既能求解確定性的問題,也能求解隨機性的問題,甚至可以探索科學研究中的理論問題。
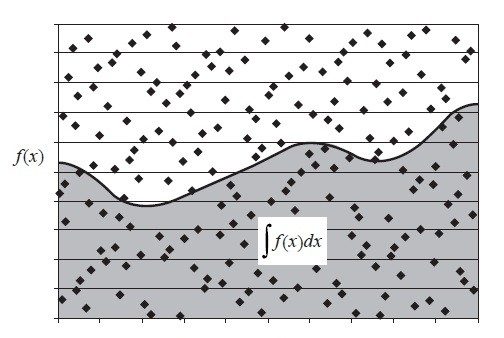
例二告訴我們,如何利用蒙地卡羅方法近似計算定積分,這屬於數值積分問題。那麼,任意曲邊梯形形狀的池塘面積,應該怎樣測算呢?
設計方案是:如下圖所示,假定池塘位於一塊面積已知的矩形農田中央,隨機朝農田扔泥巴,泥巴可能會濺起水花(落在池塘內),也可能不會(落在池塘外)。估計「濺起水花」的泥巴數占總泥巴數的百分比,便可根據該比例和農田面積近似算出池塘的面積。