- 簡麗賢/北一女中物理教師
「十二年國民基本教育課程綱要」將在 2019 年 8 月 1 日正式上路,新課綱的核心素養揭櫫「系統思考與解決問題」與「符號運用與溝通表達」,在學習表現項目中強調「科學的態度與本質」,期望能培養學生應用科學思考與探究的能力。
新課綱重點:跳脫框架,加強思考與提問
筆者曾讀過一則印象深刻的幽默短文,聯合國出一道題目給全世界的小朋友回答:「對於其他國家糧食短缺的問題,請你提出自己的看法。」非洲的小朋友看完題目後,不知道什麼是「糧食」;拉丁美洲的小朋友不知道什麼是「請」;英國、法國的小朋友不知道什麼是「短缺」;美國的小朋友不知道什麼是「其他國家」;而臺灣的小朋友不知道的,是「自己的看法」。
雖然這只是一則網路短文,然而臺灣追求標準答案卻是不爭的事實。思考和探究是培養科學素養的二部曲;符合標準答案卻少了自己的看法,是新課綱教學值得省思的課題。
韓愈在〈進學解〉提到「行成於思,毀於隨。」《論語》則說:「學而不思則罔,思而不學則殆。」強調讀書和行動都要能思考,而不是跟隨別人。以高中物理課程教學為例,引導學生了解定律的內容及其侷限性、思考物理學家的理論與實驗或能探究生活中的現象,這些都比標準答案更重要。
儘管十二年國教的必修時數減少,教師教學時,仍需引導學生澄清物理概念,鼓勵學生多思考多提問。從思考和提問中解惑,學得更多,更能建立深厚的科學概念。
適當融入趣味題材,激發學習創意

筆者在課堂教學中,常以提問引起學生學習的動機,融入升學考試的題目轉化成問題,刺激學生思考。此外,也藉此同樣的主題,引導學生提出疑惑,呼應新課綱溝通互動的核心素養面向。以 108 學年度學測試題為例,修改後成為教師提問與學生思考的素材:
某科幻小說中的情境曾提及,月球公轉方向與現在相反,但公轉速率不變。如果此情境為真,其他影響潮汐變化的因素亦不改變。回答下列問題:
- 月亮會自西方升起,東方落下嗎?
- 月亮每天會提早約50分鐘出現嗎?潮汐的時間是否也改變呢?
回答以上問題,必須具備地球自轉、月球繞行地球公轉和牛頓萬有引力的概念。潮汐是地球受到太陽及月球的重力與地球、月球間運動的交互作用造成引潮力的結果,因月球距離地球較太陽距離地球近,因此潮汐變化受月球引力的影響較大。月球從地平線東方升起,西方落下是地球自轉造成的現象,與月球公轉方向無關,故月球仍然從地平線東方升起,西方落下。月球繞地球公轉方向與地球自轉相同,潮汐變化時間與月球位置有關。
依據高中教材,月球公轉地球 1 圈 360 度,以朔望月 29.5 天計算,月球公轉 1 圈後,因地球同時自轉,月球出現在天頂位置時會比前一天延遲大約 360÷29.5÷360×24×60=48.81 分鐘,也就是翌日的月升月落和滿潮時刻都會比前一天延遲約 50 分鐘。若其他影響潮汐變化的因素都不變,而月球公轉地球的方向相反,則月升月落及潮汐現象變成每日提早 50 分鐘。
儘管這是科幻小說出現的情節,卻是延深思考和科學推理的提問素材,引導學生思考和畫圖,提出自己的看法,培養科學素養。
加入生活情境,文字、圖像輔助答題
又如 108 學年度學測的題組題,亦是教師提問的好題材:
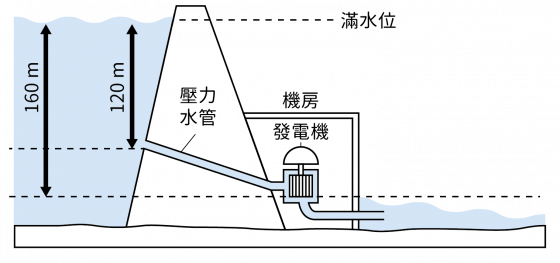
一座水庫的蓄水量與從壩底算起的水位關係如表所列,水位 250 公尺時為滿水位。在滿水位下方 120 公尺處,設置壓力水管將水引入發電機,進行水力發電,發電機位於滿水位下方 160 公尺處,如圖所示,且越接近壩底,水壩的厚度越厚。(重力加速度 g 為 10 m∕s2,水的密度為 1.0 g∕cm3)
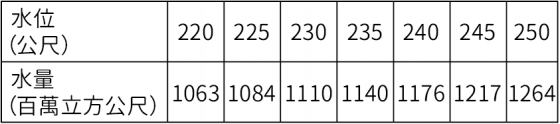
水庫水位與蓄水量
- 依據圖中所示的水力發電設計,就能量轉換的觀點是哪些能量形式的轉換?
- 滿水位時,水庫水面的面積最接近多少百萬平方公尺?
- 已知發電廠設計的水流量為 30 m3∕s ,若本發電裝置僅可將水力所提供能量的轉換為電能,且水庫在維持滿水位情況下發電,則本發電廠的最大發電功率約為多少 MW?
回答上述的提問,必須根據能量形式、水的密度單位轉換、功率定義及力學能守恆的先備知識。
- 第一小題的參考答案為水的重力位能轉換成動能,再轉換成電能。
- 第二小題討論滿水位時,水庫水面的面積最接近多少百萬平方公尺,關鍵詞有滿水位、水面的面積最接近等。且提供的數據中,水位自 245 公尺升高至滿水位 250 公尺,水位差 ΔH=250-245=5 公尺,水量差ΔM=1264-1217=47 百萬立方公尺,故水面的面積最接近 A=△M∕△H=47∕5=9.4 百萬平方公尺。
- 第三小題討論發電廠設計的水流量再維持滿水位時,發電裝置僅可將水力提供的能量進行 25%轉換,同時要注意題目的最大發電功率約為多少。上述的關鍵句若僅聚焦高中生學測命題範圍內的力學能守恆,可說明如下:最大發電功率發生在滿水位時,水流量為 30 m3∕s,重力位能完全轉換後的 25%轉換成電能。依據題意知道,重力加速度 g 為 10 m∕s2為 1.0 g∕cm3水的密度換算單位為 1.0×10-3∕10-6=103 kg∕m3,且題目又說明水流量為 30 m3∕s,相當於每一秒水的質量為 m=體積×密度= 30 m3∕s×103 kg∕m3=3.0×104 kg。滿水位至發電機位置的高度差 Δh 為圖中的 160 公尺,每一秒水的重力位能變化 ΔU=mgΔh=3.0×104×10×160 焦耳,故轉換成電能僅 25%轉換,功率為 3.0×104×10×160×25%=12×106 瓦特,亦即12 百萬瓦特(MW)。
上述說明是升學考試命題範圍內的高中課程內容,僅為閱卷需要的參考答案作考量,或許學生或物理教師會有不同的想法。就命題設計而言,應是呼應素養命題原則,素材引用生活情境,命題設計情境化,評量考生的整合運用能力,考察考生是否能夠整合運用知識,綜合閱讀理解、邏輯推論與圖表判讀等能力。
就考生回答問題的困難度而言,推測回答第二題時,可能直接引用表格最後一格數據,以水量和水位的數據相除,得到滿水位時的水面表面積,這樣的直觀不算合理,因為水庫並不是立方體或圓柱體,而且越接近水庫底部壓力越強,水壩結構需越厚。思考題意,看到「滿水位」的關鍵詞句,合理觀點應看表格最後 2 格的數據,再以水量差除以水位差得到最合理答案。
第三題可能困在「發電廠的最大發電功率」的定義以及水的密度如何換算。考生很可能採用 120 公尺和 160 公尺的數據,以兩者數據差代入 ΔU=mgΔh,並且乘以 25%得到 3 MW,卻不是正確答案。若單純依據力學能守恆,最大發電功率是重力位能完全轉換後,乘以 25%後得 12 MW,即找到答案。
上述命題和參考答案,畢竟侷限於升學考試題目;然而引入教學思考與提問,或許可以聽到學生多元想法和見解,針對學生的疑惑、盲點和迷思,甚至獨特看法,都可能激盪出更多的教學思維。從學測試題找出思考與提問的素材,是教師教學的可行方向。
〈本文轉載自《科學月刊》2019年3月號〉
一個在資訊不值錢的時代中,試圖緊握那知識餘溫的科普雜誌。